時間測度上Lotka－Volterra競爭模型的周期解

張 青，張 昆

（安徽農業大學理學院，安徽合肥230036）

近年來，關于連續型和離散型捕食系統的周期行為的研究吸引了諸多學者的關注．但在時標上研究捕食系統的周期解的相關工作不多．時標動力學方程作為一種更為廣泛的方程類型，它包括了微分方程和差分方程作為特例，是近年新興的研究領域．自2006年Bohner等［5]首次運用重合度理論中的延拓定理研究時標動力學方程的周期解存在性以來，相繼有些學者進行了此類問題的研究．經典的Lotka－Volterra競爭模型可表示為

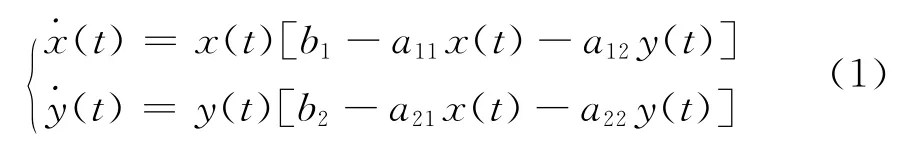
這里x（t）和y（t）分別表示食餌和捕食者的密度，b1和b2分別表示兩種群的內稟增，bi，aij（i，j＝1，2）均為正常數，其具體意義可見文獻［9] ．考慮到環境的變化，我們得到更適合的Lotka－Volterra競爭模型

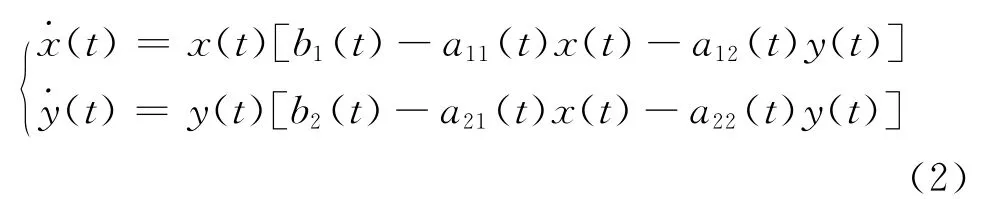
本文將在時標上研究如下系統

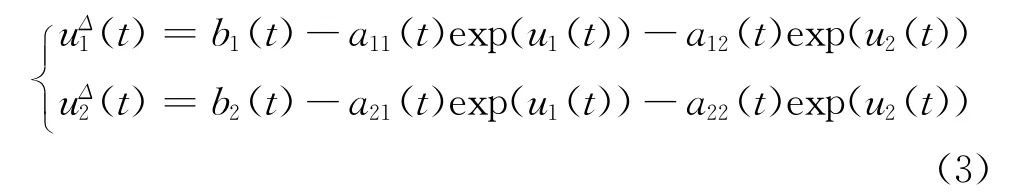
的周期解存在性問題．令x（t）＝exp（u1（t）），y（t）＝exp（u2（t）），當T＝R時，系統（3）變成（2）．T＝Z（整數集）時，系統（3）變成

1 基本引理

為了證明周期解的存在性，先介紹重合度理論中的連續性定理．設X，Z是賦范向量空間，L：DomL?X→Z為線性映射，N：X→Z為連續映射．如果DimKerL＝codim ImL＜＋∞且ImL為Z中的閉子集，則稱映射L為指標為0的Fredholm映射．如果ImL是指標為0的Fredholm映射且存在連續投影P：X→X及Q：Z→Z使得lmP＝KerL，ImL＝Ker Q＝Im（I－Q），則L（I－P）X→ImL可逆，設其逆映射為Kp．設Ω為X中的有界開集，如果有界且Kp（I－Q）N→X是緊的，則稱N在為L－緊．又因為ImQ與Ker L同構，所以存在同構映射J：ImQ→Ker L．

引理1［10]（連續性定理）設L是指標為0的Fredholm映射，N在為L－緊的．假設：（a）對任意的λ∈（0，1），x∈?Ω，都有LxλNx；（b）對任意的x∈?Ω∩Ker L并且deg｛JQN；Ω∩Ker L；0｝0，則方程Lx＝Nx在DomL∩內至少存在一個解．

引理2［11]設t1，t2∈Iω，t∈T，若g是T→R的ω－周期函數，則

2 主要結論

定義1 lω＝｛（u1，u2）∈（T，R2）：ui（t＋ω）＝ui（t），i＝1，2，?t∈T｝且

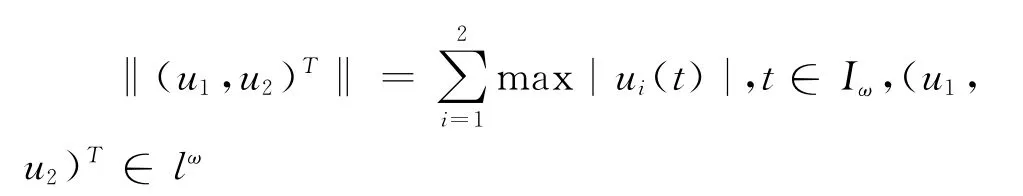
顯然lω是Banach空間．

證明 令X＝Z＝lω，定義

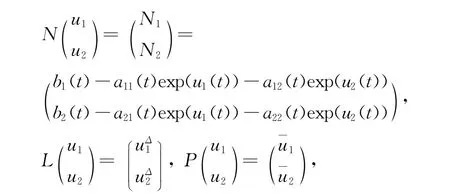
設Ω是X中的有界開集，顯然QN和Kp（IQ）N是連續的．因為X是Banach空間，所以由Arzela－Ascoli定理知在Ω上是緊的，且QN）是有界的，于是N在上是L－緊的．

考慮算子方程Lx＝λNx，λ∈（0，1）即

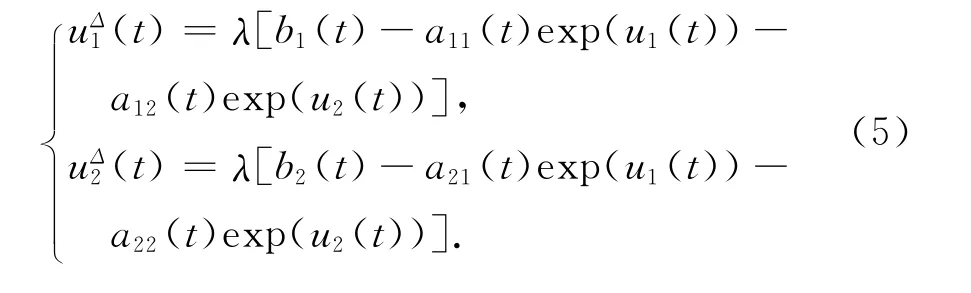
設（u1（t），u2（t））T∈X是式（5）對應某個λ∈（0，1）的一個解，在［k，k＋ω] 對式（5）積分得

由式（5）～式（7）得

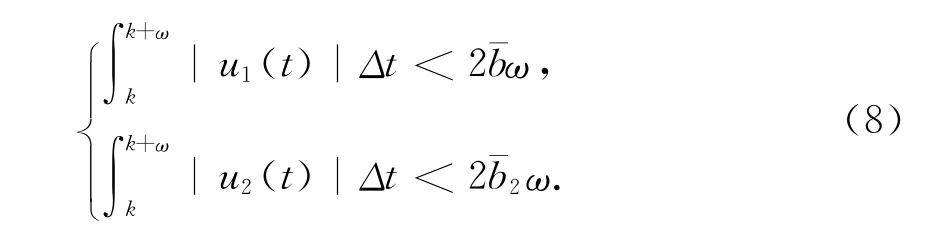
因為［u1（t），u2（t）]T∈X，所以存在ξi，ηi∈［k，k＋ω] （i＝1，2）使得

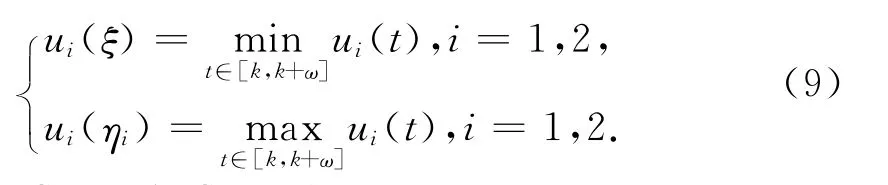
由式（6）和式（7）得

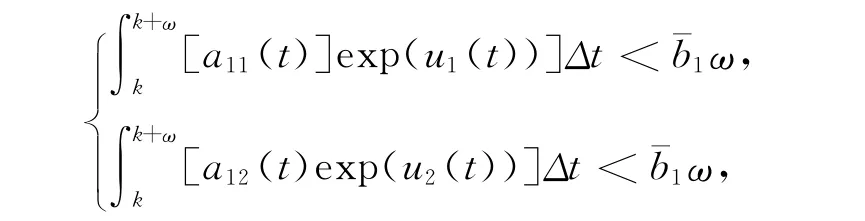
于是

下面考慮兩種情況．

（I）若u1（η1）≥u2（η2）則由式（6）得

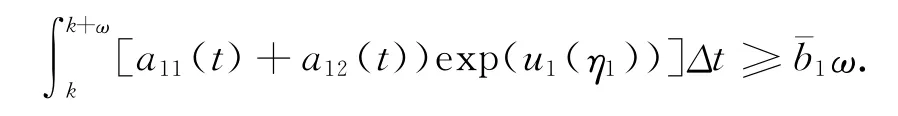
因此

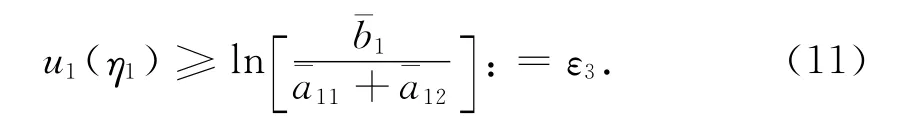
由式（8），式（10）和式（11）得

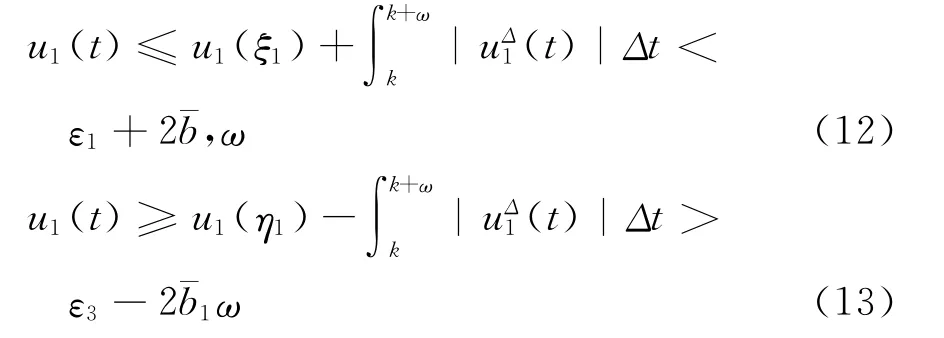
所以

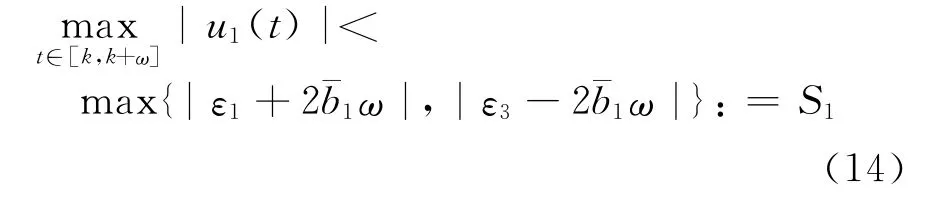
根據式（6）我們知道

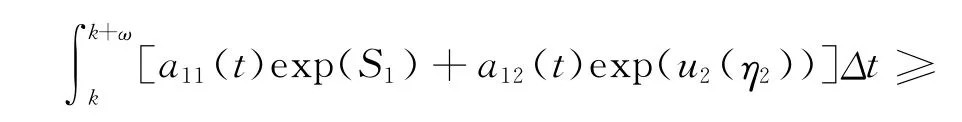
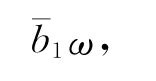
于是

由（8），（10）和（15）得

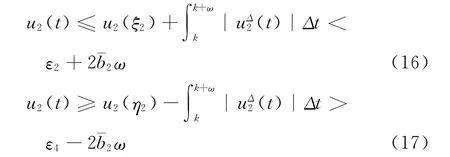
所以

（II）若u1（η1）＜u2（η2）則由式（6）得

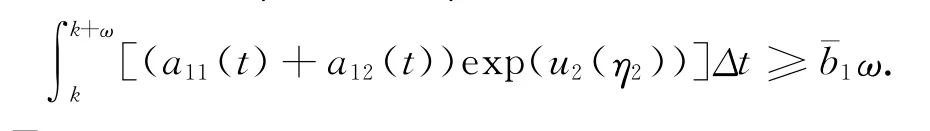
于是

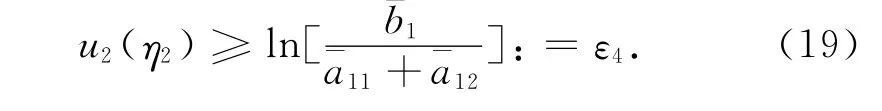
由（8），（10）和（19）得

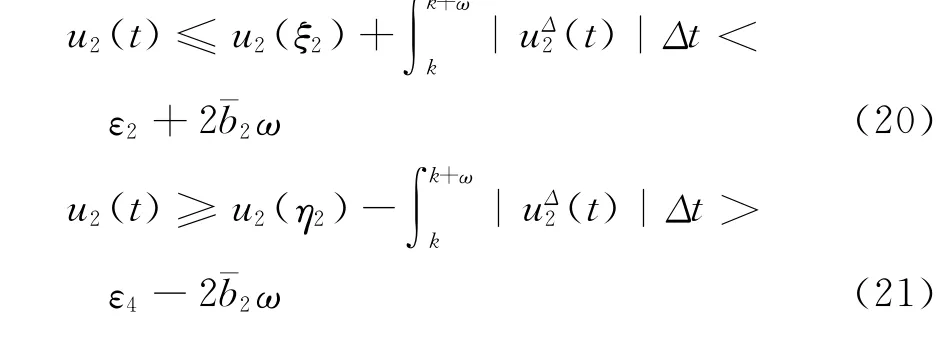
所以

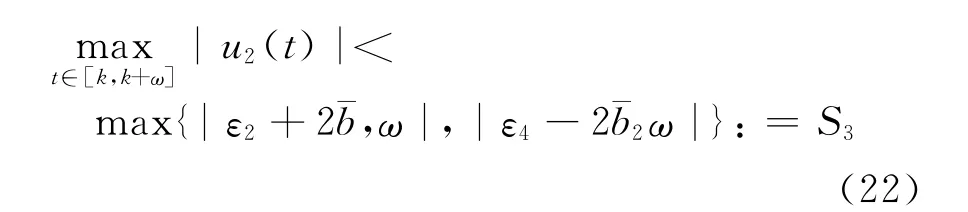
根據式（6），我們知道

于是

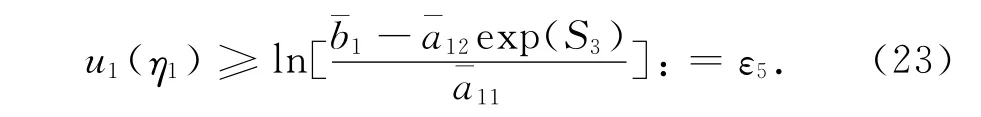
由（8），（10）和（23）得

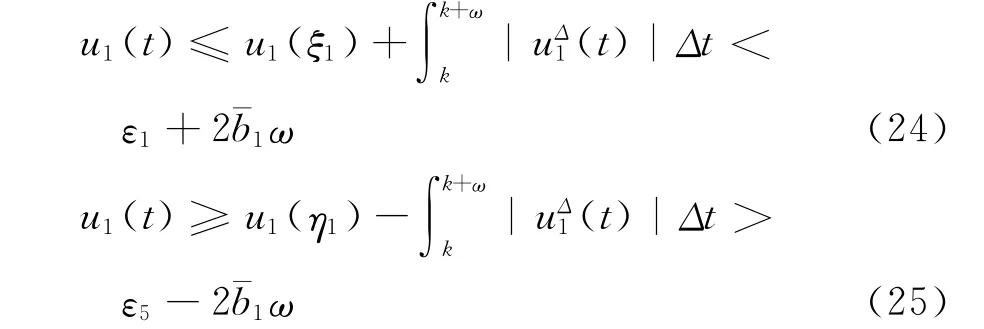
所以

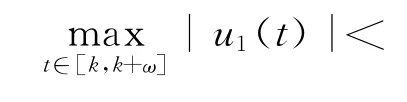
顯然Si（i＝1，2，3，4）的取法與λ無關．記S＝max｛S1，S4｝＋max｛S2，S3｝＋S0其中S0為充分大的數，使得下面的代數方程組

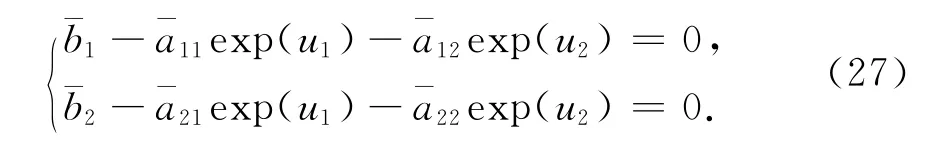
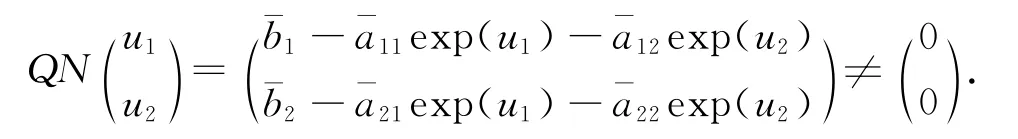
如果方程組（27）無解，顯然有

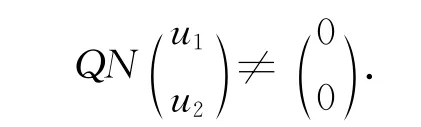
定義2 φ：DomL×［0，1] →X：

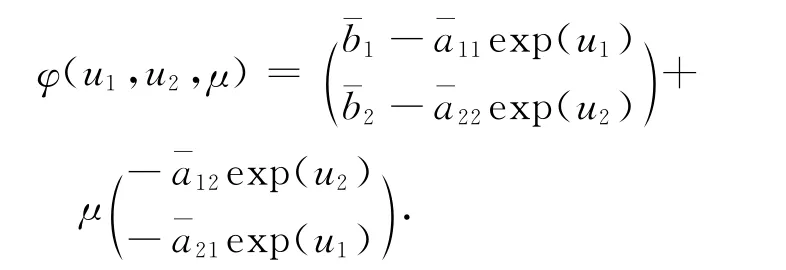
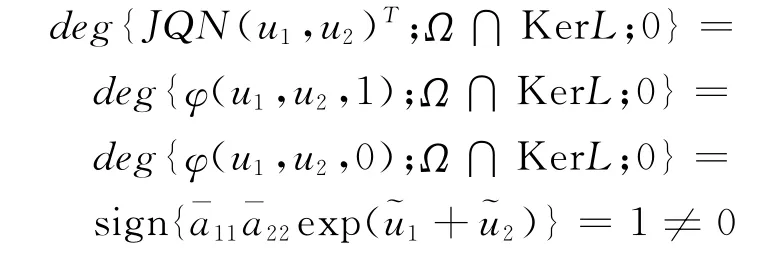
至此，引理1的條件全部滿足，于是系統（3）至少存在一個ω－周期解．

3 結束語

文獻［9] 也研究了具有時滯的Lotka－Volterra競爭模型的周期解問題，其使用的方法是中心流形方法和規范型理論．本文運用時標上連續拓撲度定理研究Lotka－Volterra競爭模型的周期行為，建立了這類系統的周期解存在的一個充分性判據，使此類系統的連續與離散情形的周期解問題得到統一．也就是說，如果系統（3）至少存在一個ω－周期解，則系統（2）和（4）至少存在一個ω－周期解．所得結果是對該類模型研究結果很好的補充．

［1] Ding W，Han M．Dynamic of a non－autonomous predator－prey system with infinite delay and diffusion［J] ．Comput Math Appl，2008，56（5）：1 335－1 350．

［2] Zhang Z，Hou Z，Li W．Multiplicity of positive periodic solutions to a generalized delayed predator－prey system with stocking［J] ．Nonlinear Anal，2008，68（9）：2 608－2 622．

［3] Sun Y G，Saker S H．Positive periodic solutions of discret three－level food－chain model of Holling type II［J] ．Appl Math Compu．，2006，180（1）：353－365．

［4] Fan M．Wang Q．Periodic solutions of a class of nonautonomous discrete time semi－ratio－dependent predator－prey systems［J] ．Discrete Contin Dyn Syst Ser B，2004，4（3）：563－574．

［5] Bohner M，Fan M，Zhang J M．Existence of periodic solutions in predator－prey and competition dynamic systems［J] ．Nonlinear Anal：RWA，2006，7（5）：1 193－1 204．

［6] 黃燕革，姚曉潔，黃勇．時間測度上具有Beddington－DeAngelis類功能反應和擴散的捕食系統的周期解［J] ．華南師范大學學報：自然科學版，2010，4（4）：19－26．

［7] 黎勇，秦發金．時間測度上具有Holling－N類功能反應和擴散的捕食系統的周期解［J] ．數學的實踐與認識，2010，40（2）：126－134．

［8] 劉振杰．時間測度上具有時滯基于比率的捕食者－食餌擴散系統的周期解［J] ．數學的實踐與認識，2008，38（24）：235－239．

［9] Zhang J，Jin Z，Yan J，et al．Stability and Hopf bifurcation in a delayed competition system［J] ．Nonlinear Anall，2009，70：658－670．

［10] Gaines R E，Mawhin J L．Coincidence degree and nonlinear differential equations［M] ．Berlin Springer－Verlag：1977．

［11] Fan M，Wang K．Periodic solutions of a discrete time nonautonomous ratio－dependent predator－prey system［J] ．Math Comput Modelling，2002，35（9－10）：951－961．