隨機信息中正態均值的灰色統計假設檢驗判定

李 勇

（重慶工商大學 數學與統計學院，重慶 400067）

1 灰數的定義

灰色系統理論是1982年由鄧聚龍教授原創的，是處理少數據不確定性問題的理論。少數據不確定性即稱灰性。而灰統計是指將統計對象的實際樣本通過白化權函數抽象為數字量（即灰統計量），按此灰統計量統計出對象所屬灰類的權。

灰數指只知道大概范圍而不知其確切值的數，常指某個區間或某個一般數集內取值的不確定數。本文的灰數主要指區間灰數?∈[a,b]，灰數的白化值記為?=ax+(1-x)b,x∈[0,1]，其白化權函數主要指三角形（態）（適中測度）白化權函數，其一般形式為

灰數的α截集[]α為

2 灰色統計檢驗統計量

假設X～(μ,σ2),σ2為已知。隨機抽取一組樣本量為n樣本，樣本均值為。設統計假設檢驗為

原假設:H0:μ=μ0? 對立假設:H1:μ≠μ0

其中灰數的α截集[α]為

3 灰色統計假設檢驗的檢驗判斷準則

設灰色檢驗統計量的兩個臨界值分別是灰數和，其白化值分別對應于和其中表示正態分布N(0,1)中滿足概率設此兩個臨界值灰數的α截集分別為和

首先，計算cv21(α)和cv22(α)，定義cv22(α)滿足下式

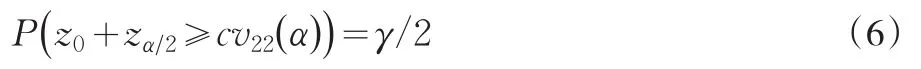
其中z0服從正態分布N(0 ,1)，有得：

同理，定義cv21(α)為

得：

其中，γ為定值且，0.01≤α≤1。

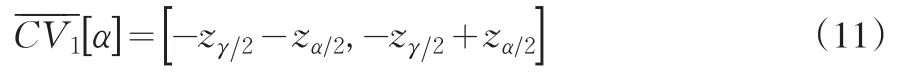
現在已經求得灰色檢驗統計量和臨界值灰色統計檢驗的決斷方法，是將依和的關系來決定，當Zˉ與比較時，將會得到三種結果：＜,＞,≈。其結果之九種組合情況見下表。

Zˉ 和 ------CV2比較CV2 Zˉ≈ ------CV2 Zˉ ＞ ------Zˉ 和------CV1比CV2 Zˉ＜ ------Zˉ ＜ ------CV1× 拒絕H0 ×較Zˉ ＞ ------CV1 Zˉ ≈ ------CV1拒絕H0 接受H0 無法判斷× 無法判斷 無法判斷

（1）灰色統計決斷為“拒絕H0”的組合有兩個：且且

（2）灰色統計決斷為“接受H0”的組合有一個：Z且

根據上述規則，可以進行灰色統計檢驗的判斷（拒絕H0、接受H0或無法判斷）。

4 灰色統計假設檢驗判定

灰色檢驗統計量Zˉ和臨界值的白化權函數都是三角形（態）（適中測度），且根據和臨界值的α截集，可知灰色統計量Zˉ和臨界值的白化值分別為和利用關于灰數排序的方法，對Zˉ 和臨界值比較。

首先，對灰色檢驗統計量和右尾臨界值比較，比較兩個灰數的白化值大小，其結果說明如下：

同理，對灰色檢驗統計量和左尾臨界值比較，以類似方法來判斷。故其灰色統計決斷方法歸納如下：

5 實例應用

例：設X～N(μ,σ2)，μ0=1,σ=2。現根據簡單隨機抽樣獲得一組來自該總體的有效隨機樣本X1,...,X100，其樣本均值為=1.32。在檢驗水平γ=0.05下，進行灰色統計檢驗（其中0.01≤α＜1）。

解：因為檢驗水平γ=0.05，得又

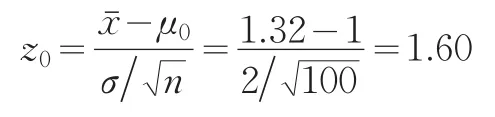
根據判斷準則得，灰色統計檢驗結果是：無法判斷。需要進一步的檢驗才能確定。

6 結論

利用隨機信息進行參數的假設檢驗，是數理統計學的基本內容。但經典統計學的方法，都是建立在明確數據上的參數假設檢驗。而現實中的大多數據，帶有模糊或灰色數據。本文借助于灰色系統的方法，建立了在隨機樣本的信息下，正態均值的灰色統計假設檢驗方法。并列舉實例與經典的N-P假設檢驗方法進行比較，從而說明灰色統計假設檢驗方法能夠提供更多的有效信息。

[1] 劉思峰，黨耀國，方志耕等.灰色系統理論及其應用（5版）[M].北京：科學出版社，2010.

[2] 李勇，張維，陳正偉.隨機樣本中正態均值的灰色區間估計研究[J].統計與決策，2010,（13）.

[3] Li Yong.The Study on the Gray Interval Estimation of Normal Means in Variance Unknown[C].2010 International Institute of Statistics&Management Engineering Symposium，2010,08.

[4] James J.Buckley，Fuzzy Statistics[M].Berlin：Springer-Verlag,2004.