隨機(jī)系數(shù)SETAR模型的應(yīng)用

莫達(dá)隆,宋立新

（1.賀州學(xué)院，廣西 賀州542800；2.大連理工大學(xué)，遼寧大連 116024）

0 引言

門限自回歸模型TAR是Tong.H于1978年提出來(lái)的,此后Tong和Lim(1980年)又給出了自激發(fā)門限自回歸模型SETAR。由于SETAR模型能根據(jù)自變量的變化，選擇不同的線性模型，這種選擇轉(zhuǎn)換被稱之為機(jī)制轉(zhuǎn)換。正是這種機(jī)制轉(zhuǎn)換特征恰好描述了現(xiàn)實(shí)生活的大量現(xiàn)象,如經(jīng)濟(jì)、金融、氣候等領(lǐng)域的現(xiàn)象,這些領(lǐng)域的數(shù)據(jù)受多種因素影響，觀測(cè)值序列呈現(xiàn)跳躍性的變化，使得SETAR模型在這些領(lǐng)域的數(shù)據(jù)分析中得到廣泛應(yīng)用。

正如SETAR模型應(yīng)用者的研究發(fā)現(xiàn),SETAR模型是利用門限空間來(lái)改進(jìn)線性逼近,現(xiàn)實(shí)生活的各種系統(tǒng)卻充滿著時(shí)變性,要提高預(yù)測(cè)的準(zhǔn)確性,預(yù)測(cè)系統(tǒng)模型的回歸系數(shù)也應(yīng)該時(shí)常得到更新。本文提出隨機(jī)系數(shù)SETAR模型及其應(yīng)用，并假設(shè)其回歸系數(shù)是一個(gè)隨機(jī)時(shí)間變化的隨機(jī)系數(shù)，給出了回歸系數(shù)的估計(jì)方法.實(shí)證研究證明,所建立的模型能更準(zhǔn)確地?cái)M合現(xiàn)實(shí)數(shù)據(jù)序列,為拓展SETAR模型的應(yīng)用提供了一種新的方法。

1 隨機(jī)系數(shù)SETAR模型

設(shè)

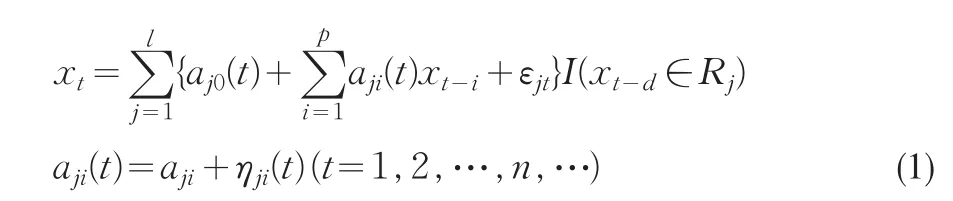
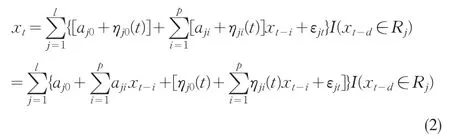
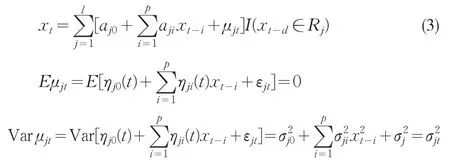
把(3)式寫成向量形式:

其中,Y是觀測(cè)值xt,t=p+1,p+2,…,n,

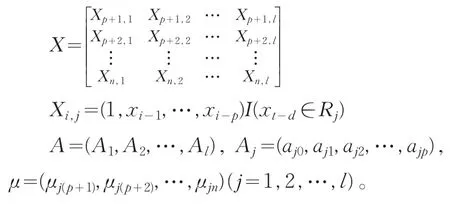
1.1 模型識(shí)別和估計(jì)

設(shè)xt,t=1,…,n是依時(shí)間順序排列的n個(gè)觀測(cè)值，現(xiàn)要估計(jì)參數(shù)A,d，確定階數(shù)p和分割{ }Rj.具體步驟如下：

步驟一，假設(shè)階數(shù)p和分割{ }Rj已知.根據(jù)觀測(cè)值xt,t=1,…,n給出A的條件最小二乘估計(jì)（CLSE），即極小化如下的殘差平方和：

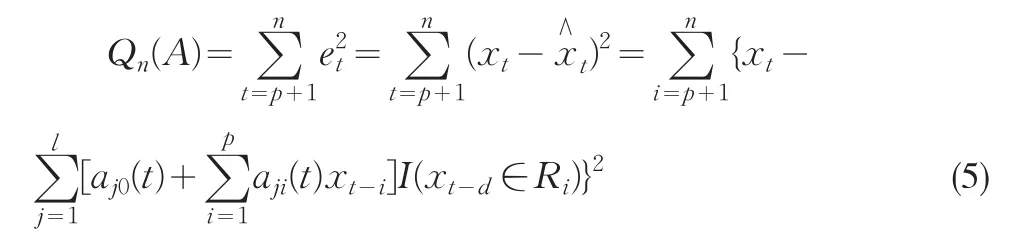
記A的CLSE值為，則

但由(3)式可知，模型(4)是一個(gè)異方差模型，宜用加權(quán)最小二乘法對(duì)模型(4)的系數(shù)A進(jìn)行估計(jì)，加權(quán)最小二乘估計(jì)為

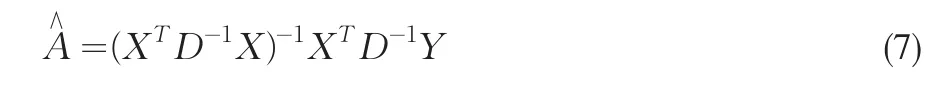
其中,D=diag(dp+1,dp+2,…,dn)是權(quán)矩陣

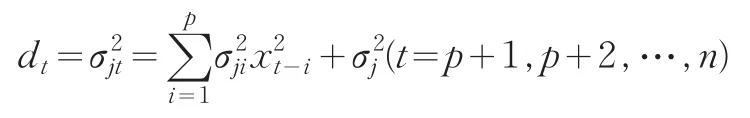
具體計(jì)算權(quán)矩陣D時(shí)，可用模型（4）的CLSE估計(jì)的殘差估計(jì)量作為對(duì)角線元素來(lái)構(gòu)造權(quán)矩陣D的初步估計(jì)。dt是隨時(shí)間變化的，經(jīng)過(guò)權(quán)矩陣D的作用有可能尚未把異方差的因素去掉，可重復(fù)地對(duì)模型(4)進(jìn)行加權(quán)最小二乘法估計(jì),迭代到模型的殘差平方和穩(wěn)定為止。

步驟二，估計(jì)Ri.固定d，關(guān)于R極小化，可先根據(jù)數(shù)據(jù)序列直觀分析，預(yù)先確定一些門限候選值，在這些值處比較最優(yōu)殘差平方和Qn(A)的大小，取使得Qn(A)最小的候選值作為。例如,先將數(shù)據(jù)序列從小到大重新排列，以位于數(shù)據(jù)量0.25，0.35，0.45，0.55，0.65和0.75分位數(shù)處的xt的取值作為門限候選值。

步驟三,關(guān)于d極小化,估計(jì)d.對(duì)每個(gè)固定d，先對(duì)j=1,2,…,l，極小化（4）式，然后選擇使得（5）式達(dá)到最小。

1.2 隨機(jī)系數(shù)SETAR的統(tǒng)計(jì)檢驗(yàn)

隨機(jī)系數(shù)SETAR的統(tǒng)計(jì)檢驗(yàn)包括三個(gè)方面:

(1)殘差的常規(guī)檢驗(yàn).如殘差的獨(dú)立性、正態(tài)性和等方差性檢驗(yàn)。

(2)非線性檢驗(yàn)。這里應(yīng)用廣義似然比檢驗(yàn)方法,該方法假設(shè)檢驗(yàn)問(wèn)題是：

H0:a1i=a2i=…=ali,i=0,1,2,...,p

H1:a1i,a2i,…ali,.i=0,1,2,…,p不全相等。

構(gòu)造其統(tǒng)計(jì)量為：

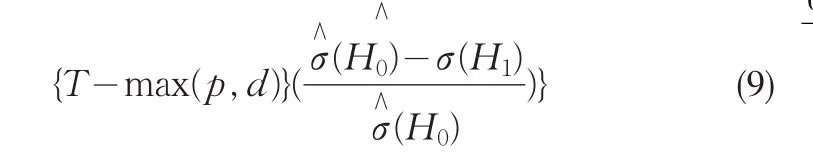
2 實(shí)例分析

2.1 數(shù)據(jù)獲取和初步分析

取廣西外經(jīng)貿(mào)2005年1月－2010年4月的出口數(shù)據(jù)為例分析之(見表1，數(shù)據(jù)來(lái)源：廣西商務(wù)之窗http://guangxi.mofcom.gov.cn/.統(tǒng)計(jì)數(shù)據(jù)中的進(jìn)出口數(shù)據(jù)，單位：萬(wàn)美元)。其中,取2005年1月～2009年12月的出口數(shù)據(jù)作為分析數(shù)據(jù),2010年1月～4月為預(yù)測(cè)用的數(shù)據(jù)。（所用統(tǒng)計(jì)軟件為eviws和R語(yǔ)言，自行編程）

為初步觀察數(shù)據(jù)的平穩(wěn)性，作廣西累計(jì)出口月金額數(shù)據(jù)序列圖和相關(guān)函數(shù)圖。由此可以判斷：廣西累計(jì)出口月金額數(shù)據(jù)序列有明顯長(zhǎng)期趨勢(shì)，因是月度數(shù)據(jù)，很有可能存在季節(jié)趨勢(shì)。可計(jì)算其季節(jié)指數(shù)，若存在季節(jié)趨勢(shì)可先剔除季節(jié)趨勢(shì)，再通過(guò)單位根（ADF）檢驗(yàn)其平穩(wěn)性，并確定長(zhǎng)期趨勢(shì)是確定性趨勢(shì)還是隨機(jī)性趨勢(shì)，從而選擇適當(dāng)方法剔除長(zhǎng)期趨勢(shì)即可得到一平穩(wěn)序列。

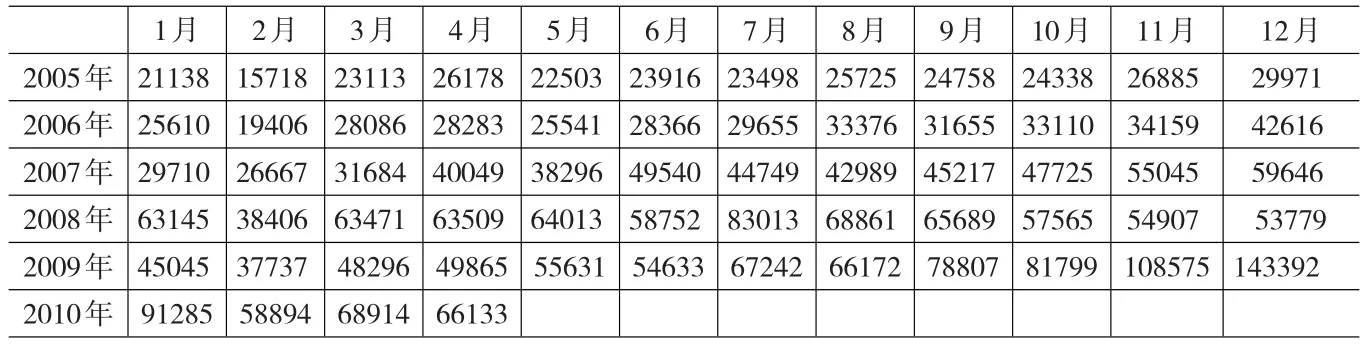
表1

剔除季節(jié)趨勢(shì)的方法有季節(jié)差分、計(jì)算季節(jié)指數(shù)再消除季節(jié)因素等方法，因?yàn)樵撛夹蛄械娜萘枯^少(n=64)，如果用季節(jié)差分消除季節(jié)因素，勢(shì)必會(huì)缺失相當(dāng)多的數(shù)據(jù)。所以通過(guò)計(jì)算季節(jié)指數(shù)消除季節(jié)因素的方法剔除季節(jié)變動(dòng)。用移動(dòng)平均法，得廣西累計(jì)出口月金額數(shù)據(jù)的季節(jié)指數(shù)表(見表2)：

根據(jù)季節(jié)指數(shù)發(fā)現(xiàn)，原序列有季節(jié)趨勢(shì)，在上半年和下半年稍有變化.可剔除季節(jié)趨勢(shì)，設(shè)剔除原序列中的季節(jié)因素后的序列為{Zt}。

2.2 對(duì)序列{Zt}進(jìn)行ADF檢驗(yàn)，確定序列均勢(shì)類型

經(jīng)嘗試，有如下結(jié)果：（見圖1，見圖2）

圖1、圖2顯示：檢驗(yàn)t統(tǒng)計(jì)量值是-0.491272,大于顯著水平為5%和10%的臨界值，同時(shí)時(shí)間項(xiàng)T的t統(tǒng)計(jì)量小于臨界值，可斷定序列{Zt}存在單位根，是具有隨機(jī)性趨勢(shì)的時(shí)間序列，對(duì)其零均值化，得到的新序列設(shè)為{Yt}。因序列{Yt}是具有隨機(jī)性趨勢(shì)的時(shí)間序列，要通過(guò)差分的方法來(lái)消除隨機(jī)性趨勢(shì)。

表2

圖1

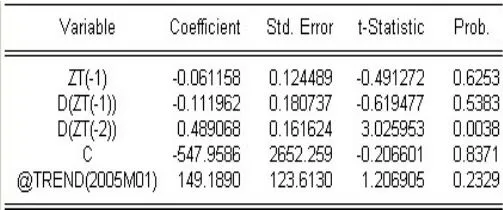
圖2

經(jīng)嘗試，對(duì){Yt}兩階差分（仍設(shè)為序列{Yt}）后進(jìn)行ADF檢驗(yàn)，檢驗(yàn)t統(tǒng)計(jì)量值是-8.906645,小于顯著水平為5%和10%的臨界值，時(shí)間項(xiàng)T的t統(tǒng)計(jì)量也小于臨界值，表明序列{Yt}是平穩(wěn)的，滯后項(xiàng)m=2，可初步估計(jì)序列{Yt}有滯后項(xiàng)為3的自回歸模型。

2.3 利用ARMA(q,p)模型建模

利用Pandit-Wu建模方法對(duì)序列{Yt}擬合AR(1)、ARMA(3,1)、ARMA(5,3)、ARMA(4,3)、ARMA(2,1)等模型進(jìn)行對(duì)比選擇。

擬合相關(guān)結(jié)果如下（見表3）：

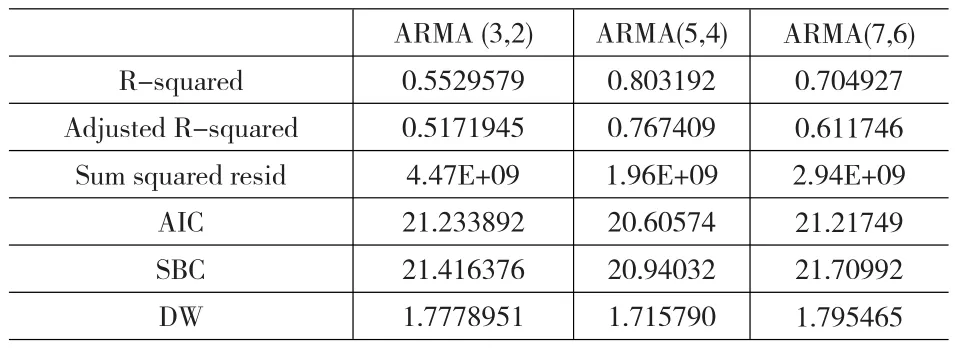
表3

綜合表3的各項(xiàng)因素，ARMA(5,4)是一個(gè)最佳的模型，模型形式如下：

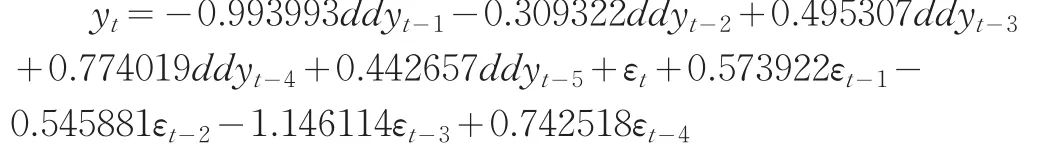
2.4 利用隨機(jī)系數(shù)SETAR模型建模

根據(jù)上文的單位根檢驗(yàn)可初步確定階數(shù)為p=3,序列有季節(jié)趨勢(shì)且在上半年和下半年稍有變化，可暫取第18個(gè)序列數(shù)據(jù)Y18=-78作為門限值r，d=2(1≤d≤p),由式(6)得到系數(shù)A的初步估計(jì)

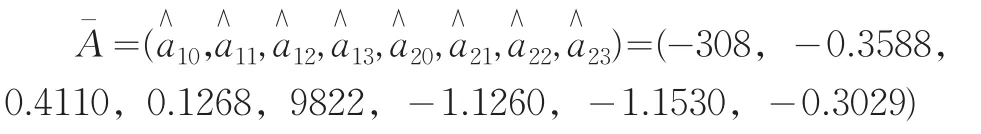
現(xiàn)要進(jìn)行異方差檢驗(yàn)，作模型的殘差圖和標(biāo)準(zhǔn)殘差圖，從這兩個(gè)殘差圖可明顯看出殘差呈異方差分布，可利用加權(quán)最小二乘法估計(jì)模型(4)的系數(shù)A。先抽取模型(4)的殘差估計(jì)量，定義權(quán)矩陣D為再由式(6)得系數(shù)A的加權(quán)最小二乘估計(jì)D-1Y。經(jīng)迭代，A最佳的結(jié)果是：

先固定d=2，因數(shù)據(jù)序列是月度數(shù)據(jù)，且根據(jù)3.1節(jié)分析發(fā)現(xiàn)數(shù)據(jù)有兩個(gè)季度的季節(jié)趨勢(shì)，便取第18、24、36、42個(gè)數(shù)據(jù)作為門限候選值，分別極小化(5)式，發(fā)現(xiàn)當(dāng)r=2872時(shí)，式(5)最小，故暫取r=2872.固定r=2872，分別對(duì)d=1、2、3時(shí)極小化式(5)，發(fā)現(xiàn)當(dāng)d=2時(shí)，式(5)最小，故取d=2。上述過(guò)程用表4來(lái)表示：

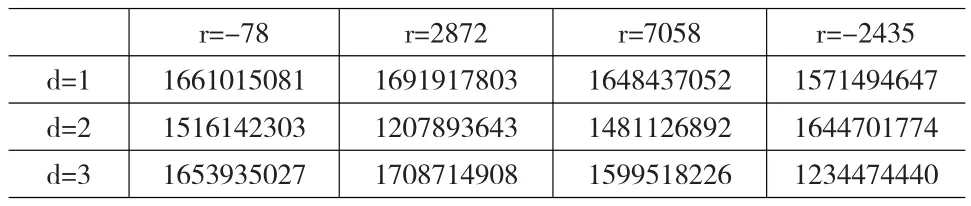
表4

從表4中可看出，r=2872,d=2時(shí)殘差平方和最小。因此可建立如下模型

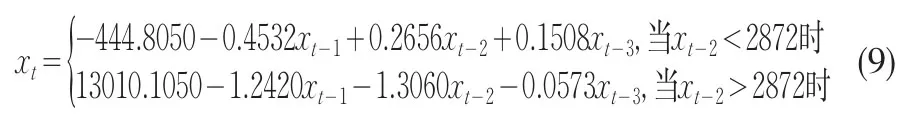
2.5 對(duì)模型(9)的統(tǒng)計(jì)檢驗(yàn)

首先,做殘差的常規(guī)檢驗(yàn).模型解決了異方差問(wèn)題，現(xiàn)對(duì)殘差的獨(dú)立性和正態(tài)性進(jìn)行檢驗(yàn)，結(jié)果有：W=0.9776,P-Value=0.4043。滿足正態(tài)性檢驗(yàn)。

然后，進(jìn)行非線性檢驗(yàn).采用廣義似然比檢驗(yàn)，有如下結(jié)果：

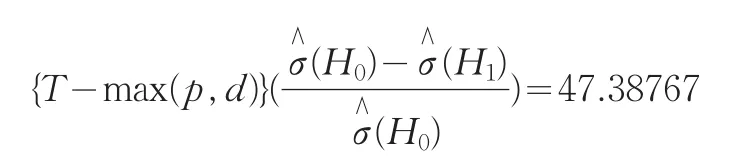
該值遠(yuǎn)遠(yuǎn)大于水平0.1%的臨界值27.20[4],拒絕H0假設(shè),即線性模型的假設(shè)不成立.

最后,對(duì)系數(shù)進(jìn)行顯著性檢驗(yàn)。

R語(yǔ)言編程計(jì)算結(jié)果如下：

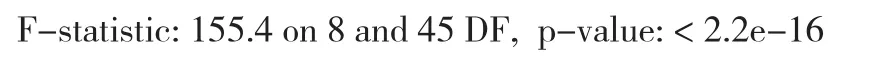
上述結(jié)果表明，除了當(dāng)r＞2872時(shí)，xt-3的系數(shù)不顯著外，其他系數(shù)的P值均小于0.05，所以應(yīng)該是非常顯著的。相關(guān)系數(shù)的平方為0.9651，關(guān)于F分布的P值也大大小于0.05，也非常顯著。因此可以認(rèn)為模型通過(guò)了檢驗(yàn)。

2.6 預(yù)測(cè)

用ARMA(5,4)模型和隨機(jī)系數(shù)SETAR模型預(yù)測(cè)2010年第一季度的廣西出口金額數(shù)據(jù)的對(duì)比，如下表：

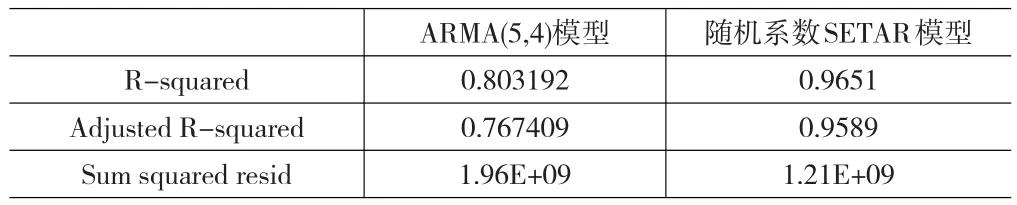
表6

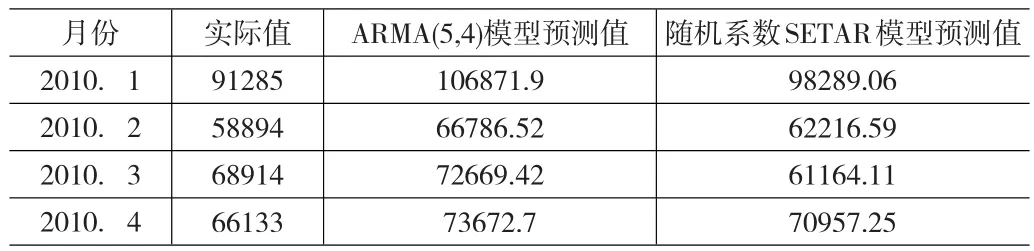
表7

從表6、表7可看出：隨機(jī)系數(shù)SETAR模型無(wú)論是擬合程度還是預(yù)測(cè)結(jié)果都要比ARMA(5,4)模型好。

3 結(jié)論

本文提出了隨機(jī)系數(shù)SETAR模型回歸系數(shù)估計(jì)的方法，并利用隨機(jī)系數(shù)SETAR模型對(duì)一個(gè)月度數(shù)據(jù)進(jìn)行建模，拓展了SETAR模型的應(yīng)用范疇，同時(shí)還建立了ARMA模型進(jìn)行比較研究.結(jié)果證明隨機(jī)系數(shù)SETAR模型在具有非線性性質(zhì)的數(shù)據(jù)序列建模中有較大優(yōu)勢(shì)。

[1] 范劍青,姚琦偉.陳敏譯.非線性時(shí)間序列-建模、預(yù)報(bào)及應(yīng)用[M].北京：高等教育出版社,2005.

[2] 安鴻志,陳敏.非線性時(shí)間序列[M].上海：上海科學(xué)技術(shù)出版社,1998.

[3] 袁軍.SETAR模型在GDP預(yù)測(cè)中的應(yīng)用[J].統(tǒng)計(jì)與決策,2007,(5).

[4] 王黎明等.應(yīng)用時(shí)間序列分析[M].上海：復(fù)旦大學(xué)出版社,2009.

[5] 王振龍等.應(yīng)用時(shí)間序列分析[M].北京：科學(xué)出版社,2007.

[6] 趙松山.關(guān)于時(shí)變參數(shù)建模的研究[J].東北財(cái)經(jīng)大學(xué)學(xué)報(bào),2002,(9).

[7] 李書進(jìn)，李文華.基于自適應(yīng)卡爾曼濾波的時(shí)變結(jié)構(gòu)參數(shù)估計(jì)[J].廣西大學(xué)學(xué)報(bào)(自然科學(xué)版),2004,(6).

[8] 胡琨.基于時(shí)變參數(shù)模型的創(chuàng)新環(huán)境影響研究[J].科技管理研究，2010,(1).

[9] 王宏禹,邱天爽.線性離散系統(tǒng)[M].北京:國(guó)防工業(yè)出版社,2008.

[10] 韓志剛.多層進(jìn)階方法及其應(yīng)用[M].北京:科學(xué)出版社,1989.