高層建筑抗震計算數值方法分析

周清橋

0 引言

結構的抗震計算分析方法有很多，本文根據高層建筑結構的特點，對其進行抗震計算分析。

1 計算模型

多層結構往往采用層剪切模型來計算。而像更高層數的結構，其結構往往是筒體或框架剪力墻結構，則適合采用彎剪層模型。而桿模型以梁、柱等單根構件為基礎單元，將樓層質量分別集中于結構各節點，形成質點。桿模型是較為精確的計算模型，我們采用的計算模型是層剪切模型，其方程如下［1］:

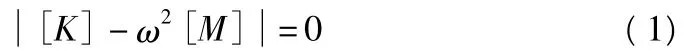
2 數值計算方法

2． 1 結構非線性計算方法

式(1)是非線性方程，需要用數值方法求解。但這里我們采用比較有代表性的Newton-Raphson法，在進行非線性求解時具體采用增量Newton-Raphson方法，此方法是先把荷載分成若干增量(或荷載步)，然后在每個增量步內用Newton-Raphson方法進行迭代求解。

圖1是增量Newton-Raphson方法求解非線性方程F=Kδ的圖解。圖1中荷載 F 分成了 i個增量步(F1，F2，…，Fi-1，Fi)，現以第一增量步為例說明Newton-Raphson方法的迭代過程。在直角坐標系F—δ中，第一增量步內直線F1=R和曲線F=Kδ的交點A的橫坐標δA就是方程F=Kδ在第一增量步內的解。

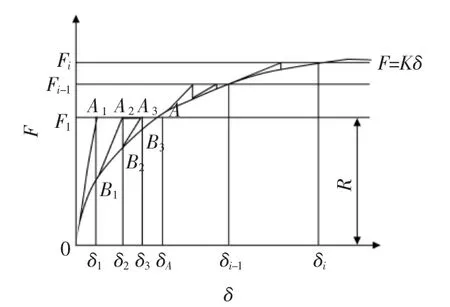
圖1 增量Newton-Raphson方法

在實際使用中，Newton-Raphson法開始需先按線性理論求出位移δ1作為第一次迭代近似值，即圖1中A1點的橫坐標，如果荷載R并不因變形而改變它的數值和方向(假設為小變形)，則得［2］:

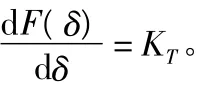
其中，KT為曲線F=Kδ的斜率(或切線剛度)。

第二次迭代從B1點做曲線F=Kδ的切線交直線F1=R于A2點，取A2點的橫坐標δ2，從圖1中可見:

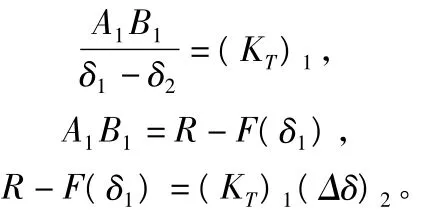
由圖1看出δ2就是位移的第二次迭代近似值。如此重復可得以下迭代公式:

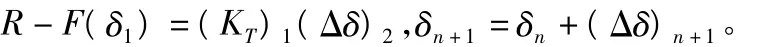
不斷重復迭代直至滿足收斂條件為止，便可得到最終結果。……