基于相空間的滾動軸承振動特征參數的乏信息分析

高磊磊，夏新濤，樊雎，孫小超

(河南科技大學 機電工程學院，河南 洛陽 471003)

滾動軸承的振動水平是軸承動態性能質量的重要反映[1]，因此一直受到相關工程與學術界的重視。文獻[2-3]基于軸承振動信號數據分別用時域特征和神經網絡法進行軸承故障的診斷處理。文獻[4]對軸承振動信號數據進行光譜分析等處理并用于軸承的故障診斷。文獻[5]用灰自助法對軸承振動數據進行了動態評估與診斷。文獻[6]提出了基于Hilbert-Huang變換的軸承振動特性分析的新方法。現有的研究大多尚未關注乏信息系統領域。乏信息是指研究對象所表現出的屬性特征信息不完整與不充分。乏信息系統的參數估計，目前是信息科學與系統科學領域的前沿與熱點之一，具有重要的理論意義和實用價值。

乏信息系統的相空間重構理論是分析研究非線性動力系統的基礎，相空間是描述系統演化與運動最有力的工具。用混沌理論進行相空間重構，能使軸承振動時間序列的原始動力學特征得到最優恢復。

研究表明，軸承振動具有不確定的明顯波動和趨勢變化，屬于概率分布和趨勢規律都未知的乏信息系統。下文基于乏信息相空間，用最大熵自助法[7-8]分別建立當前樣本和先驗樣本的概率密度函數，然后結合Bayes統計理論，建立軸承振動特征參數的動態Bayes后驗概率密度函數，最后對特征參數進行點估計、區間估計及趨勢估計等，從而為軸承性能的非線性動力學特征演變評估奠定新的理論基礎。

1 乏信息數學模型

針對軸承振動特征參數的評估，用乏信息系統理論進行相空間重構，并結合最大熵自助法和Bayes統計理論構建數學模型進行參數估計。

1.1 相空間重構

設軸承振動信號的時間序列為

X=(x(1),x(2),…,x(k),…,x(N));k=1,2,…,N；

(1)

式中：x(k)為第k個數據；N為時間序列X中數據的個數。

重構相空間[9]，得到一組新的向量序列

X(t)=(x(t),x(t+τ),…,x(t+(k-1)τ),…,x(t+(m-1)τ))；t=1,2,…,M;k=1,2,…,m;

(2)

M=N-(m-1)τ；

(3)

式中：x(t)為t時刻的觀測值；x(t+(m-1)τ)為延遲值；m為嵌入維數；τ為延遲時間；M為相點個數。

(1)式是由觀測值x(t)和延遲值x(t+(m-1)τ)所構成的m維乏信息相空間，其與原始的狀態空間微分同構。

至此，乏信息過程的原始動力學特征得到最優恢復。選定當前時刻t，將此刻的相軌跡作為中心軌跡。從當前時刻t往前隔(τ-1)個數據取一個，得到一個含有m個數據的樣本X1，即為基于中心軌跡的當前樣本。先驗樣本就是當前時刻t以前的歷史軌跡，從時刻(t-1)往前隔(τ-1)個數據取一個，得到一個含有m個數據的樣本。讓t依次往前滾動遞減，重復以上步驟，即可得到多個含有m個數據的樣本序列Xi。

借鑒混沌預測的思想，從樣本序列Xi中找出與當前樣本X1最相似的樣本X2，即為基于歷史軌跡的先驗樣本。因為樣本序列Xi中很多樣本信息對于當前時刻的參數估計已經沒有太大價值，應予以剔除。用2-范數法來確定Xi與X1的相似度，

(4)

式中：xij為Xi的第j個元素；x1j為X1的第j個元素。

通過計算，找出(4)式值最小的樣本，即為先驗樣本X2。

由于樣本X1和X2中數據較少，還須用自助法抽樣，以便建立基于當前樣本和先驗樣本的最大熵概率密度函數。

1.2 自助樣本

從X中等概率可放回地抽樣，抽取m個數據，得到一個樣本Xb，共抽取B次，得到B個自助樣本，

Xb=(xb(1),xb(2),…,xb(k),…,xb(m));b=1,2,…,B；

(5)

式中：Xb為第b個自助樣本；xb(k)為第b個自助樣本的第k個數據，k=1,2,…,m。

求自助樣本Xb的均值為

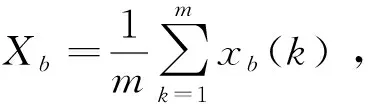
(6)

從而得到一個樣本含量為B的自助樣本

XBootstrap=(X1,X2,…,Xb,…,XB)。

(7)

用自助法[10]分別對當前樣本X1和先驗樣本X2進行抽樣處理，得到當前自助樣本X1Bootstrap和先驗自助樣本X2Bootstrap。

1.3 最大熵概率密度函數

根據最大熵原理，最無主觀偏見的概率密度函數應滿足熵最大，即

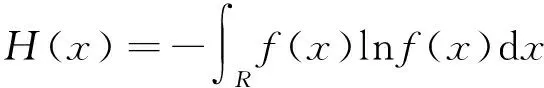
(8)

式中：R為積分空間。約束條件為各階原點距，

(9)

式中：k為原點距數；wk為第k階原點距；w為所用到的最高價原點距的階次，一般w=3～8，常用w=5。

在約束條件下調節f(x)可使熵最大，這是約束優化問題，用Lagrange乘子法可求出f(x)的表達式，

(10)

式中：ck為第k個Lagrange乘子，k=1,2,…,w。第1個Lagrange乘子c0為

(11)

其他w個乘子滿足

(12)

將上式用向量表示為

G=G(c)=(gk;k=1,2,…,w)T=0,

(13)

且有

c=(ck;k=1,2,…,w)T，

(14)

式中：c為Lagrange乘子列向量。可用Newton法求解Lagrange乘子向量c，即有

cj+1=cj-G′(cj)-1G(cj) (j=0,1,…) ，

(15)

式中：G′(cj)為迭代到第j步的Jacobi矩陣。迭代收斂的范數準則為

‖Gj+1-Gj‖1≤ε，

(16)

式中：ε為收斂誤差，一般取ε=10-12。

上述求解中，第k階原點距由前面得到的自助樣本XBootstrap確定。

用最大熵法分別對當前自助樣本X1Bootstrap和先驗自助樣本X2Bootstrap進行處理，得到當前樣本的最大熵概率密度函數f1(x)和先驗樣本的最大熵概率密度函數f2(x)。最后再結合Bayes統計理論，得到基于相空間的軸承振動特征參數的Bayes后驗概率密度函數。

1.4 Bayes概率密度函數

Bayes統計[11]認為，任何一個未知量θ都可以看成隨機變量，應用一個概率分布去描述對θ的未知狀況。這個概率分布是在抽樣前就有的關于θ的先驗信息的概率陳述，其稱為先驗分布。為了在小子樣下獲得好的參數估計，就必須利用參數的歷史資料即先驗信息。Bayes統計認為，后驗分布綜合了先驗和樣本的信息，可對參數做出較先驗分布更合理的估計。

Bayes公式的概率密度函數形式為

(17)

式中：θ為統計推斷參數；Θ為參數空間，Θ={θ}；x為總體分布產生的一個樣本，x=(x1,x2,…,xn)；f(θ|x)為在樣本x給定下θ的條件分布，即后驗分布；h(x|θ)為總體指標X的條件分布；f(θ)為先驗分布。

根據當前樣本的概率密度函數f1(x)和先驗樣本的概率密度函數f2(x),再結合Bayes統計原理，得出Bayes后驗概率密度函數為

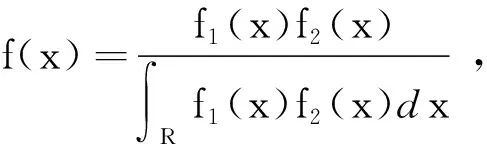
(18)

式中：x為樣本均值。

2 特征參數估計

基于Bayes概率密度函數進行參數估計。

估計真值X0為

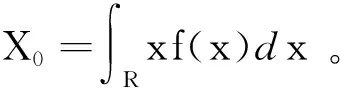
(19)

設顯著水平α∈[0,1]，估計區間的下邊界值XL應滿足

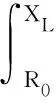
(20)

上邊界值Xu應滿足

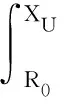
(21)

于是，在置信水平P=(1-α)×100%下，樣本均值的估計區間為[XL,XU]。

3 試驗研究與討論

采用美國Case Western Reserve University電氣工程實驗室的軸承故障模擬試驗臺的試驗數據進行研究分析。選取驅動端轉速為1 796 r/min，采樣頻率為12 kHz時得到的鋼球故障數據時間序列進行驗證，其中損傷直徑為0.1 778 mm。取數據文件里的前1 000個數據作為時間序列進行建模處理。

在計算最大熵概率密度函數時，取w=5,Q=9，ε=10-12，數據的時域信息及利用乏信息數學模型估計得到的結果如圖1和圖2所示。在計算特征參數時，取α=0.05，B=10 000，圖2中選定當前時刻t為1 000個振動數據的第732個，每計算一次讓t自動加1，連續計算10次，將估計結果繪制成圖像。

由圖1可知，在測量過程中，隨著軸承的轉動(原始數據序列號 從1增加到1000)，軸承振動的時域信息具有明顯的隨機波動和趨勢變化特征，可見軸承振動的時域信息很復雜。

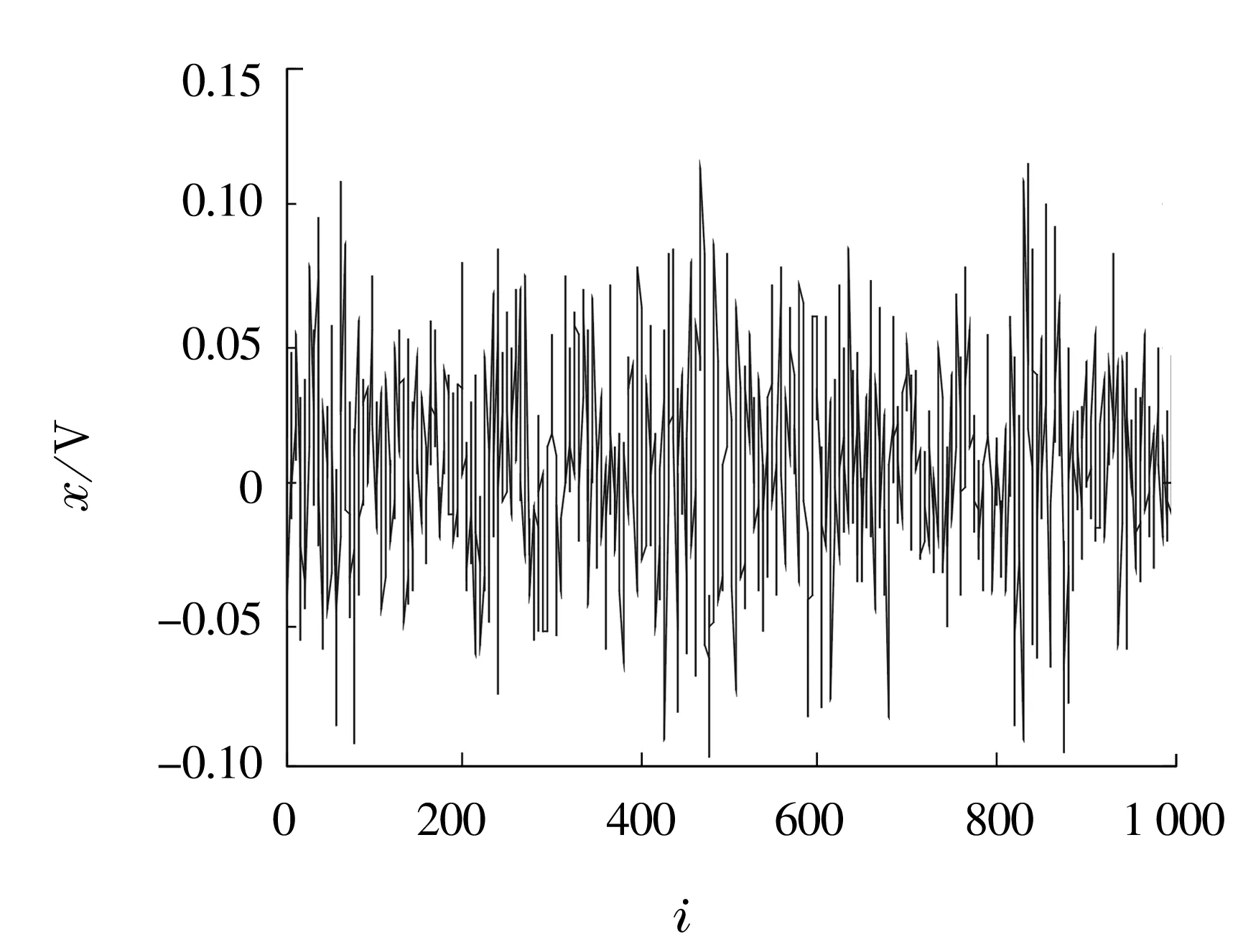
圖1 軸承振動數據

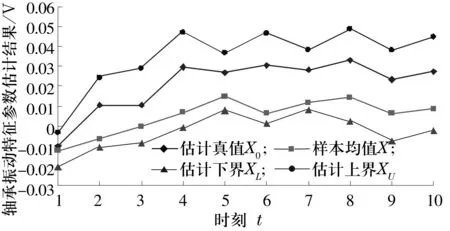
圖2 估計區間對樣本均值的包絡

由t=1～10各時刻的Bayes概率密度函數可知，從t=1～10，軸承振動的Bayes概率密度函數處于不斷變化之中，其中t=3時概率密度函數近似于正態分布，其余時刻概率密度函數呈現非對稱的單峰形或多峰形(圖3)，這是隨機過程短期的多次實現的結果，可見軸承振動的概率分布信息非常復雜且具有不確定性。這些復雜信息實際上隱含著系統真值的一些特征。

根據圖2所示，軸承振動數據的樣本均值序列X被完美地包絡在估計區間[XL，XU]之中，且估計真值X0與樣本均值X非常接近。可以看出，t=1時估計真值X0與樣本均值X之間的絕對誤差小到0.002 5；t=6時估計真值X0與樣本均值X之間的絕對誤差最大為0.024 0。這說明利用乏信息數學模型處理振動數據能得到比較合理的結果。因此，估計結果的誤差可以滿足工程要求。這也證實了所提出的數學模型是合理與可行的，基本上可以真實描述軸承振動的統計特征。

4 結論

相空間是描述系統演化與運動最有力的工具。用混沌理論進行相空間重構，使軸承振動時間序列的原始動力學特征得到最優恢復。在相空間里，建立了基于最大熵自助法和Bayes統計理論的軸承振動的動態Bayes后驗概率密度函數。軸承振動的Bayes概率密度函數呈非對稱的單峰形或多峰形，這是隨機過程短期的多次實現的結果。這刻畫了軸承振動不確定的明顯波動和趨勢變化特征。

以Bayes概率分布函數為基礎，提出了軸承振動特征參數的真值估計、區間估計和趨勢估計方法。從計算結果來看，軸承振動數據的樣本均值都能被估計區間完美地包絡，且估計結果和試驗結果在數值上很接近，滿足工程要求。從而為軸承性能的非線性動力學特征演變評估奠定新的理論基礎。

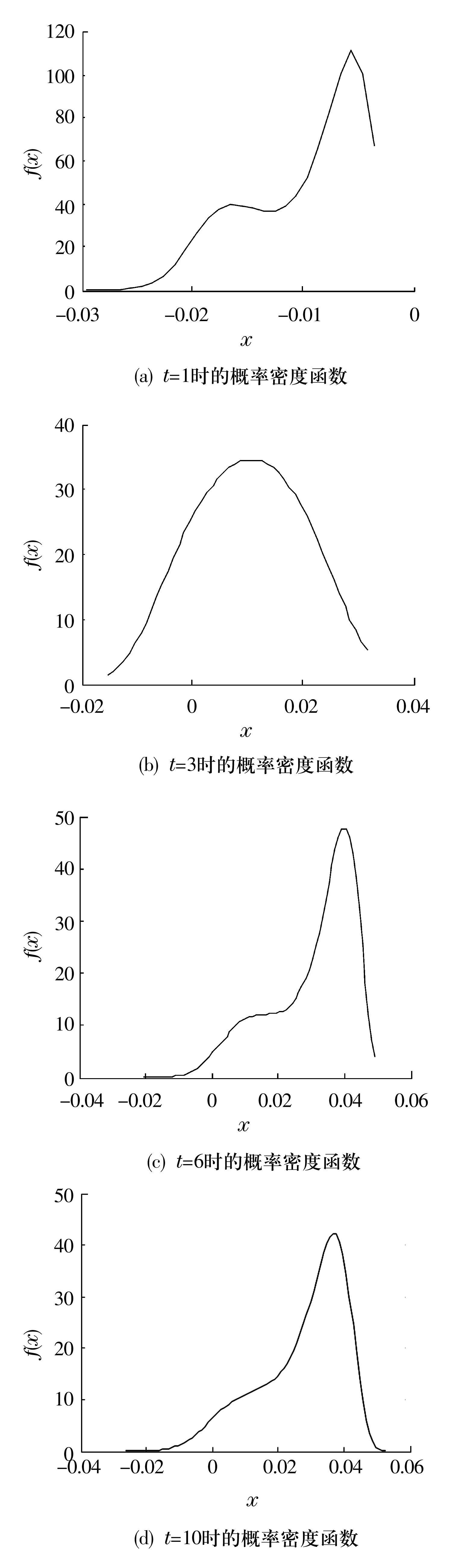
圖3 t=1,3,6,10時刻的概率密度函數