回歸分析在電機冷卻系統(tǒng)中的應用

李朝軍，牛偉光

(北京中電科電子裝備有限公司，北京 100176)

回歸分析是健壯設計方法與6 σ質(zhì)量管理有效分析工具。在工程技術領域，系統(tǒng)中若干變量之間存在著某種相互聯(lián)系、相互制約的依存關系，而這種關系并不是嚴格的函數(shù)關系，而是一種非確定性的關系。回歸分析就是研究系統(tǒng)中一個變量與其他若干變量之間的相關關系的數(shù)學工具，回歸分析建立在一組試驗、觀測資料的基礎上，用一種確定的函數(shù)關系來近似地代表比較復雜的相關關系。建立回歸函數(shù)，這個回歸函數(shù)就是工程中提及的經(jīng)驗公式。

全自動引線鍵合機主要包括：xy工作平臺、鍵合頭、物料夾持臺、上下料裝置等部件。鍵合機在工作過程中，由Z向電機驅(qū)動的鍵合頭，配合精密xy運動平臺，引導金屬線在三維空間作復雜高速的運動，以便形成各種滿足不同芯片封裝所需的線弧。xy平臺是全自動引線鍵合機的關鍵部件，為了提高機臺的UPH與穩(wěn)定性，xy平臺的性能以及穩(wěn)定性對于整個機器至關重要，本論文目的是建立xy平臺中y向驅(qū)動電機冷卻系統(tǒng)中電機工作時間與冷卻后線圈溫度之間的關系，建立經(jīng)驗公式，以便對線圈溫度進行預測與監(jiān)控。

1 回歸分析的數(shù)學模型

為了回歸函數(shù)的擬合效果，盡量使用高的階次，但是實際工程中，最多使用4次階，更高的階次雖然能取得更好的擬合效果，但是估計與預測值的方差會變大，在此文中，采用3次多項式的數(shù)學模型，3階數(shù)學模型能夠描述變量的‘峰谷’模式，此文中提到的時間（變量）與線圈溫度（因變量）之間由于受到外界干擾與電機動子線圈運動之間的關系（y電機動子線圈來回往復運動，而吹氣冷卻裝置固定在電機定子上，因此溫度的觀測值受到吹氣裝置的影響，溫度自然會高低起伏），用‘峰谷’模式的數(shù)學模型更加貼合實際。

數(shù)學模型如下：

對于一組容量為n的樣本，假設因變量Y與變量X之間的相關關系滿足：

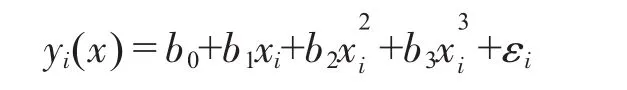
其中yi為觀測的溫度值，而xi為時間變量，εi相互獨立，服從N(0,σ2)分布，代表其它隨機因素影響的總和，其中 i=1，2，….n；

這里采用最小二乘估計，定義：

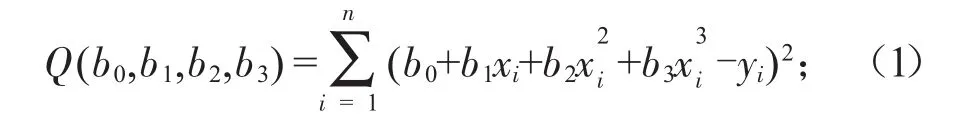
根據(jù)多元函數(shù)求極值的方法令：

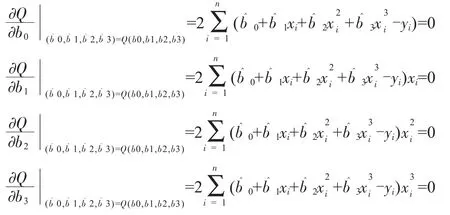
整理的方程組，用矩陣的方法表示如下：

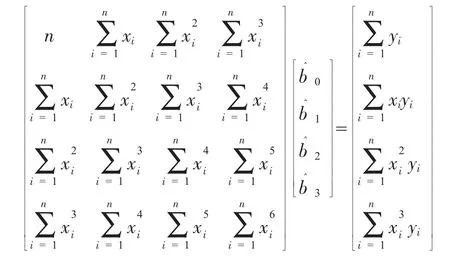
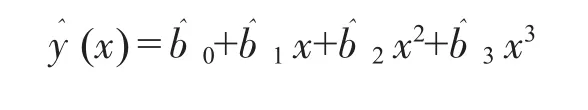
2 電機冷卻系統(tǒng)實驗分析

如圖1所示，是全自動引線鍵合機xy平臺y直線電機的動子線圈部分的細節(jié)圖，在圖中所示的A、B、C三點安置溫度傳感器，運動特性如表1所示。

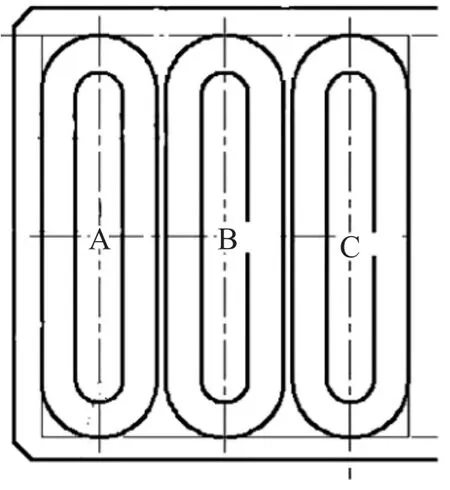
圖1 y向直線電機線圈圖

表1 y向電機運動特性

在吹氣量、加速度、運動距離、運動頻率（來回往復運動）不變的情況下，從14：47開始運動，并測量A、B、C三點的溫度值，每分鐘記錄一次測量溫度值，測量結果如表2所示。表中14：47的溫度值為室溫?？梢钥闯鲩_始運動后，溫度逐漸上升。我們用回歸方法來分析表2中的數(shù)據(jù)。

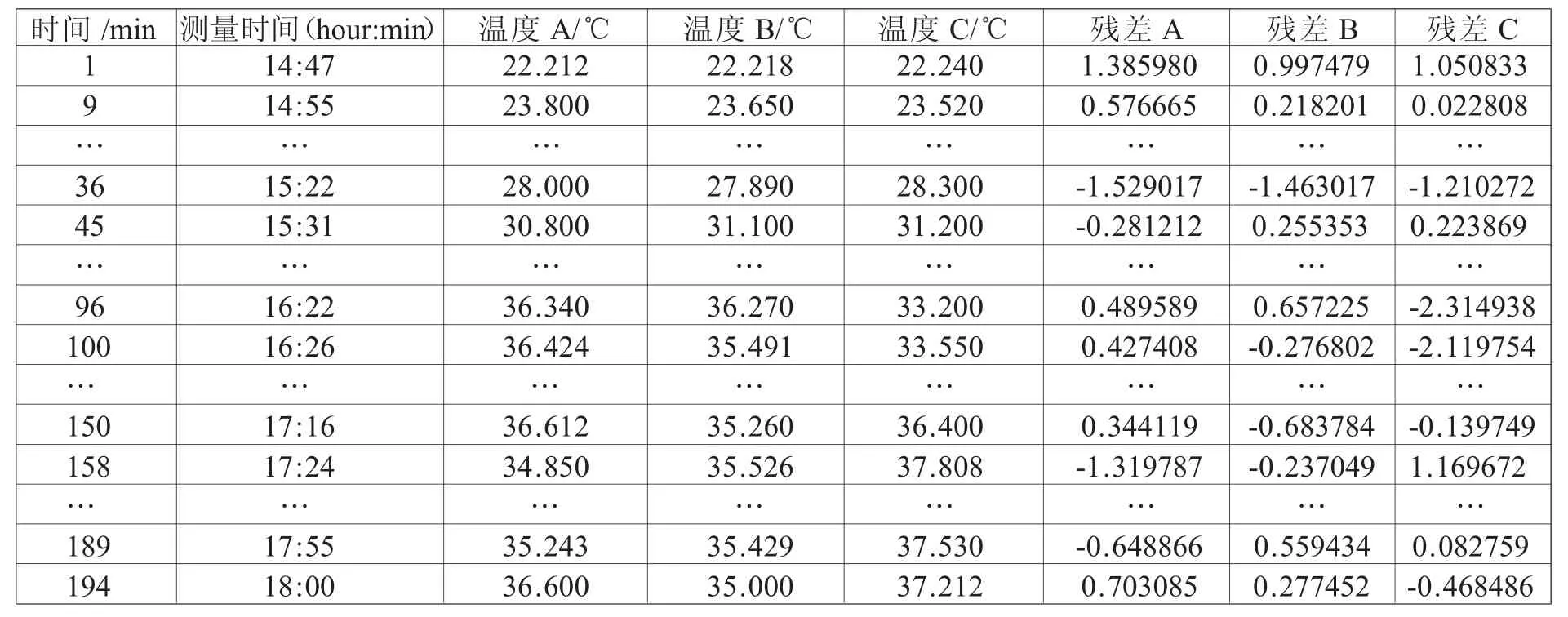
表2 根據(jù)時間測量的溫度值

由于測量點為A、B、C三點，可認為三點相互獨立，分別對三點的溫度與時間進行回歸分析；在數(shù)學模型的基礎上，利用Minitab 軟件，確定回歸函數(shù)系數(shù)與曲線擬合圖。分析結果如下：

（1）多項式回歸:溫度 A（℃）與 時間（min）

根據(jù)數(shù)學模型，計算后的回歸方程為：

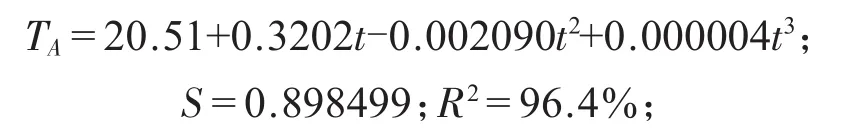
其中TA為線圈A點的溫度值（℃），t為開始工作后的時間（min），圖2為點A處的溫度與時間擬合線圖。

表3 方差分析表

表3中SS為平方和，MS為均方差，DF為自由度，P值是確定否定假設檢驗中原假設的適當性，值的范圍在0到1之間，值越小表明錯誤的否定原假設的概率就越小。R2表示響應變量變異中由其與一個或多個預測變量的關系所解釋的百分比，R2越大，表示模型與數(shù)據(jù)擬合的越好。

圖2 點A處的溫度與時間擬合線圖

以上計算得出，P值為0說明回歸函數(shù)是有意義的，R2的值為96.4%也說明回歸函數(shù)與實驗數(shù)據(jù)擬合的程度非常好。說明回歸函數(shù)是顯著的。這樣就可以利用回歸函數(shù)對A點的溫度根據(jù)xy平臺運行的時間來進行預測。

函數(shù)中的系數(shù)是由樣本估計出來的，因此系數(shù)本身就有波動性，導致由此而來的估計值也有波動性，理論上的預測值與真正的測量值之間有一定的偏離，因此在此引入殘差分析，本文中，殘差的定義可以是：在某時間點處的殘差就是因變量的觀測溫度值與因變量的估計溫度值之間的差值。殘差的分析可根據(jù)殘差圖來分析，如圖3、4所示，根據(jù)相應回歸函數(shù)得到A點殘差圖的直方圖與概率圖。

殘差的概率圖與直方圖表示殘差服從正態(tài)分布，從圖3、4中可知，在y電機線圈A點的測量溫度值與回歸函數(shù)之間的殘差是符合正態(tài)分布的，這也說明了回歸函數(shù)的顯著性。

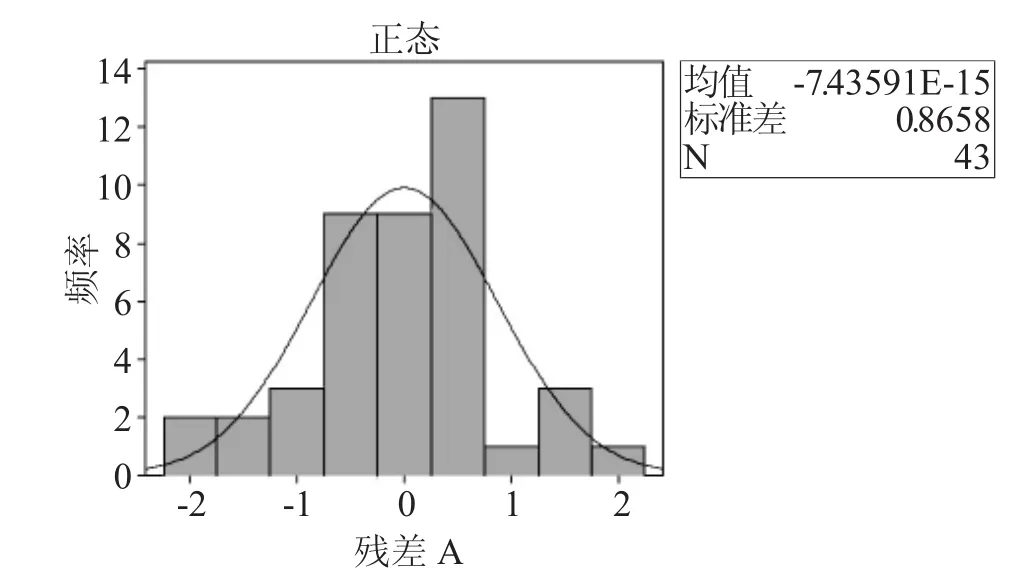
圖3 A點殘差的直方圖

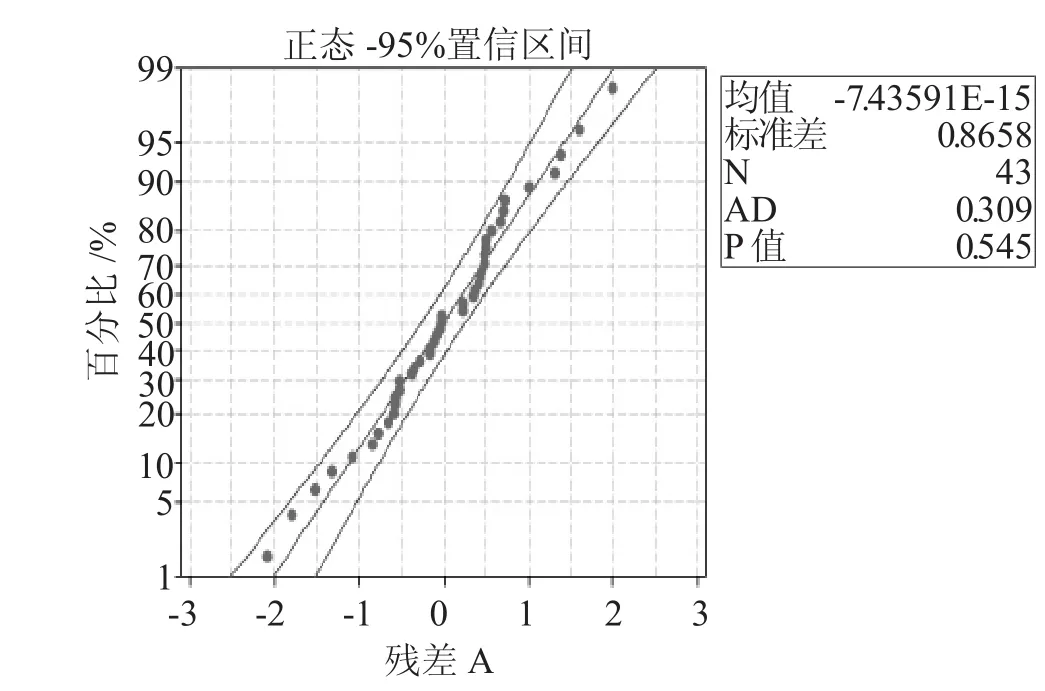
圖4 A點殘差的概率圖

如圖5所示，殘差點在橫軸殘差為0的上下波動著，不存在上升、下降、擺動、跳躍等趨勢，說明在數(shù)據(jù)觀測的過程中沒有受到某個位置因素的強大影響。

從以上殘差圖可以說明，并沒有足夠的證據(jù)使得對A點溫度與運行時間的回歸函數(shù)所做的假定表示懷疑，可以確信，針對A點的觀測數(shù)據(jù)而建立的回歸函數(shù)是合理的。

同理，可以得出測量B點、C點溫度與工作時間的回歸函數(shù)。

(2)多項式回歸:溫度B（℃）、C（℃）與時間（min）

B點處回歸方程如下：

圖5 A點殘差按觀測順序的散點圖

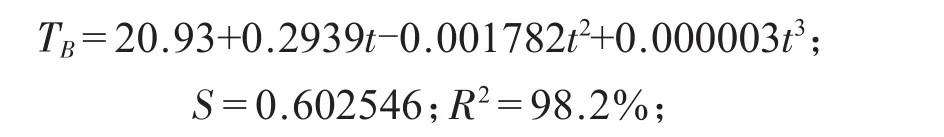
方程中TB為線圈B點的溫度值（℃），t為開始工作后的時間（min），圖6為B點處溫度與時間的擬合線圖。

C點處回歸方程如下：

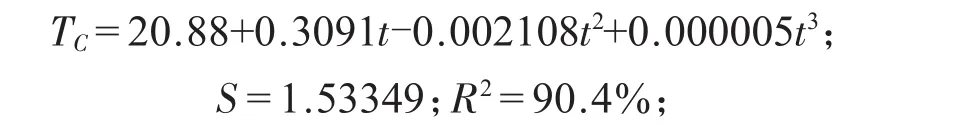
以上方程中TC為線圈C點的溫度值（℃），t為開始工作后的時間（min），圖7為C點處溫度與時間的擬合線圖。

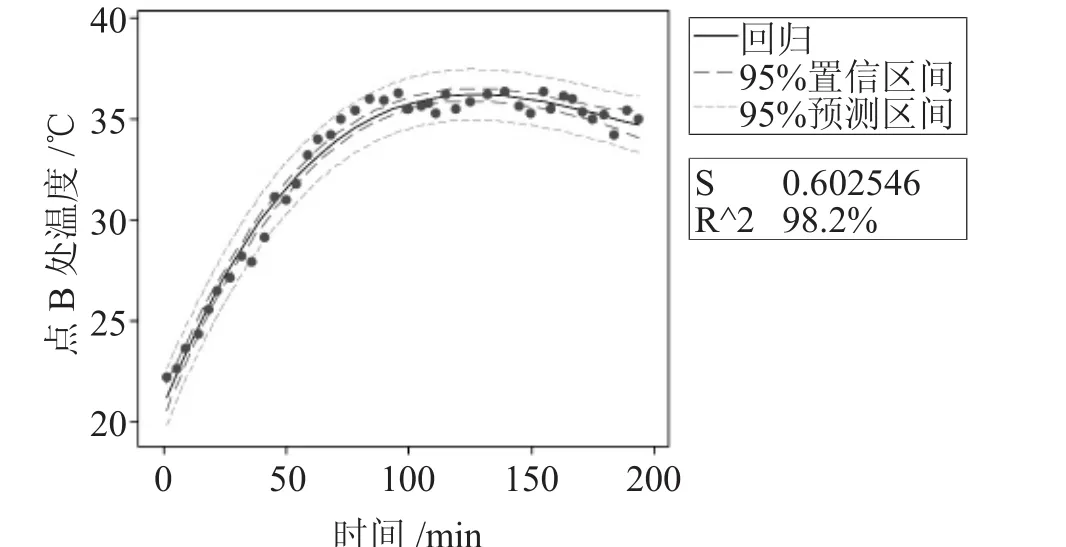
圖6 點B處的溫度與時間擬合線圖

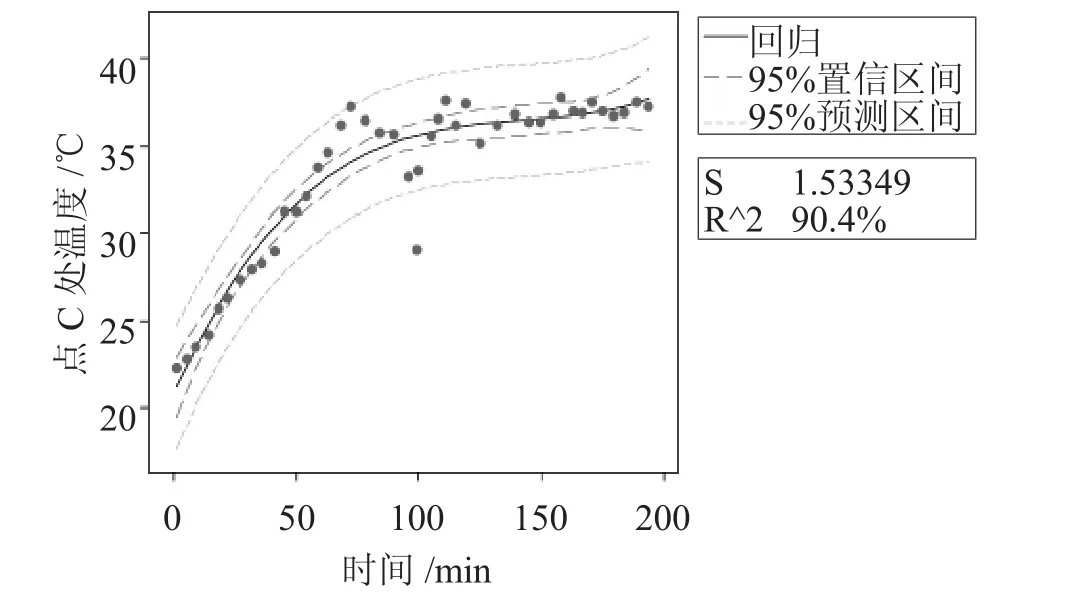
圖7 點C處的溫度與時間擬合線圖

3 結 論

根據(jù)實驗數(shù)據(jù)得來的回歸函數(shù)與擬合曲線，建立了xy平臺y向直線電機工作時間與動子線圈溫度之間的函數(shù)關系，可以預測y電機開始運行后某時間點時動子線圈的溫度范圍，也可以估計線圈在某一溫度范圍時y向電機的大致運行時間，溫升的快慢，多長時間達到熱平衡等。

本文研究了在一定的運動特性條件下xy平臺的y向電機從開始工作的時候的溫升過程，進而為電機以及電機冷卻系統(tǒng)設計提供參考。從實驗數(shù)據(jù)來看，xy平臺的冷卻系統(tǒng)是非常有效的。

當然回歸分析的應用不止可用在建立時間與溫度的關系函數(shù)，也可以設計更多的實驗，用回歸方法研究其它變量之間的關系，如：吹氣流量與運動速度的關系、吹氣流量與加速度的關系等。

[1] 馬 林，六西格瑪管理[M]，北京：人民大學出版社2005.08

[2] 朱學軍、王安麟、黃洪鐘.基于健壯性的機械設計方法[J].機械科學與技術，2000(3):230-233.

[3] 桑桔.Minitab在統(tǒng)計分析中的應用[J].上海統(tǒng)計，2003(12):41-43.

[4] 倪加勛.應用統(tǒng)計學[M].北京:中國人民大學出版社，1993.