金屬材料裂紋擴展Paris律的模擬方法與應用

石凱凱，蔡力勛，黃學偉，姚 迪

（西南交通大學力學與工程學院，四川 成都 610031）

0 引 言

疲勞壽命一直是疲勞研究的核心問題之一。20世紀60年代斷裂力學進入工程領域以來，疲勞裂紋擴展規律的描述公式以Paris模型為代表

式中：a——裂紋長度；

N——循環次數；

ΔK——應力強度因子幅；

C，m——材料常數。

試驗研究和數值模擬是目前研究材料疲勞裂紋擴展速率的主要途徑。試驗方面，國內外學者研究了不同載荷比R、卸載和過載等對材料疲勞裂紋擴展速率的影響[1-3]。數值模擬方面，其研究主要表現為：用材料的疲勞裂紋擴展速率規律預測結構的疲勞裂紋擴展[4-6]；基于多軸本構關系、臨界損傷，預測了材料的疲勞裂紋擴展速率[7]。因數值模擬中采用多軸本構模型，故在模擬計算時有較多人為可調參數，所以對該方法的預測準確度和可靠性還需要進一步研究。該文應用材料低周疲勞（low cycle fatigue，LCF）試驗獲得的Manson-Coffin律，通過有限元分析方法（finite element analysis，FEA）實現了材料疲勞裂紋擴展（fatigue crack growth，FCG）性能的數值模擬，該模擬方法稱為LFF（LCF-low cycle fatigue+FCP-fatigue crack propagation+FEA-finite element analysis）方法。

該文結合Cr2Ni2MoV轉子材料、TA12合金和TC4合金材料的單軸低周疲勞性能數據，通過LFF法和CT試樣對材料疲勞裂紋擴展行為進行分析，將模擬結果與文獻[8]中的疲勞裂紋擴展數據比對，說明LFF法的可行性；之后通過數值模擬給出了N18合金材料不同溫度下I型裂紋的疲勞擴展行為。

1 LFF方法

1.1 LFF方法的機理

描述材料疲勞裂紋擴展速率的Paris公式與低周疲勞Manson-Coffin（M-C）律表征的都是材料塑性疲勞的固有特性，且二者都是基于比例加載獲得；同時在裂紋擴展過程中，裂紋尖端區附近處于小范圍屈服，因此疲勞裂紋的擴展可以認為是材料局部的塑性疲勞造成的，即基于材料低周疲勞試驗獲得M-C律與疲勞裂紋擴展試驗獲得的Paris律應有互通性。鑒于此，文獻[10]提出了LFF方法。

LFF法思路：（1）通過材料低周疲勞試驗獲得相應材料的低周疲勞臨界損傷關系，利用有限元方法得到裂尖塑性區的應力應變場；（2）基于疲勞裂紋擴展模型預測下一次裂紋的擴展方向、擴展尺寸以及相應的循環次數，完成一次疲勞裂紋擴展；（3）根據新裂紋的擴展方向以及尺寸，生成新的有限元網格模型進行下次的疲勞裂紋擴展，依此連續循環，最終獲得表征裂紋擴展速率規律的a-N、da/dN-ΔK曲線。

1.2 基于平均損傷假設的Manson-Coffin損傷律

根據Miner線性損傷累計理論，每循環1周的損傷為D=1/Nf，臨界損傷D0＝1，即當裂尖累計損傷達到臨界損傷D0時，判定裂尖失效。由斷裂力學知道，疲勞裂尖存在應力奇異性，單純根據裂尖的損傷來判定尖端失效是不合理的[10]。

因此，基于有限元計算分析，得到每個加載循環下裂尖塑性區裂紋擴展方向上每個節點的Δε1/2和σ1m，然后結合考慮了平均應力σm和損傷D的M-C律（式（2）），得到每個加載循環下裂尖塑性區裂紋擴展方向上的損傷分布，這便是LFF方法的理論依據。

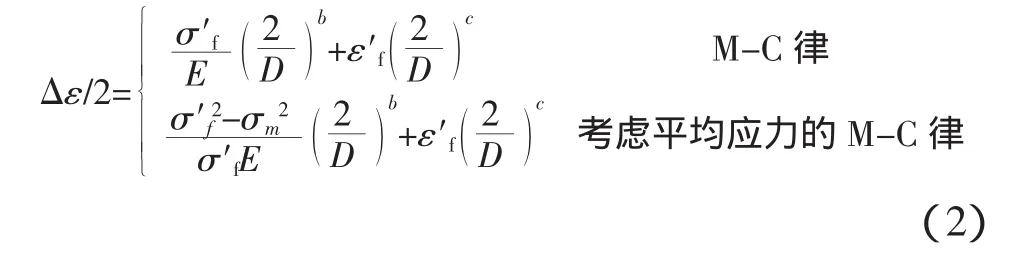
圖1給出了TA12合金CT試樣在初始裂紋a0=12 mm、載荷P=6kN下的裂尖塑性擴展方向上的損傷分布，其中橫坐標r表示到裂紋尖端的距離。由圖1可以看出，距離裂尖越近，損傷越大。

圖1 裂尖塑性區裂紋擴展方向上的損失分布

式中：A——塑性損傷區的面積?

定義平均損傷為；rp（a）——裂紋長度為a時裂紋擴展方向上塑性區的尺寸。

結合Miner線性損傷累計理論，裂紋長度從a擴展到a+rp（a）需要的循環次數N為

通過有限元數值模擬和分析，獲得CT試樣ai+1-Ni+1數據組，獲得a-N曲線；通過割線法數據處理后，即可得到a-da/dN曲線；然后計算得到每個裂紋長度下的應力強度因子幅ΔK，進而建立用來描述材料穩定階段裂紋擴展速率的Paris式（1）。

斷裂力學中，I型裂紋是最主要、最危險的裂紋存在形式，且I型疲勞裂紋擴展方向沿裂尖最大主應變垂直方向擴展。

2 CT有限元模型

采用ANSYS11.0版本有限元軟件進行數值計算。由8節點PLANE82號單元進行網格劃分的平面有限元模型如圖2所示，網格模型共生成了約25 000個單元。由于該文重點關注含I型裂紋CT試樣的疲勞擴展行為，考慮到試樣具有對稱性，故只需對CT試樣的一半建立數值網格模型。如圖2所示，CT試樣的上圓孔頂部施加X方向的位移約束，載荷P在垂向上加到上半弧各個節點上。圖3給出了模型裂尖處的單元細化情況。

3 LFF法預測Paris律的有效性

3.1 氣輪機轉子材料Cr2Ni2MoV鋼（常溫）

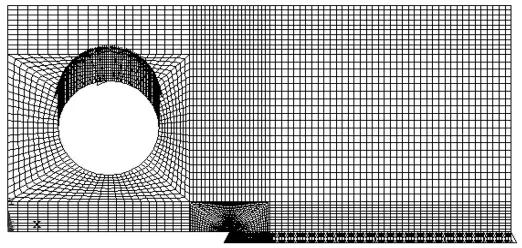
圖2 CT試樣分網情況

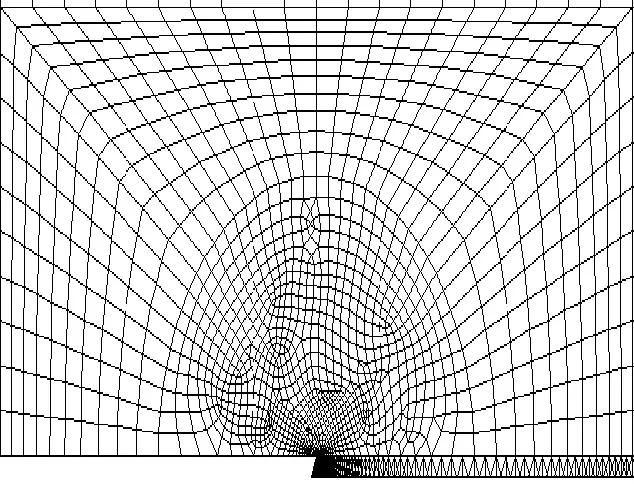
圖3 裂紋尖端分網情況

通過MTS試驗機，獲得轉子材料（常溫）的單軸拉伸力學行能：E=215 000 MPa、Rp0.2=860 MPa、Rm=978MPa。

按照GB/T 15248-2008《金屬材料軸向等幅低循環疲勞試驗方法》，獲得汽輪機轉子材料Cr2Ni2MoV鋼室溫下的低周疲勞ε-N曲線，如圖4所示。圖中，在對數坐標下，應變幅Δε與倍壽命2Nf之間滿足線性關系。根據GB/T 15248-2008分別對lgεe-lg2Nf曲線和lgεp-lg2Nf曲線進行冪率擬合，得到Manson-Coffin 模型的疲勞參數：σ′f=903，b=-0.0404，ε′f=1.101，c=-0.6787。其中 b，σ′f，c 和ε′f分別表示材料的疲勞強度指數、疲勞強度系數、疲勞塑性指數和疲勞塑性系數。試驗獲得的Manson-Coffin模型的疲勞參數是LFF法模擬計算的必要數據。

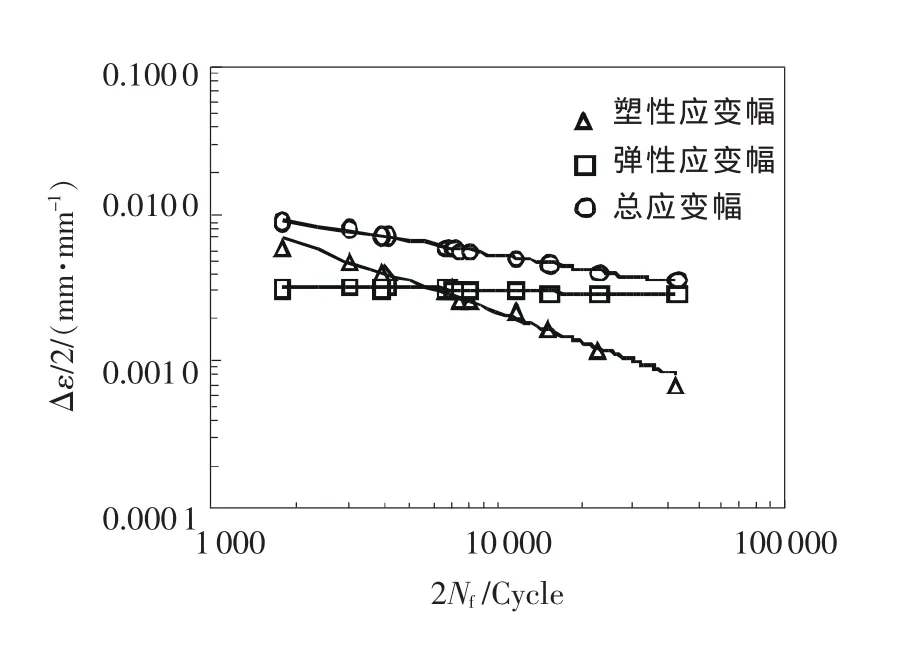
圖4 Cr2Ni2MoV鋼室溫低周疲勞ε-N曲線

根據文獻[11]提供的標準CT試樣構形，采用R=0.1，對轉子材料Cr2Ni2MoV（CNMV）鋼分別建立CT試樣有限元模型。

圖5為試驗結果與LFF法模擬結果在常溫下轉子材料的疲勞裂紋擴展行為即Paris公式的比較圖。為了更直觀地描述數值模擬的預測準確度，圖6給出了疲勞裂紋擴展過程中有限元方法對循環次數的預測準確度，圖6中的每個數據點都是基于相同的裂紋擴展長度得到的。由圖6可以看出，數值模擬的預測準確度基本在1.2倍安全線內。由此可見，LFF方法對于汽輪機轉子材料的裂紋擴展的預測有合理準確度。通過數據處理，得到Paris公式的模擬參數為 C=3.77×10-8，m=2.32。

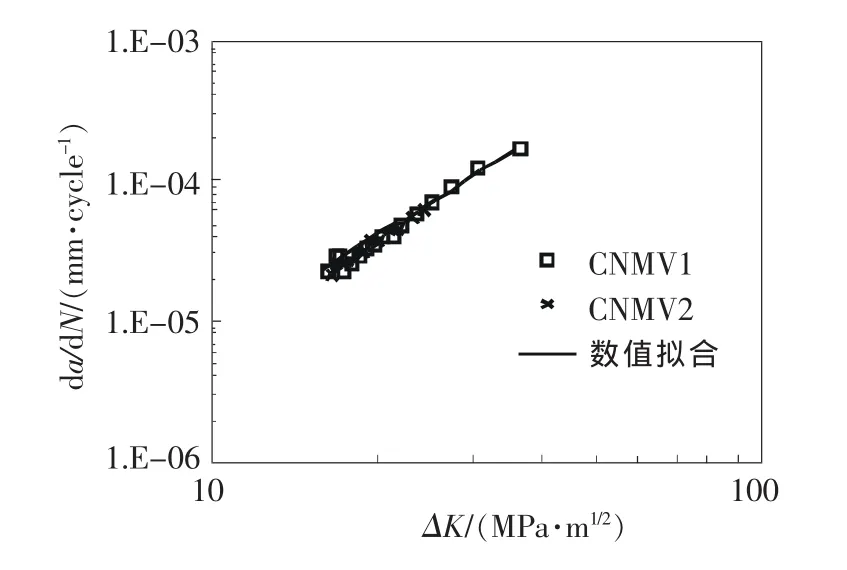
圖5 Paris律的試驗與LFF方法預測結果對比

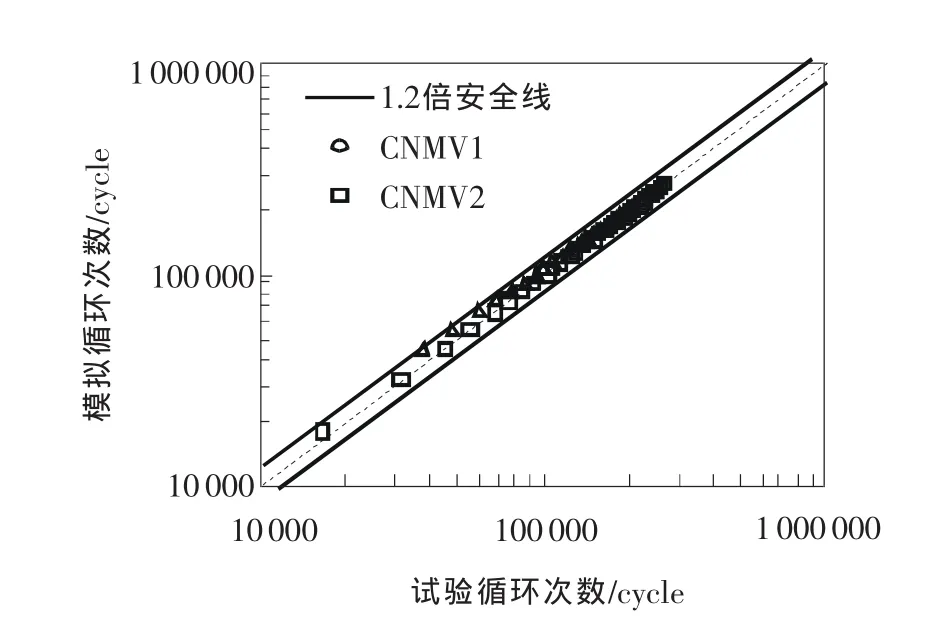
圖6 數值模擬循環次數的預測準確度

3.2 TA12和TC4合金的疲勞裂紋擴展行為模擬有限元結果討論

文獻[8]提供了TA12合金和TC14合金材料常溫下的屈服強度σp0.2（RP0.2）和抗拉強度σb（Rm），見表1。

表1 TA12和TC4合金材料單拉力學性能參量

TA12與TC4合金常溫低周疲勞實驗結果可根據文獻[8]查詢。表2給出了根據實驗數據回歸得到的M-C參數。

表2 TA12和TC4合金低周疲勞性能

圖7給出了TA12與TC4合金的低周疲勞倍壽命2Nf與應變幅Δε/2的關系曲線。由圖可見，在高應變水平下，TA12與TC4鈦合金的低周疲勞損傷程度有較大差別；同時文獻[8]還提供了2種合金材料的疲勞裂紋擴展的Paris律也存在較大差異，由此可推論出高應變水平的低周疲勞損傷差異會對Paris律有一定影響。該文基于LFF方法來實現2種材料Paris律預測，并將數值模擬結果與文獻[8]提供的Paris律進行比對，以驗證LFF方法預測Paris律的有效性。

圖7 TA12、TC4低周疲勞性能曲線

通過查閱文獻[8]和LFF數值模擬獲得TA12和TC4合金材料疲勞裂紋擴展Paris相應參數，見表3。通過LFF法對TA12、TC4合金進行數值模擬，其模擬結果與試驗結果分別見圖8、圖9。從表3和圖8、圖9可以看出，LFF法在模擬材料疲勞裂紋擴展Paris律時，其模擬結果與實驗結果吻合性好，因此LFF方法在數值模擬材料疲勞裂紋擴展方面是有效的。

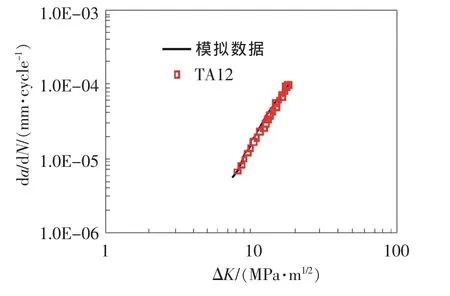
圖8 da/dN-ΔK曲線的有限元結果與試驗對比

圖9 da/dN-ΔK曲線的有限元結果與試驗對比

表3 TA12和TC4合金材料試驗Paris公式參數

4 LFF方法的應用實例

4.1 轉子材料不同溫度下的疲勞裂紋擴展行為

對轉子材料疲勞行為研究除了常溫之外，還應考慮轉子高溫情況下材料的疲勞裂紋擴展行為。圖10給出了轉子材料常溫（20℃）與高溫（300℃）下的本構關系。從圖10可以看出轉子材料在高溫300℃下材料的屈服應力Rp0.2以及抗拉強度Rm都有不同程度的下降。

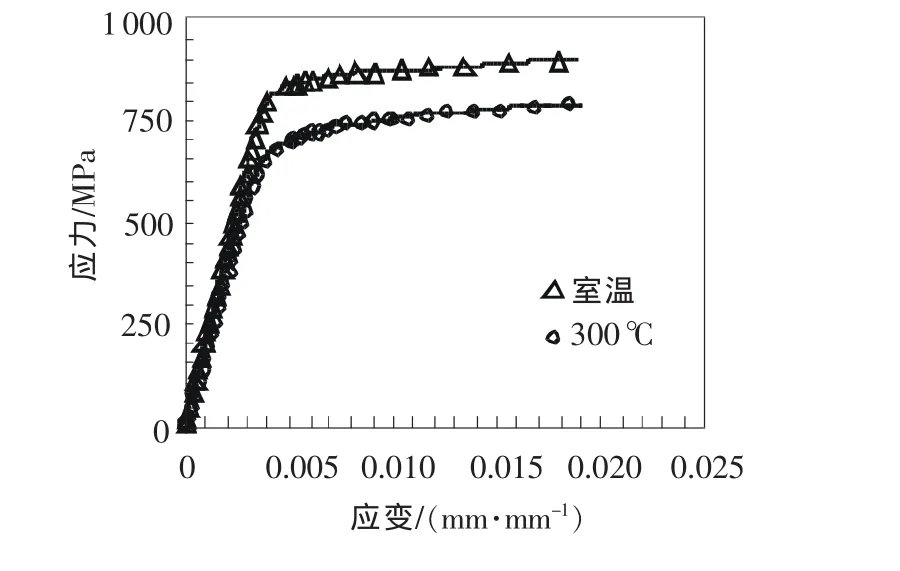
圖10 Cr2Ni2MoV鋼單軸拉伸曲線與R-O模型

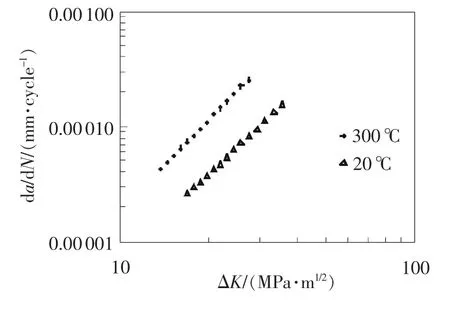
圖11 轉子材料常溫與高溫疲勞行為

圖11給出了轉子材料常溫與高溫情況下材料的疲勞擴展行為。可以看出，溫度的升高會加快轉子材料的裂紋擴展。轉子材料Cr2Ni2MoV鋼在300℃下的 Paris律的參數：C=5.24E-08，m=2.573。

4.2 Zr-Sn-Nb合金不同溫度下的疲勞裂紋擴展行為

Zr-Sn-Nb合金（N18鋯合金，用于核反應堆燃料包殼材料）材料在不同溫度下的疲勞行為有重要工程意義。限于試驗條件，高溫下N18材料的裂紋擴展行為的試驗成果在國內尚無報道。該文通過LFF方法完成了轉子材料、N18合金的疲勞裂紋擴展模擬，給出了Paris律，供工程參考。

圖12給出了LFF方法對N18合金在不同溫度下的疲勞裂紋擴展速率與應力強度因子幅度的模擬關系。從圖12可以看出，N18合金在不同溫度下材料的疲勞裂紋擴展行為存在差異，在20℃和200℃下疲勞裂紋擴展速率比較接近（溫度200℃時的循環變形特性與室溫相同[12]），但在400℃（鋯合金包殼在水冷動力堆中的工作溫度）、450℃和500℃的高溫情況下疲勞裂紋的擴展速率卻表現出明顯差異，溫度越高擴展速率提高越顯著。表4給出了5種溫度工況下N18的Paris公式的參數。

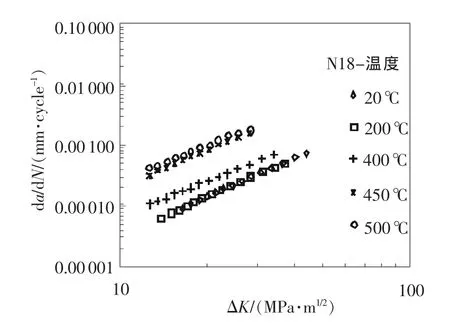
圖12 N18不同溫度下疲勞裂紋Paris律

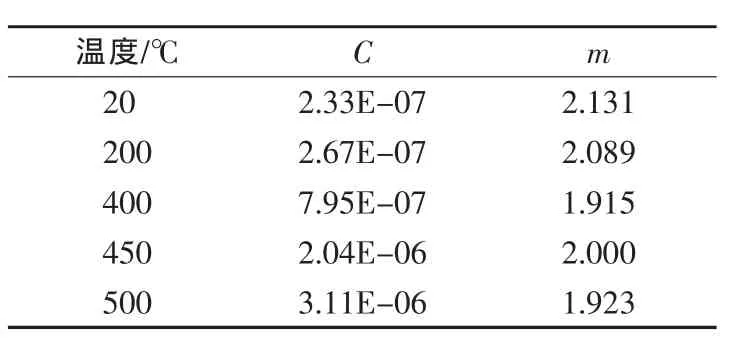
表4 5種溫度下N18鋯合金Paris模型參數

5 結束語

LFF方法對TA12鈦合金、TC4鈦合金和轉子材料Cr2Ni2MoV鋼的Paris律有良好的模擬準確度，證明了LFF方法的有效性。

應用LFF方法模擬了Cr2Ni2MoV鋼和N18鋯合金在高溫下的I型裂紋Paris模型參數，可以看出溫度對2種材料的疲勞裂紋擴展速率有一定影響，且隨著溫度的升高，其材料的疲勞裂紋擴展速率增大。

[1]Huang X P，Moan T，Cui W C.An engineering model of fatigue crack growth under variable amplitude loading[J].International Journal of Fatigue，2008（30）：2-10.

[2] Zhao T W，Zhang J X，Jiang Y Y.A study of fatigue crack growth of 7075-T651 aluminum alloy[J].International Journal of Fatigue，2008（30）：1169-1180.

[3] Kalnaus S，Fan F，Vasudevan A K，et al.An experimental investigation on fatigue crack growth of AL6XN stainless steel[J].Engineering Fracture Mechanics，2008（75）：2002-2019.

[4] Schollmann M，Fulland M，Richard H A.Development of a new software for adaptive crack growth simulations in 3D structures[J].Engineering Fracture Mechanics，2003（70）：249-268.

[5]Furukawa C H，Bucalem M L，Mazella I J G.On the finite elementmodeling offatigue crack growth in pressurized cylindrical shells[J].International Journal of Fatigue，2009（31）：629-635.

[6] 蔡力勛，包陳，金蕾.金屬材料斷裂力學柔度測試技術的問題與發展[J].中國測試，2009，35（1）：9-18.

[7] Fan F F，Kalnaus S，Jiang Y Y.Modeling of fatigue crack growth of stainless steel 304L[J].Mechanics of Materials，2008（40）：961-973.

[8]《工程材料實用手冊》編輯委員會.工程材料實用手冊第4卷[M].北京：中國標準出版社，2006：59-131.

[9] 黃學偉.新結構材料力學行為的獲取方法[D].成都：西南交通大學，2010：44-48.

[10]姜鳳華，田常錄.疲勞裂紋擴展的數值模擬[J].內蒙古工業大學學報，2004，23（3）：161-166.

[11]GB/T 6398—2000金屬材料疲勞裂紋擴展速率試驗方法[S].北京：中國標準出版社，2000.

[12]連姍姍，譚軍，馮可芹，等.N18鋯合金的低周疲勞行為[J].原子能科學技術，2009，43（12）：1118-1122.