有限周期結構的漏泄電纜電特性研究

和 晨，喻志遠，郭麗麗，袁衛文

（1.電子科技大學應用物理所，四川 成都 610054；2.中天日立射頻電纜有限公司，江蘇 南通 226010）

0 引 言

漏泄同軸電纜（leaky coaxial cable，LCX），簡稱漏纜，是移動通信系統中用來代替天線，改善特定區域內電磁波場強的一種導波結構。在LCX的理論研究和應用方面，國內外的研究人員在分析漏泄同軸電纜場分布時常用的方法是模式匹配法[1-4]。

該文目的是研究在多個縫組的漏纜的開縫形式中，相鄰開縫組之間的耦合效果與距離之間的關系。漏纜的電磁仿真受到計算機內存空間的限制，只能從有限長度的漏纜來推算較長漏纜的電參量（如50m）。但是這種方法忽略了漏纜中縫與縫之間的耦合，由此產生的誤差使得仿真得到的結果不可信。因此有必要對漏纜中開縫間的耦合進行認真的研究，以找到可以消除縫間耦合的影響研究方法。

1 LCX主要電參量定義

傳輸損耗是描述電磁波能量在漏泄電纜內部傳輸過程中損耗程度的物理量，也是漏泄電纜的關鍵指標之一。漏泄電纜的內導體一般選用銅管，外導體通常選用薄銅片卷制而成，內外導體間填充絕緣介質的相對介電常數不為零。另外，在電纜的外導體上所開槽口，可以使一部分電磁能量從電纜內部輻射到外部空間，因此，漏泄電纜的傳輸損耗一般包括3部分：（1）導體損耗；（2）介質損耗；（3）輻射損耗。

式中：α——漏泄電纜的傳輸損耗；

αc——漏泄電纜的導體損耗；

αd——漏泄電纜的介質損耗；

αr——漏泄電纜的輻射損耗。

耦合損耗（loss couple）是表征漏泄同軸電纜輻射能力和接受能力強弱的綜合指標，也是漏泄同軸電纜有別于普通同軸電纜的唯一指標。耦合損耗的定義為：

式中：Pr——距離電纜1.5m或2m的標準半波偶極子天線接收到的功率；

Pt——與天線正對處漏泄電纜中傳輸的功率。

耦合損耗的大小與移動接收機和漏泄電纜之間的距離有直接的聯系，還與電纜的工作頻率和槽口的排列方式、尺寸以及形狀有密切的關系。

2 LCX縫間耦合效果與距離關系的相關理論

對于周期結構，根據文獻[5]中的弗洛奎定理可知，如果 z1=z，z2=z+Δz，則

對于周期系統，系統沿z方向相距為空間周期p的m倍的2個截面上，Δz=mp，m為整數，有

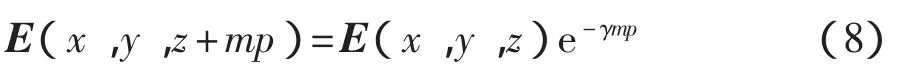
對于非均勻系統，場在橫截面的分布是z的函數，則

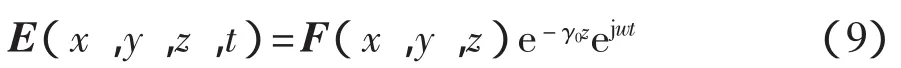
對于周期系統，F（x，y，z）對于 z是一個周期函數，有

即系統中的z向相距為mp的2個橫截面上的場有

研究表明，對于LCX中的任意開縫，不但有電磁能量向外輻射，而且還有由于開縫間的耦合而產生的電磁能量的輸入。由有限長的LCX來推算較長LCX的電特性時忽略了開縫之間的耦合，由于縫間耦合的影響，所得結果中的誤差是不可接受的，因此弗洛奎定理在這里不適用。

根據文獻[6]中的惠更斯原理公式，如果Js=n×H，Ms=-n×E，則

且有

則可以得到

其中

3 關于LCX縫組間耦合的仿真研究

為了研究LCX中縫間耦合的電磁特性，用CST軟件對其進行仿真。在仿真中取內外導體為完善金屬，并取其中的介質是無耗的，這樣參量僅與開縫的電磁輻射相關。

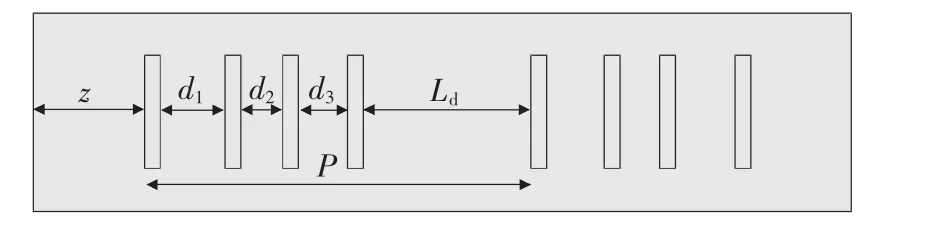
圖1 新型開槽LCX模型

圖1為參考文獻[7]提出的新型開槽漏泄同軸電纜的結構。其基本單元是由一組互相接近的非周期性槽孔組成。基本單元在電纜上以周期P重復，把周期P設計得很大，使得基本單元之間的干擾可以忽略。如上所述，鄰近的縫間干擾是不可忽視的。在一個基本單元中第i個槽孔之間的距離di和周期P可以用遺傳算法優化得到最理想的耦合損耗結果。槽孔長為a，寬為b。這里取Z=50mm，d1=32.7mm，d2=10.9 mm，d3=21.8 mm，a=17 mm，b=4mm。

由仿真可得到圖2。

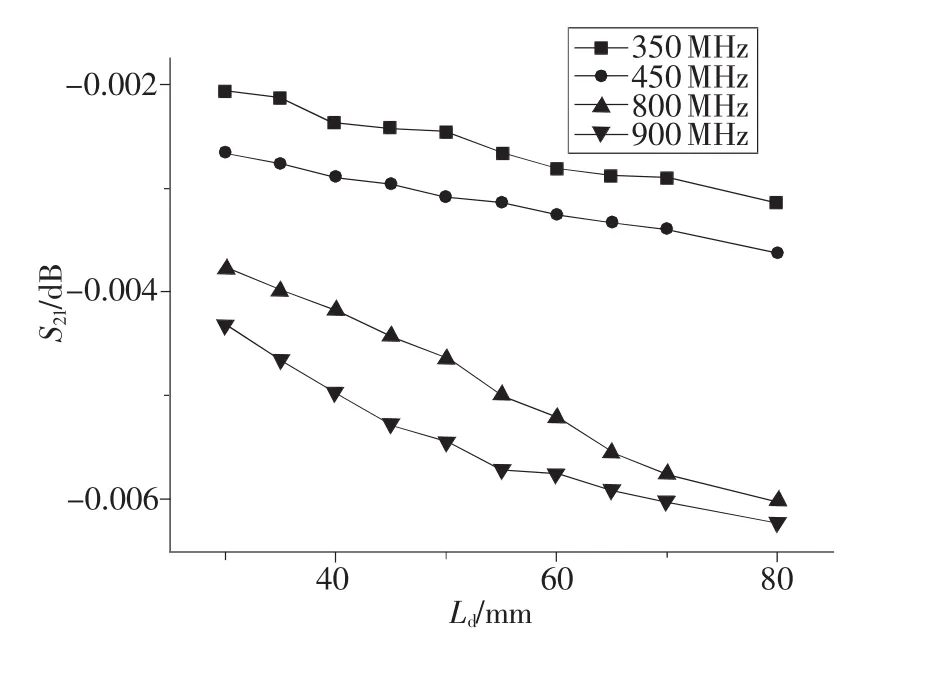
圖2 4種要求的頻率下耦合損耗隨縫組間距離的變化情況

由圖2可知，隨著縫組間距離的增大，縫組的耦合效應呈減小的趨勢。

由圖3可知，以900MHz的頻率為例，隨著開縫組間距離的增大，開縫組的耦合損耗呈越來越小的趨勢。這種情況證實了惠更斯原理的定義。

令Lmin為此最小的縫間或縫組之間的距離，則從定性的分析可以知道，Lmin與以下的因素相關：

（1）開縫的同軸電纜的尺寸大小，即與同軸電纜的型號相關。

（2）與縫或縫組的結構形式和尺寸相關。

（3）與LCX的工作頻率相關，即Lmin應該是工作頻率的函數。

4 LCX的最小縫組間距的求法及舉例

圖3 頻率為900MHz時3種不同規格的LCX隨縫組間距離增大的耦合損耗變化情況

研究目標就是要研究在給定電纜的型號和開縫尺寸結構的前提下，求出可忽略縫間耦合的最小距離Lmin的具體大小，并研究它與開縫結構和工作頻率的關系。

顯然，這里N的大小是一個重要的值。可以參考安德魯公司的U型槽的間距以推算出N，或者參考文獻[7]中的結果，來確定N的值。當頻率不變時，修改以上仿真中的縫或縫組的尺寸，再求Lmin，以研究Lmin與縫的尺寸的關系。當開縫尺寸不變時，改變工作頻率，研究Lmin如何改變。

在以上研究的基礎上，求出滿足指標要求的多頻點LCX結構。

對于給定長度的LCX，如果Ld太大，開縫數目將變少，則耦合損耗必然變小；如果Ld太小，縫或縫組間的耦合將變得不可忽略，也不利于設計。所以能夠忽略耦合損耗的最小Ld，即為所要求的Ldmin。在此，為了簡化研究的過程，暫時忽略非相鄰縫組之間的耦合效果。

現在以17.3～43mm的LCX在900MHz頻率的情況下為例。使用ORIGIN軟件的擬合公式法，令

可以用y′來表示耦合損耗隨縫組間距離的增大而減小的趨勢

則開縫組的一個周期的長度為s=4·b+d1+d2+d3=4×4+32.7+10.9+21.8=81.4 mm，參考安德魯公司的U型槽LCX的開縫方式中，開縫間距Ld=22.7mm。代入計算可得N的參考值為

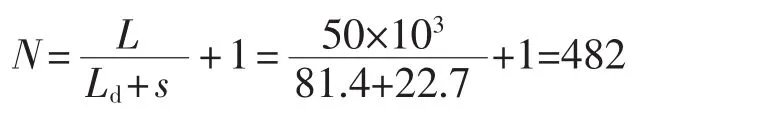
則在50m的電纜中，開縫組的組數為482。如果開縫周期的個數不同，則同樣長度LCX開縫組數會變化，所以這里統一以N=482作為數據誤差的標準。代入式（22）可得

經過數學推導，給出17.3～43 mm規格的LCX在900MHz頻率下，各種開縫間距離的擬合公式，目的是通過討論來得出符合要求的最小耦合距離。經過代入計算，得到圖4。

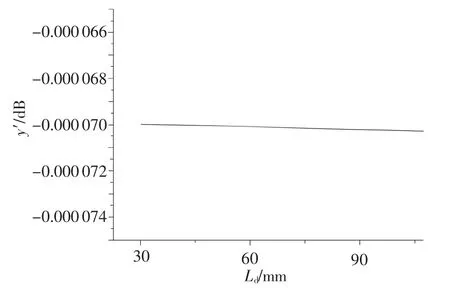
圖4 17.3～43 mm規格的LCX在900MHz的頻率下耦合損耗y′隨縫間距Ld的變化規律

由圖4可知，隨著距離增加，y′基本為一水平線，也就是說耦合損耗隨距離的增加直線下降。

根據式（25），分別代入Ld=20～100mm的仿真結果。可以得到當Ld=50mm時，；而當Ld=60mm時，，可以滿足實際應用中的需要。所以得出此時的Ld=60mm可以作為Lmin。

5 結束語

由仿真結果可以看出，隨著LCX的頻率和縫組間距離的增大，縫組間的耦合效果會越來越小。為了簡化研究的過程，只考慮了相鄰縫組之間的耦合效果。提出的新型開槽LCX模型中，如果采用安德魯公司的U型槽模型的開槽間距代入仿真結果，可以得到最小的縫組間距為60 mm，這個距離可以滿足實際應用的需要。

[1] 彭桂利，葛萬成.漏泄同軸電纜在建筑物內無線通信中的應用[J].光纖與電纜及其應用技術，2005（2）：37-39.

[2]Kim D H，Eom H J.Mode-matching analysis of axially slotted coaxial cable[J].IEEE Antennas and Wireless Propagation Letters，2005（4）：169-171.

[3] Kiang J F.Radiation properties of circumferential slots on a coaxial cable[J].IEEE Transactions on Microwave Theory and Techniques，1997，45（1）：102-107.

[4] Hassan E E.Field solution and propagation characteristics of monofilar-bifilar modes of axially slotted coaxial cable[J].IEEE Transactions on Microwave Theory and Techniques，1989，37（3）：553-557.

[5] Ramo S，Whinnery J R，Theodore V D.Fields and wavesin communication electronics[M].New York Chichester Brisbane Toronto Singapore，1984：615-616.

[6] Zhang K， LiD J.Electromagnetic theory formicrowaves and Optoelectronics[M].Springer-Verlag Berlin Heidelberg，2008.

[7] Wang H S，Gu G Z，Qiao S，et al.Design of leakywave coaxial cable compatible for both 2G and 3G wireless communications[J].Electromagn Waves and Appl，2008（22）：731-740.

[8] 喻志遠.迭代計算中的Thita算法[J].微波學報，1994，5（增刊）：163-165.