基于擴展卡爾曼濾波的輪式移動機器人定位技術

李昌明，梅 莉，秦東興

（1.電子科技大學，四川 成都 611731；2.克拉瑪依職業技術學院，新疆 獨山子 833600）

0 引 言

由于傳感器都存在著自身缺陷，獲取的信息量有限，單一傳感器信號難以保證輸入信息的準確性、可靠性及充足性。針對這個問題，該文采用擴展卡爾曼濾波進行多傳感信息融合，擴展卡爾曼濾波器（EKF）具有收斂速度快、存儲量小的優點[1]。其中里程計、陀螺儀、激光雷達為主要傳感器，將相對定位[2]與絕對定位[3]進行組合，里程計與陀螺儀的融合濾波作為機器人運動學模型；通過激光雷達獲取環境特征，建立其模型作為機器位置觀測模型。運動模型與觀測模型進行結合，利用擴展卡爾曼濾波對環境特征進行跟蹤，最終實現機器人的精確定位。

1 系統工作原理

圖1為設計的擴展卡爾曼濾波機器人定位系統的原理圖。由圖可知，該系統的過程為一個遞推過程。第一步位置預測或動作更新，把高斯誤差運動模型[4]直接應用到機器人所測量的里程計與陀螺儀的行走，獲取里程計和陀螺儀的數據，通過里程計和陀螺儀的估計融合，產生機器人的預測位置。然后根據預測位置，在環境地圖數據庫中找到與之匹配的預測觀測值，即預測激光雷達將提取到的環境特征及特征的位置信息。在匹配過程中，機器人將預測的觀測值與激光雷達的實際觀測值進行匹配，找出最佳匹配。最后應用擴展卡爾曼濾波將最佳匹配所提供的信息進行數據融合，更新估計機器人的信任度狀態，得到機器人位置的最佳估計，最終實現機器人基于環境地圖定位的精確定位[5-6]。

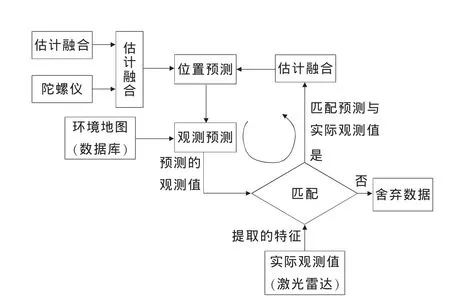
圖1 系統工作原理圖

2 傳感器模型

2.1 里程計模型

建立機器人運動二維坐標地圖，移動機器人的姿態可以表示為

式中：x，y——機器人相對坐標原點的X和Y方向運動距離；

θ——機器人自身姿態相對于X軸角度。

差動驅動機器人的運動模型[7]如圖2所示，在極短固定采樣時間Δt內p到p′機器人位姿改變量（Δx，Δy，Δθ）為

式中：Δsr、Δsl——左右輪行走的距離；

b——兩差動驅動輪之間的間距。

圖2 差動驅動機器人的運動學模型

由此，更新過的位置p′為

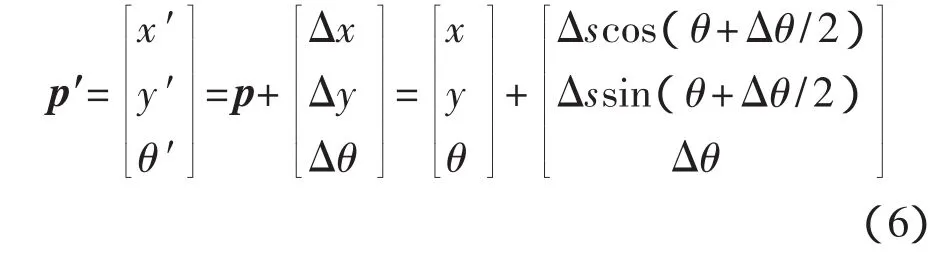
式（6）為里程表位置更新的基本方程。在增量運動（Δsr，Δsl）中，存在傳感器不確定性積分誤差和近似運動模型帶來的誤差。由誤差傳播理論，里程表位置估計的協方差矩陣Σp′為

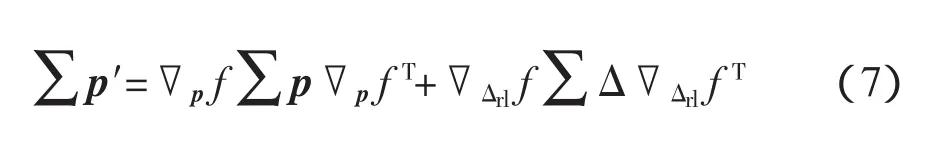
假定初始點協方差矩陣Σp已知，運動增量（Δsr，Δsl）協方差矩陣為

式中：kr、kl——誤差常數，代表驅動電機、輪子和地面交互的非確定性參數，其具體值應由實驗確定。

利用式（6）可以計算2個雅可比矩陣Fp和FΔr1。

2.2 陀螺儀模型

陀螺儀是一種慣性器件，用于測量其載體的轉動角速度和轉動角度，其輸出經積分得到機器人的位姿角度變化量。因此，使用陀螺儀時首先給定一個基準方向，機器人運動中的姿態將由自身角度變化量的不斷累加得到。一定時間Ts內更新過的姿態角 θ′為

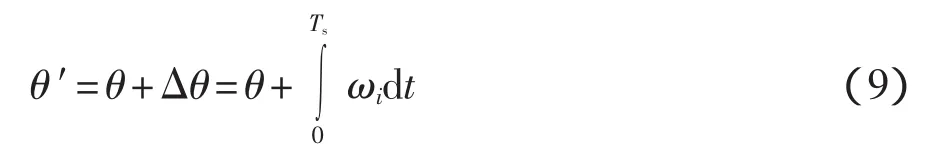
式中：θ——未更新時的姿態角；

ωi——陀螺儀的輸出角速度。

該文假定陀螺儀的測量值服從高斯白噪聲分布，對零輸入時建立擬合誤差模型，確定模型參數，最后求出方差Q（K）。

2.3 激光雷達模型

如圖3所示，在機器人傳感器所處的極坐標中，產生n個測量點xRi=（ρRi，θRi），假定距離信息ρR和掃描角度信息θR的測量誤差受高斯概率密度曲線的約束，方差分別為常量（σρ，σθ），且彼此獨立。給定測量點（ρR，θR）計算相應的歐氏坐標為

xR=ρRcosθR， yR=ρRsinθR

給定一條直線方程為

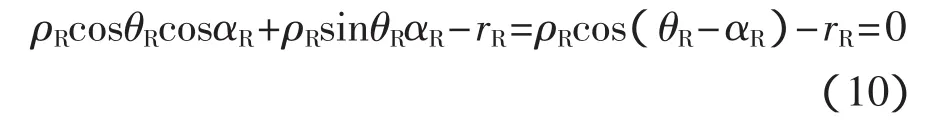
特定點xRi=（ρRi，θRi）到直線之間的正交距離dRi為

圖3 最小平方意義的估計直線及環境坐標W到機器人坐標框架R位置表示

將屬于同一條直線的數據點歸并成類，并采用最小二乘法進行直線擬合，最后得出擬合直線參數αR和 γR。

激光雷達傳感器測量的不確定性將影響所提取直線的不確定性。用A和E分別表示隨機輸出變量αR和γR，系統輸出協方差矩陣為

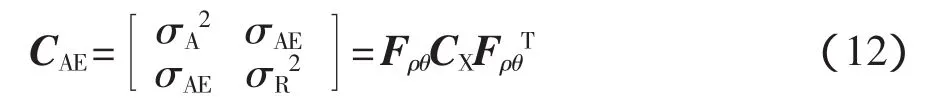
式中：CX——給定2n×2n輸入協方差矩陣，即

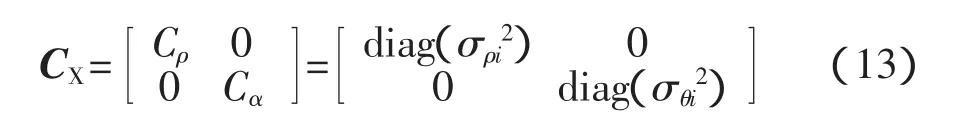
Fρθ——雅可比。

因此，在考慮激光雷達傳感器數據誤差的基礎上，根據提取的直線環境特征建立了傳感器模型。從傳感器數據提取的每一條直線，都有一對參數（αW，rW）和其對應的誤差協方差CAE與其對應，該協方差就是觀測方程中的觀測誤差方差Σ

R，i。

3 環境特征的預測

多傳感融合中最重要的就是測量預測環境特征與觀測環境特征之間的匹配。預測的機器人位置p?（k|k）將產生期望特征 zt，i。在環境地圖中，存儲的特征是直線特征，以環境坐標系參數給出。而傳感器所提取的直線特征是以機器人自身局部坐標給出，因此需要將環境坐標系W中的測量預測特征變換到機器人框架R中，變換由式（14）給出

它的雅可比▽hi為

由機器人預測的位置，機器人框架下可能提取的環境特征被獲取。根據擴展卡爾曼濾波可以得出觀測方程為

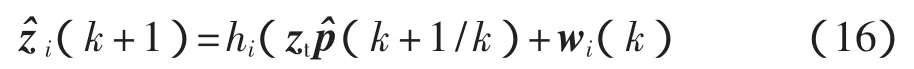
式中：wi（k）——傳感器的觀測誤差。

4 擴展卡爾曼濾波器原理

卡爾曼濾波器是一種基于概率模型進行狀態和參數估計的有效方法，由一系列遞歸數學公式描述。它們提供了一種高效可計算的方法來估計過程的狀態，并使估計均方誤差最小?？柭鼮V波器應用廣泛且功能強大，它可以估計信號的過去和當前狀態，甚至能估計將來的狀態，即使并不知道模型的確切性質。擴展卡爾曼濾波器（EKF）用于處理觀測變量與過程的關系是非線性的問題，首先對其進行線性近似，再利用線性系統卡爾曼濾波器的基本方程實現狀態估計。在移動機器人位姿估計中，在系統噪聲和測量服從高斯白噪聲分布情況下，卡爾曼濾波用帶有噪聲的狀態議程和觀測議程遞推決定統計意義上的最優位姿估計。

5實驗

該實驗平臺為ARM8962 32位ARM Corte-M3主控芯片，協處理器DSP作為數據處理單元進行控制的輪式自主機器人。根據實驗模型，機器人上同時安裝了內部傳感器光電編碼器、陀螺儀和外部環境傳感器激光雷達。激光雷達采用SICK LMS200，該傳感器能對0～180°范圍進行掃描，返回環境測量點距離信息和角度信息。

如圖4所示，實驗在走廊通道中進行，建立機器人運動環境地圖。在O點上建立環境坐標系，路徑規劃機器人由起始位置A移動到終點C，行走距離20 m。機器人移動速度為1m/s，采樣時間控制為0.5 s，估計初始置 A（x，y，θ）為（0，0，0）。為驗正算法收斂性，實際A一定程度偏離原點。

機器人移動過程中采用上述擴展卡爾曼濾波多傳感融合算法進行定位。在B點給出機器人位置預測（細線）與測量（粗線），以及修正融合后得到的機器人位置更新估計（粗虛線）。機器的位置預測、測量及最新估計都存在不確定性，因此機器人的位置以橢圓表示。機器人預測與觀測的特征匹配中采用Mahalanobis距離[8]進行判斷，找出相應匹配。機器人采用線性控制算法進行路徑跟蹤。

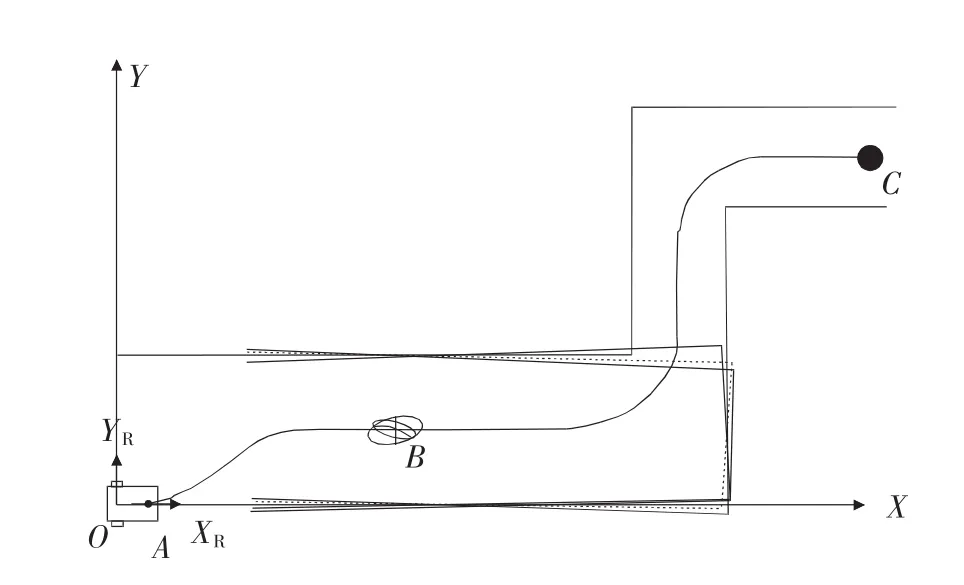
圖4 機器人行走路徑

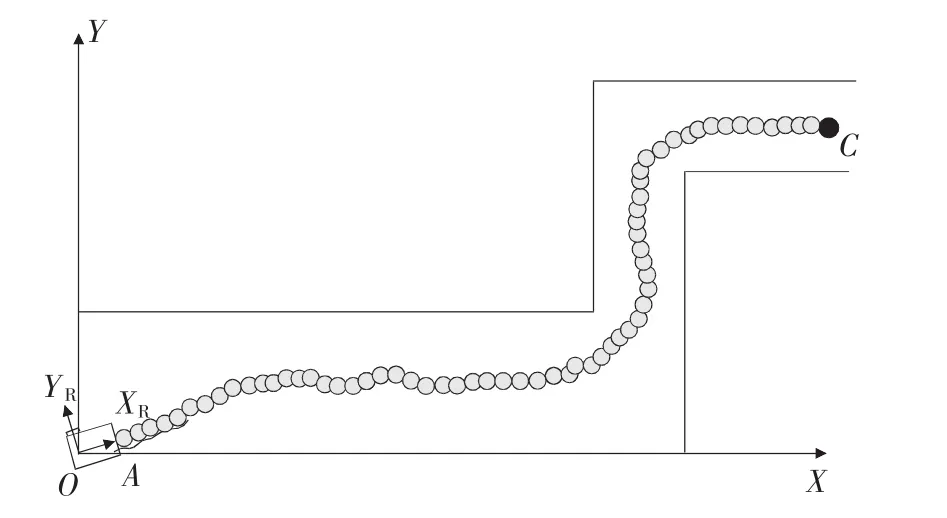
圖5 實驗中機器人行走路線圖

圖5給出實驗中機器人完整行走路線圖。機器人按要求達到目的地，每個位置的定位均方差在2 cm左右，航向角小于0.5rad。實驗結果表明，上述多傳感融合系統的對機器人的導航起到改進作用。

6 結束語

采用擴展卡爾曼濾波算法作為機器人移動中的定位方法，克服了以往單一傳感器或多傳感系統系統誤差表達方式的缺點。將該定位方法應用到實際機器人導航定位當中，能有效提高機器人定位精度，提高機器人定位的可靠性，具有一定的實際應用。

[1] 何子述，夏威.現代數字信號處理及其應用[M].北京：清華大學出版社，2009：250-350.

[2]吳偉，劉興剛，王忠實.多傳感器融合實現機器人精確定位[J].東北大學學報，2007，28（2）：161-164.

[3]楊柏勝，姬紅兵.基于卡爾曼濾波的被動多傳器融合跟蹤[J].控制與決策，2008，23（4）：460-463.

[4] 楊國勝.基于多傳器融合的移動機器人定位與導航研究[D].北京：中國科學院自動化研究所，2004.

[5] 徐立.基于信息融合的機器人定位及地圖創建研究[D].綿陽：西南科技大學，2009.

[6] 孫鐵波，劉奎武，李宏.基于模糊控制的機器人尋線控制系統改進設計[J].電子設計工程，2009，17（11）：32-33.

[7] Siegwart R，Nourbakhsh I R.自主移動機器人導論[M].西安：西安交通大學出版社，2006：225-300.

[8] Jetto L.Development and experimental validation of an adaptive extended kalman filter for the localization of mobile robots[J].IEEE Trans.Robotics and Automation，1999，15（2）：219-229.