基于單軸氣浮臺的角動量輸出測量方法

田留德，趙建科，薛 勛，張周峰，龍江波，段亞軒

（中國科學院西安光學精密機械研究所，陜西 西安 710119）

0 引 言

在軌運行的航天器處于空間微重力環境下，對外是一個獨立的系統，整個系統基本不受外力矩作用，系統角動量守恒[1]。航天器上任何一個部件角動量的變化都會給整個平臺帶來擾動，研究和測量轉動部件的角動量輸出對航天器姿態控制設計具有重要指導意義。如衛星姿態控制系統設計時，需要對各個飛輪的角動量輸出以及多個飛輪的耦合輸出進行精確測量[2-3]。因此，研究轉動部件特別是多轉動單元、多自由度耦合角動量輸出的測量方法具有較大工程意義[4]。

1 測量原理

轉動部件對其安裝面的力學輸出可以用力矩和角動量2個參數表示，這2個參數分別表示力學作用的瞬時效應和累積效應，兩者可以通過微分或積分運算相互轉換。測量和評估轉動部件對其安裝面的力學輸出特性，可以通過測量輸出力矩或輸出角動量實現。但是，直接對輸出力矩進行測試，系統需要較高的帶寬，因此試驗中往往對輸出角動量進行測量，如果需要了解瞬時作用情況，則對輸出角動量進行微分運算即可。

角動量計算公式為

式中：J——轉動慣量；

ω——角速度。

由式（1）可知，具有單個轉動單元的轉動部件的角動量輸出，可以通過測量轉動單元的轉動慣量和轉動單元相對安裝面的角速度實現。但是，對于多轉動單元、多自由度以非正交方式耦合的情況，如果分別對各個轉動單元角動量輸出進行測量，然后通過耦合分析得到的綜合輸出會因中間環節過多而增大測試誤差。利用氣浮平臺可以實現轉動部件耦合角動量輸出的直接測量，從而減少中間環節，提高測量精度。

氣浮臺充氣狀態下，摩擦力矩很小。忽略氣浮臺摩擦力時，氣浮臺轉動臺面所受外力矩為零，氣浮臺旋轉臺面及臺面負載（主要有被測轉動部件、其他測量設備等）組成的系統角動量守恒。因此，氣浮平臺作為一個動量守恒系統，可以模擬空間衛星平臺。設氣浮臺轉軸為z軸，則有

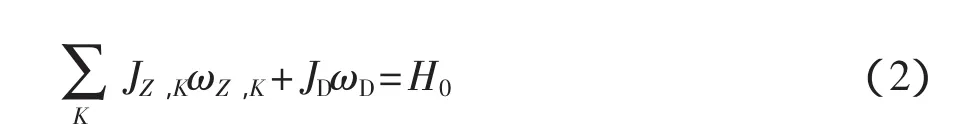
式中：JZ，K、ωZ，K——被測轉動部件的第K個轉動單元繞z軸的轉動慣量及轉速沿z軸的分量；

JD、ωD——系統定子（包括氣浮臺轉動臺面和相對臺面靜止的臺面負載）繞z軸的總轉動慣量及角速度；

H0——系統的初始角動量沿z軸的分量。

若系統初始角動量為零，則式（2）簡化為

試驗關心的是轉動部件工作時對其安裝面輸出角動量的大小，不是其自身角動量的大小。因此，對式（3）整理可得被測轉動部件輸出角動量Hout為

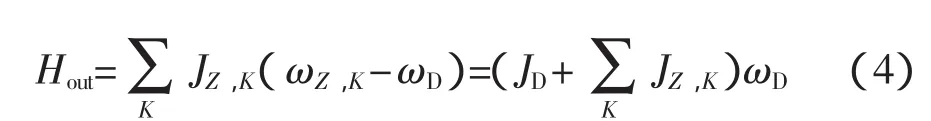
——轉動部件力學輸出對系統的擾動，對其進行微分，即可得到轉動部件輸出力矩的大小及變化情況。

對于系統初始轉動慣量不為零的情況，式（4）變為

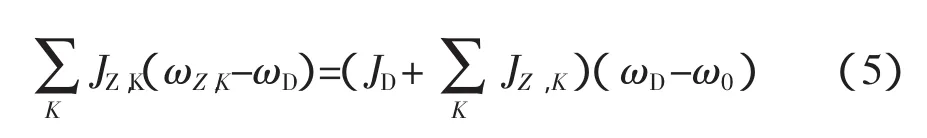
式中：ω0——系統初始角速度。

2 測量裝置與方法

2.1 測量裝置

測試平臺選用摩擦力矩小于0.001N·m單軸氣浮平臺,在其轉軸自由度上角動量近似守恒。整個測試系統如圖1所示。

圖1 角動量測試系統構成示意圖

整個測試系統由單軸氣浮平臺、高精度砝碼、光纖速率陀螺及數據采集系統、時統、無線通信模塊以及數據處理計算機等構成。測試系統工作原理如圖2所示。

圖2 角動量輸出測量原理框圖

2.2 測量方法

測試分為2步：（1）測量氣浮平臺轉動臺面及臺面負載的轉動慣量；（2）測量轉動部件工作時氣浮臺轉動角速度。

基于氣浮平臺的轉動慣量測量方法有如下3種：落體法[5]、附加轉動慣量法[6]、附加慣量扭擺法[7-8]。

重點介紹落體法（加速度法）：在氣浮平臺轉動臺面外沿上纏繞一條柔軟而不易變形的細線（吊線），吊線的一端固定在氣浮平臺的外沿上，另一端通過滑輪固定在落體上，如圖1所示。氣浮臺承受落體重力矩的作用，作勻加速運動，測量落體質量及氣浮臺轉動的角加速度，按式（6）計算轉動慣量。

式中：m——落體質量，kg；

R——氣浮臺轉動臺面半徑，m；

ω˙——氣浮臺轉動角加速度，rad/s2；

M0——氣浮臺摩擦力矩，N·m。

若氣浮臺摩擦力矩可以忽略，從式（6）可知，只要對落體質量及氣浮臺轉動角加速度進行精確測量，即可實現任意復雜不規則物體轉動慣量的測量。

在氣浮臺摩擦力矩不能忽略的情況下，為消除摩擦力矩的影響，可采用差值落體法，即先后懸掛2個質量不同的落體分別進行測量。

摩擦力矩可以認為與落體質量無關，則改變落體求得轉動慣量為

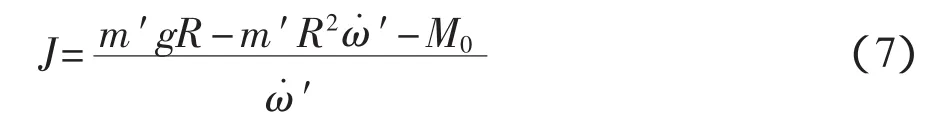
將式（6）和式（7）對比，消去 M0得到通過 2次吊掛落體測量轉動慣量的計算式為

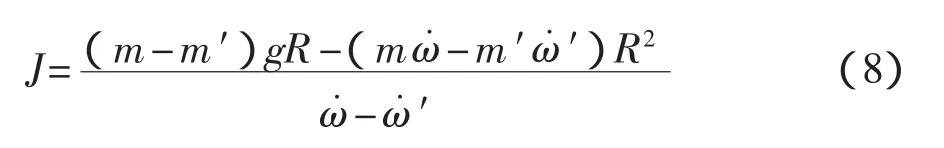
利用速率陀螺分別測量氣浮平臺初始角速度和被測轉動部件工作時氣浮平臺的角速度，然后計算被測轉動部件輸出角動量。

3 試驗及結果分析

3.1 測量精度驗證試驗

為驗證該系統的測量精度，以質量為50.30kg、轉動慣量為1.096kg·m2標準體為例進行了試驗。

（1）使氣浮臺浮起并進行調平，將被測轉動部件固定在氣浮臺轉動臺面上，并使其與氣浮臺同軸。

（2）測量氣浮臺轉動臺面及臺面裝置的轉動慣量，測試采用落體法。具體試驗方法：在臺面直徑為D=1m的氣浮臺邊緣處通過滑輪懸掛質量為m=500g的標準砝碼。速率陀螺測量氣浮臺轉動角速度，其曲線如圖3所示。用Matlab軟件對氣浮臺轉動角速度進行擬合，得氣浮臺轉動角速度表達式為

ω=8.985t-2.9913

則氣浮臺的角加速度為

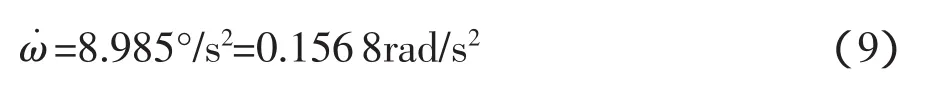
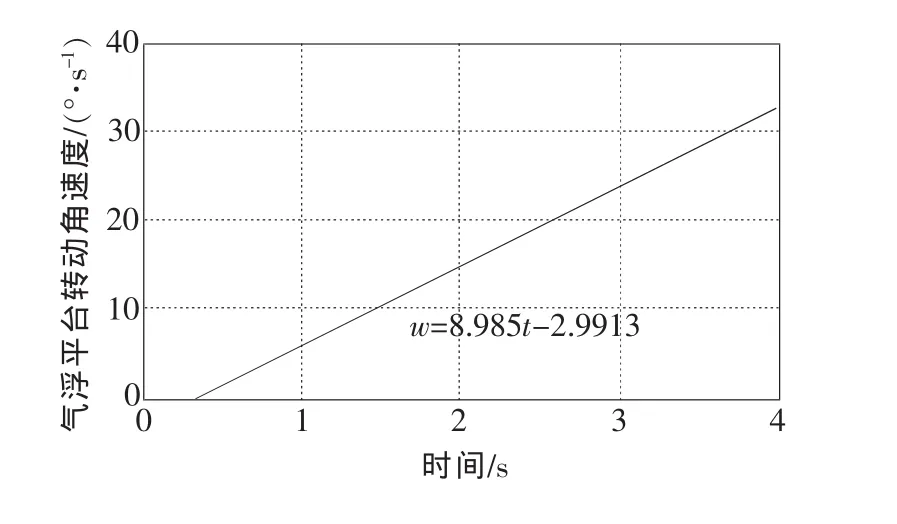
圖3 氣浮平臺轉動角速度曲線

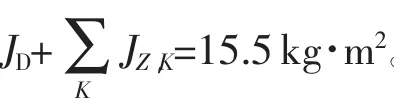
（3）利用速率陀螺測量氣浮臺初始角速度。由于氣浮臺難以絕對調平而且其摩擦力矩極小，其初始速度呈正弦振動，且阻尼很小。其角速度曲線如圖4所示。

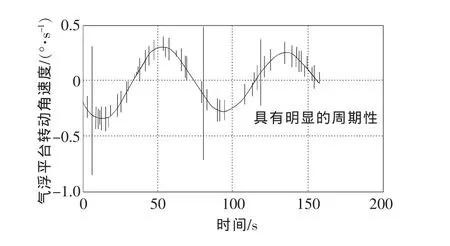
圖4 氣浮臺初始角速度曲線

（4）驅動被測轉動部件做速度為 ω=8sin（0.5 t）的正弦轉動，此時，氣浮臺角速度曲線如圖5所示。

圖5 氣浮臺轉動角速度曲線

3.2 數據處理與分析

為了消除氣浮臺初始角速度對測量結果的影響，對氣浮臺初始角速度（圖4）及轉動部件工作時氣浮臺角速度（圖5）進行頻譜分析得到：圖5曲線的2個峰值頻率為0.0122Hz和0.07935Hz，分別與圖4曲線的峰值頻率和被測轉動部件的驅動頻率一致。根據該特性在測試結果中減去氣浮臺初始角速度的影響，處理后的角速度曲線如圖6所示。

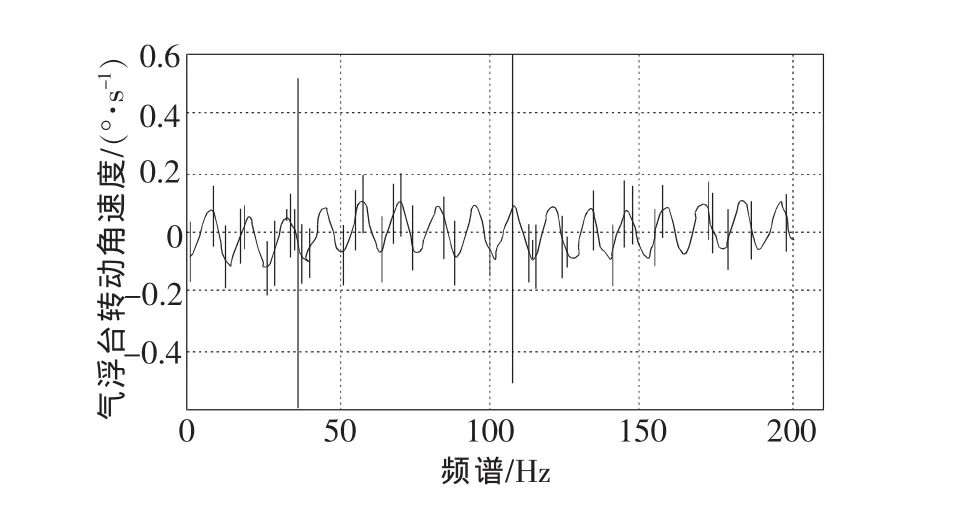
圖6 氣浮臺轉動角速度曲線

從上面的處理結果可以看出氣浮臺響應與被測轉動部件的運動同頻，為便于分析忽略時間延遲，得氣浮臺轉動角速度為

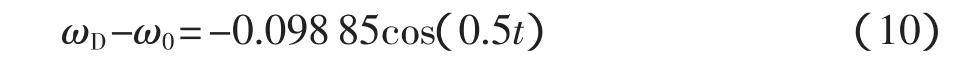
由式（5）可得被測轉動部件的角動量輸出為0.0268cos（0.5t），最大輸出角動量為 0.0268N·m·s。

3.3 測量誤差分析

由于轉動慣量和角速度的測試是獨立的，根據誤差傳遞的線性疊加法，則對測試結果進行誤差估算。測量誤差ΔH為

角速度測量由高精度光纖陀螺實現，陀螺測試精度可控制在0.003°/s以內。因此，取角速度測量誤差ΔωD、Δω0為 0.003°/s。轉動慣量測試誤差ΔJ受砝碼的質量、角加速度及氣浮臺轉動臺面直徑測量精度的影響。取砝碼質量誤差Δm=0.2g，氣浮臺轉動角加速度誤差 Δω˙=0.1°/s2，氣浮臺臺面直徑誤差 ΔR=1mm，計算得到轉動慣量測試誤差 ΔJ=0.0924kg·m2，由式（11）得測量誤差 ΔH=±0.00116N·m·s，相對測量誤差為4.3%。

4 結束語

采用單軸氣浮臺對復雜轉動部件，特別是對多運動單元多自由度運動的耦合角動量輸出進行測量，是研究轉動機構力學特性的一項重要手段。該方法的優點是可對耦合效果進行直接測量，不受具體耦合方式的限制，且測量精度較高，測試設備簡單，具有較強的工程應用價值。

[1]魯興舉.空間飛行器姿態控制仿真試驗平臺系統研究與設計[D].長沙：國防科技大學，2005.

[2]韓邦成.單軸飛輪儲能/姿態控制系統的仿真及其試驗研究[D].長春：中國科學院長春光學精密機械與物理研究所，2004.

[3] 趙萬良.高精度高穩定度反作用飛輪設計與實現[D].上海：上海交通大學，2008.

[4] 鄧以高，田軍挺.飛行器姿態控制方法綜述[J].戰術導彈控制技術，2006，53（2）：7-13.

[5] 于治會.落體法測定構件慣性矩的幾個問題[J].上海航天，2000（2）：57-62.

[6] 李季蘇，吳振嵩.測試單軸氣浮臺轉動慣量的一種方法[J].航天控制，1994（3）：60-73.

[7] 楊輝，洪嘉振，余征躍.測量單軸氣浮臺轉動慣量的新方法[J].振動與沖擊，2001，20（2）：32-34.

[8] 賈杰，周鳳岐，周軍.三軸氣浮臺轉動慣量測試方法研究[J].航天控制，2006，24（2）：73-77.