二甲醚發動機PCCI-DI燃燒的數值模擬(Ι)

李 維，王 穩，黃勇成，汪 映

(1.西京學院 汽車學院，陜西 西安710123;2.西安交通大學 能動學院，陜西 西安710049)

采用均質充量壓縮燃燒(HCCI)方式可使發動機在中低負荷具有高的熱效率和低的PM和NOx排放，但HCCI還未從根本上解決著火時刻和燃燒速度的控制問題，因此HCCI燃燒技術目前只局限在內燃機的中低負荷范圍內應用［1］。采用在同一循環中使用預混進氣和缸內直噴的復合燃燒(PCCIDI)方式可縮短滯燃期、減少擴散燃燒部分的油量、降低最高燃燒溫度與壓力［2］。采用PCCI-DI燃燒方式不但可進一步提高二甲醚發動機的熱效率和降低NOx排放，而且發動機仍可在較寬廣的轉速和負荷下運行［3］。

目前，對二甲醚噴霧特性已經有了一些較深入的研究［4-5］。但利用二甲醚發動機缸內燃燒過程的數值模擬來闡述二甲醚發動機性能的研究還不是很多。由二甲醚與柴油的理化性質差異較大，因此直接使用原來適用于柴油燃料的壓燃式發動機過程的數值模擬并不完全適合用來研究二甲醚在發動機缸內的燃燒，但二者作為壓縮燃燒的燃燒過程還有著許多相似之處，可以在原有方法的基礎上進行一些改造來研究二甲醚的燃燒過程。為此，筆者采用數值模擬的方法開展PCCI-DI二甲醚發動機燃燒過程的研究。

為了對空氣運動、噴油特性和燃燒室幾何形狀等因素之間的配合進行數學分析和模型，以達到其最佳匹配實現高效低污染燃燒，要應用多維模型［4］。KIVA-Ⅲ是專門為模擬內燃機工作過程而設計的軟件，筆者以KIVA-Ⅲ程序基礎上，通過擴展和修改其中的噴霧、燃燒等模型來進行二甲醚發動機PCCI-DI燃燒過程的三維數值模擬。

數值模擬過程中，氣相模型由缸內氣體流動的守恒偏微分方程組、湍流模型方程和狀態方程等控制方程構成。湍流模型采用標準的κ-ε雙方程模型。本文僅就噴霧、燃燒模型做一介紹。

1 噴霧模型

1.1 噴霧方程

一般對噴霧的描述是采用概率統計的方法，液滴概率分布函數f定義如下:

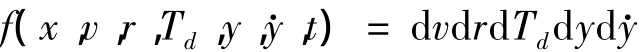
表示在t時刻位置x上，單位體積內，具有速度處于(v，v+dv)范圍內，半徑處于(r，r+dr)范圍內，溫度處于(Td，Td+dTd)范圍內，球形偏移參數處于(y，y+dy)和范圍內的液滴的概率意義上的個數。

液滴概率分布函數f的控制方程為:

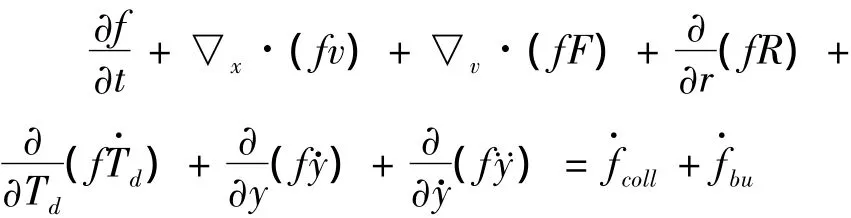
式中:t是時間;v為速度;r為液滴尺寸;F=dv/dt為液滴加速度;R=dr/dt為液滴尺寸r隨時間變化的速率;Td表示液滴溫度;y表示液滴圓球度和分別為由于液滴的碰撞和破碎而產生的源項。

但液滴概率分布函數的變量非常多，直接求解其控制方程幾乎不可能。筆者采用隨機質點方法，用離散的液滴來描述噴霧，并借助于蒙特卡洛方法，用一定數量的顆粒代表整群顆粒的采樣，每一個用于計算的顆粒被認為代表一群具有相同特征的顆粒。于是，連續分布的液滴概率分布函數可離散為:

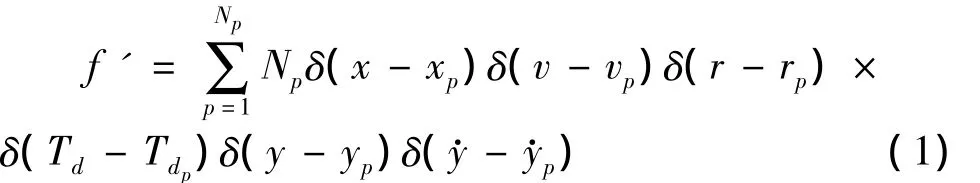
每一個顆粒p由Np個具有相同的位置xp、速度vp、直徑rp、溫度Td、振蕩參數yp和y·p的液滴組成。這些液滴運動軌跡相同，它們在空間中的運動受以下動力方程控制:

液滴的加速度F由氣相阻力和重力決定:

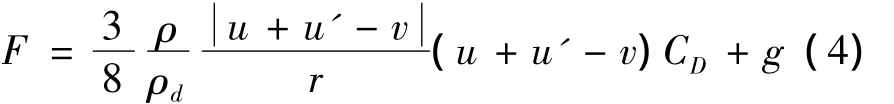
式中:u為氣相速度;u'為氣相湍流速度;v為噴霧粒子速度;ρd為液滴密度;阻力系數CD是根據小球在空氣中運動的Stokes關系，并結合實驗的修正而得到:

μair()可由式(6))求得:

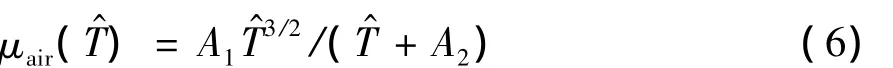
式中:A1和A2為常數。

1.2 液滴破碎模型

KIVA程序中采用的TAB(Taylor Analogy Breakup)液滴破碎模型是Taylor將液滴振動及變形與彈性質量系統比擬的基礎上得到的。對黏度甚小的二甲醚而言，其噴霧貫穿度小于柴油，噴霧錐角比柴油大［4-5］。因此，TAB模型對黏度甚小的二甲醚不易得到準確的結果。筆者采用Kelvin-Helmholtz(KH)Wave模型來進行計算［6］。

假設在液滴表面施加一個極小的偏移量，即

式中:η'0是擾動的初始振幅;?是波動的增長速率;k為波數;R表示為括號內復數函數的實數部分。列出連續方程和運動方程，并進行求解，可得到波動增長速率和波長的方程。其中波動的最大增長率Ω和相對應的波長Λ與氣液兩相物理特性的關系如下:

式中:We2=ρ2U2a/σ，是氣體的Weber數;We1=ρ1U2a/σ ，是液體的 Weber 數;Z=We0.51/Re1，是Ohnesorge數［Re1=Ua/v，是液體的Reynold數(U為液氣相對速度;a為液滴的半徑)］;T=ZWe0.52。

新生成的液滴半徑為:

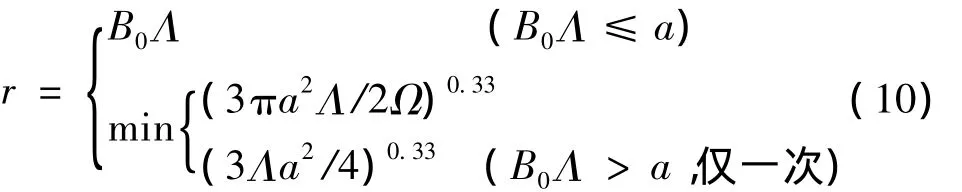
式中:B0=0.61。

原液滴半徑的變化遵從以下關系:

式中:τ為破碎時間，由式(12)計算:

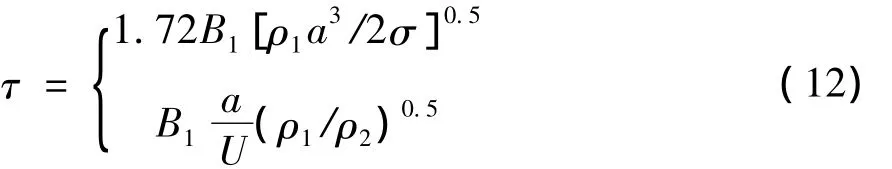
式中:B1為可調模型常數。

當液滴每次破碎后，子液滴具有與父液滴相同的溫度和位置，速度矢量在父液滴速度方向上的分量u為父液滴的速度U，在其垂直平面上2個速度分量分別為cosφ，θ為噴霧錐角，φ 按統計規律在(0，2π)隨機選取。

1.3 液滴蒸發模型

假定液滴是球對稱的，液滴內部溫度均勻，則根據液滴與周圍工質之間的能量平衡可得液滴溫度Td隨時間t的變化率方程:

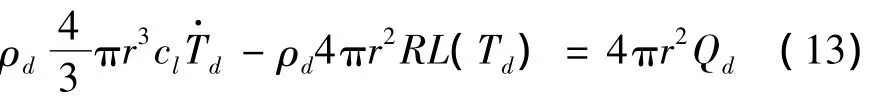
式中:L(Td)為液滴汽化潛熱;cl為液體的比熱;Qd為液滴表面單位面積上的導熱率。

液滴半徑變化率R由Frossling關系式給出:

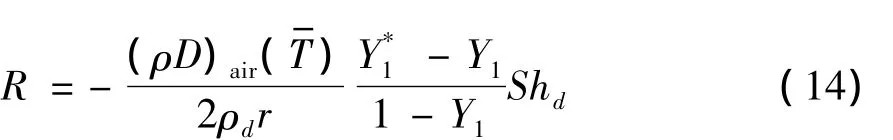
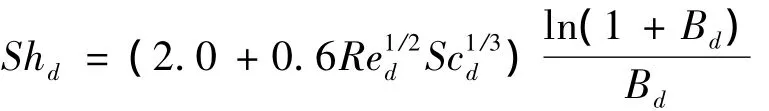
液滴表面燃油蒸氣的質量百分比Y*1的表達式為:

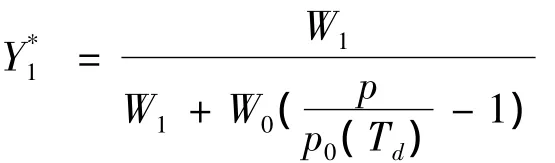
式中:W1為燃油蒸氣的分子量;W0為除燃油蒸氣外所有其它物質的局部平均分子量;p為工質總壓力;p0(Td)為在溫度Td下燃油蒸氣的分壓。

液滴表面單位面積上導熱率Qd表達式可由Ranz-Marshall關系式給出:

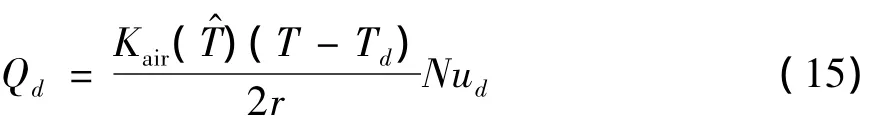
通過隱式迭代求解式(14)可以得到液滴溫度Td和尺寸r。

通過將t時刻處于位置x的所有液滴的質量、動量、和能量的變化率分別相加，就可以得到氣相控制方程中由于噴霧引起的的源項

由于DME的沸點甚低，密度又小，試驗中噴嘴啟噴壓力在16.0 MPa，同時噴霧是噴在高溫的燃氣當中［2］，二甲醚的噴霧貫穿度減小，因此，不存在燃油碰壁現象，所以噴霧模型中不考慮噴霧碰壁的影響。

2 燃燒模型

燃燒過程的模擬是建立在包括45個組分的351個反應的反應機理之上［5-6］，可將這一機理編入KIVA程序代碼中用于DME模擬計算。但KIVA程序中所采用的湍流混合控制燃燒模型難以使用詳細的化學反應機理，因此筆者采用部分攪拌反應器(Partially Stirred Reactor，PaSR)燃燒模型。

2.1 質量守恒方程

系統內發生的化學反應可表達為:

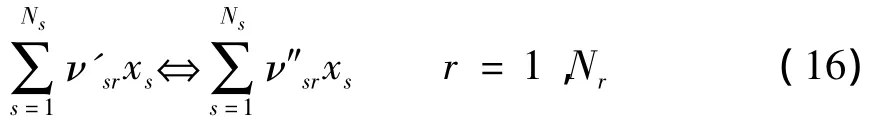
式中:xs代表1 摩爾的組分s;ν'sr，ν″sr分別為正、逆反應的化學計量系數;Ns為參與反應組分的數量;Nr為發生化學反應的數量。

在連續方程中化學反應的源項可以表示為:

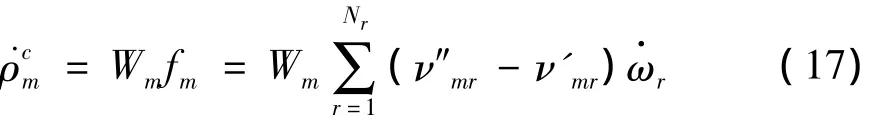
化學反應速率由式(18)給出:

式中:fm為組分m的摩爾濃度變化率;cs=ρs/Ws為第s種組分的摩爾濃度(其中ρs，和Ws分別為組分s的密度和分子量);分別為正向和逆向的反應

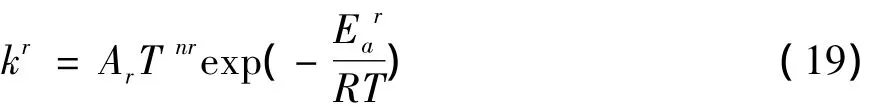
式中:nr，Ar和Era分別為與空間因子、碰撞頻率和活化能相關的經驗參數。

2.2 參考組分方法

由于采用詳細的化學反應機理模擬燃燒，而不同的化學反應的特征時間相差很大，因此化學反應源項的計算是剛性的(即強烈依賴于時間)。為此必須解決計算時間步長選取這一問題，于是引入了參考組分方法。

考慮下面基元反應

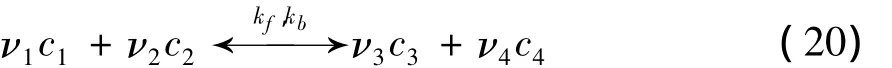
式中:νi，ci分別為反應計量系數和摩爾濃度。由于大多基元反應的計量系數不大于2，為了簡化，令νi=1。于是上述基元反應的速率為:

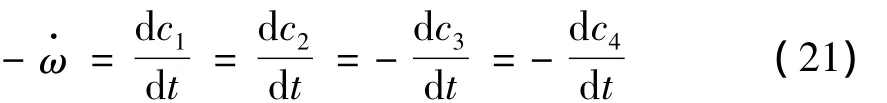
速度常數，其表達式為修正的阿累尼烏斯形式:

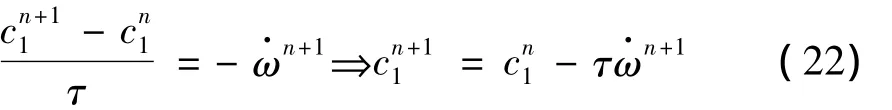
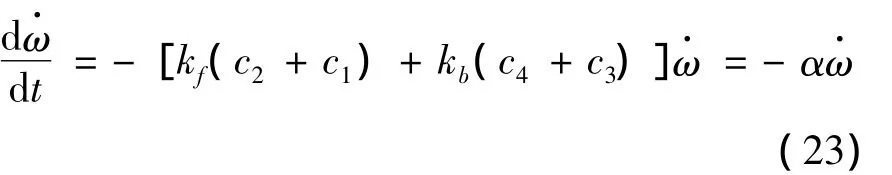
式中:α=kf(c2+c1)+kb(c4+c3)。采用半隱式格式離散式(23)得:

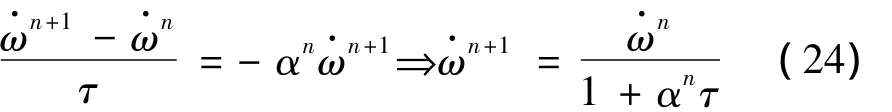
將式(24)代入式(22)得到:

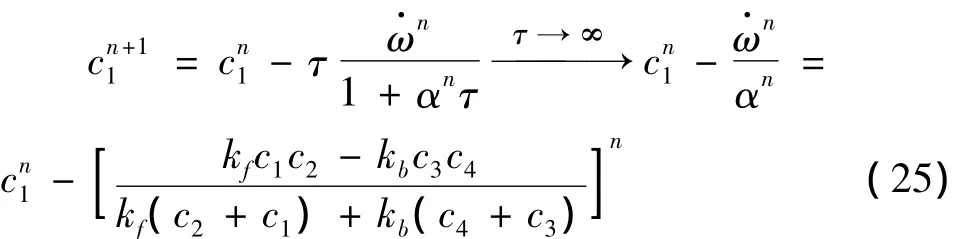
為了解決這個問題，引入參考組分方法。其中，參考組分定義為在化學反應中其濃度變為負數的危險性最大的組分，參考組分被化學反應所消耗，且具有最低的濃度。為了便于討論，假定參考組分cr為c1，則c2＞＞c1，于是有:

將式(26)代入式(25)得:

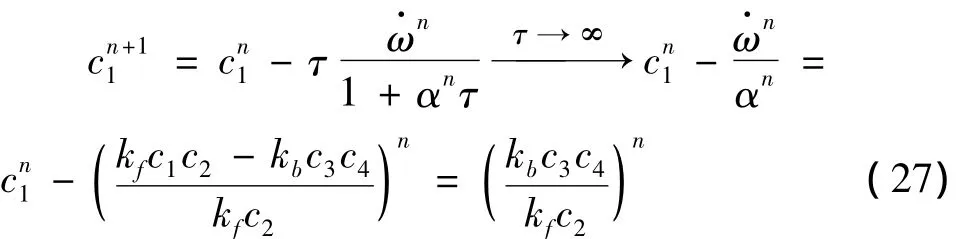
采用參考組分方法后，對于每個化學反應自動滿足化學平衡條件，不必將反應速度很快的平衡反應和反應速度較慢的動力反應分開來處理，消除了化學反應中組分濃度變為負數的危險性，而且還給出了化學反應的特征時間尺度τchem為:

雖然根據式(24)、式(28)可以求得化學反應產生的源項，但沒有考慮湍流的影響。為了同時考慮化學反應和湍流對燃燒的影響，可引入部分攪拌反應器燃燒模型。

部分攪拌反應器(Partially Stirred Reactor，PaSR)燃燒模型是Golovitchev等人在渦耗散概念(Eddy-Dissipation Concept，EDC)燃燒模型的基礎上發展而來，而且在EDC燃燒模型中結合使用詳細的化學反應機理，自燃和燃燒的建模便沒有了本質的區別，因此沒有必要對自燃過程再建立模型［7］。

在PaSR模型中，每個計算單元被分成反應區和非反應區，如圖1。

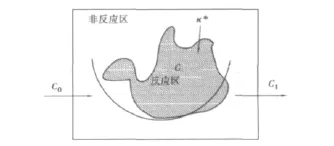
圖1 PaSR反應器示意Fig.1 Schematic diagram of PaSR Reactor

反應區視為完全攪拌反應器(Perfectly Stirred Reactor，PSR)，占整個計算單元的體積分數為k*。為了便于分析，反應器中定義了以下3個平均濃度:進口處組分平均濃度c0，反應區組分濃度c和反應器出口處組分濃度c1。在一個時間步長τ內，計算過程可按以下2步進行:第1步，化學反應使反應區中組分濃度從初始的c0變化到c;第2步，在湍流作用下反應區(組分濃度為c)與未反應區(組分濃度為c0)混合使組分平均濃度變為c1，第2步經歷的時間為τmix。于是經歷一個時間步長τ后，計算單元中組分平均濃度為:

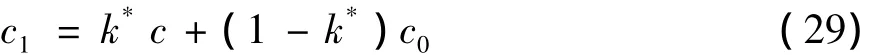
式(29)中次網格中反應區濃度c為未知量，必須用單元中已知信息來表達。為此假定在計算步長τ內計算單元中組分濃度從c0變化到c1的平均速率與在混合時間τmix內反應區組分濃度從c變化到c1的平均速率相等，并與式(17)表達的化學反應的源項相對應，于是有:

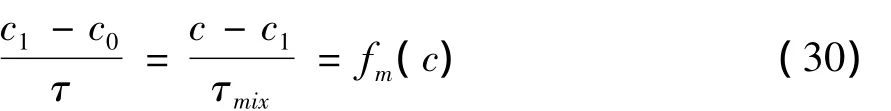
由式(29)和式(30)可得:

式(30)表明計算時間步長大于混合時間，當k*趨近于1時整個計算單元為反應區，而當k*趨近于0時，整個計算單元沒有發生化學反應。確定了反應區體積分數k*后，需消除未知量c以求得c1。

fm(c)在c1附近的Taylor展開式為:

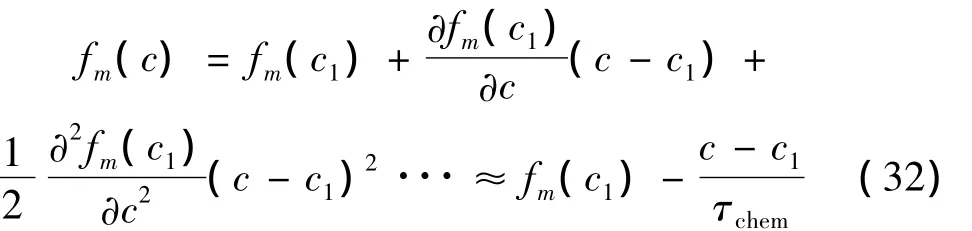
由式(29)得到c的表達式后代入式(32)并結合式(30)得:

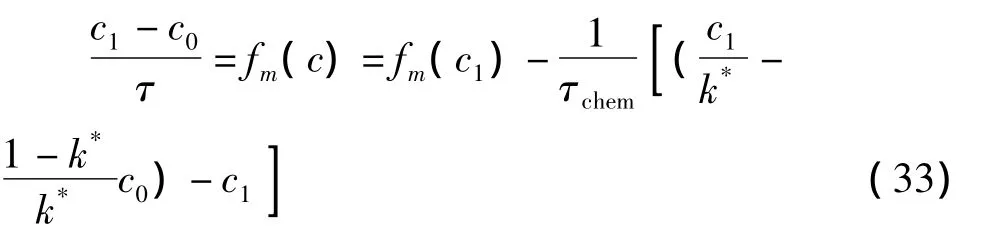
由式(33)可得到PaSR模型中計算化學反應源項的方程

2.2.1 湍流混合時間 τmix的確定

τmix表征的是PaSR反應器中新鮮、未發生反應的混合物與已燃氣體間混合過程的特征時間。對于考慮湍流與化學反應相互作用的燃燒模型，正確選擇微混合時間至關重要。從較大的漩渦到分子水平，表征湍流時間尺度的參數有許多。Kj?ldman對Kolmogorov尺度，Taylor尺度以及 Kolmogorov和Taylor尺度的幾何平均等3種時間尺度進行了研究，發現采用Taylor時間尺度結果最佳。本文也采用Taylor時間尺度計算微混合時間。對于κ-ε湍流模型有:

式中:Cmix為模型常數。

2.2.2 化學反應特征時間尺度τchem的確定

化學反應時間尺度有多種定義方式。本文中化學反應時間尺度的定義基于參考組分cr參與反應的時間(參考組分具有最短的壽命)，即:

由式(16)可得:

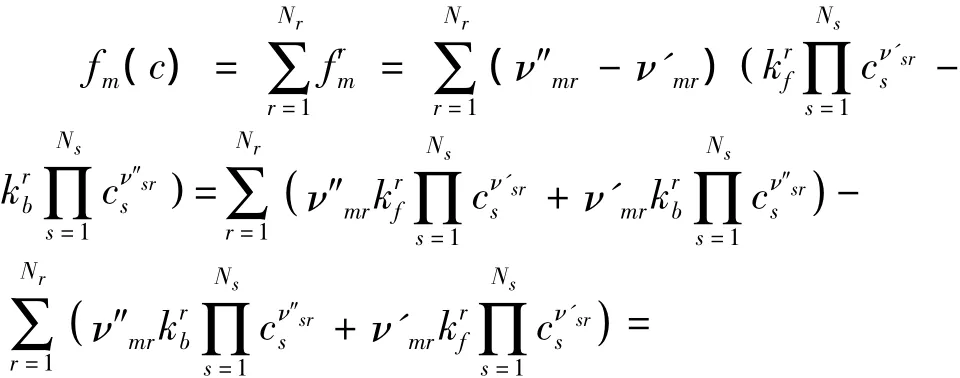
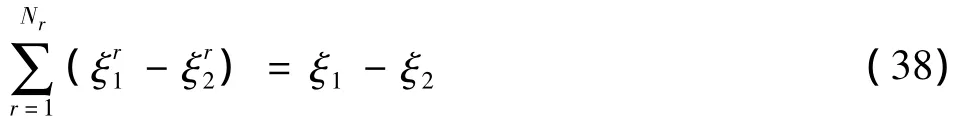
對于第r個反應，其反應速率為:

由于反應速率是一個與所有組分濃度相關的高度非線性函數，為了簡化計算，利用前面介紹的計算反應速率的參考組分法，在參考組分cr附近對式(35)線性化后有:

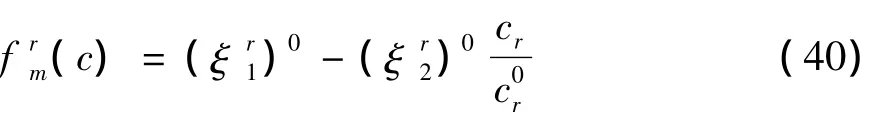
式中:上標0表示計算初始值，為已知量。對式(40)求導得:

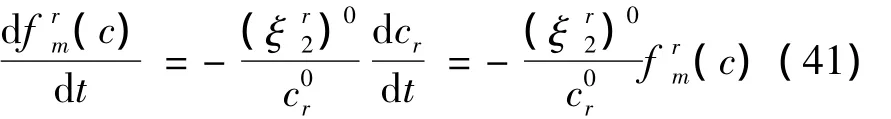
為了獲得下一步長的反應速率，采用半隱式格式離散式(41)可得［8-9］:

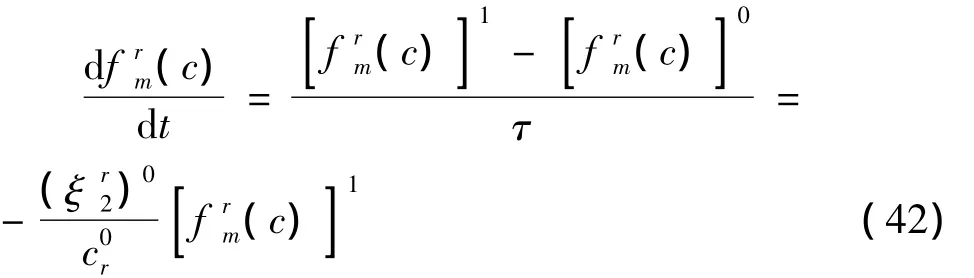
其中:上標1表示下一步長的值。于是可以得到下一步長的反應速率和反應時間尺度:

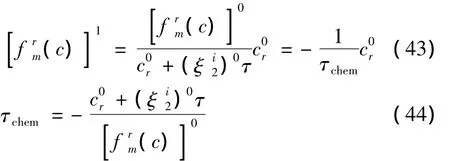
將第r個反應的反應速率即式(43)，代入PaSR方程［即式(34)］可得:

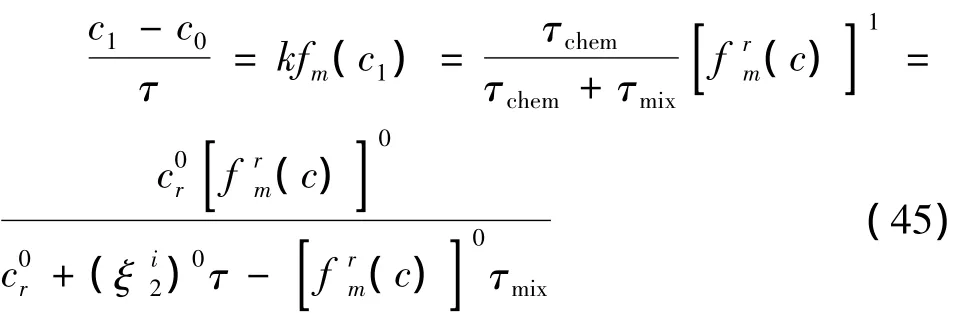
3 邊界條件

一般固體壁面附近的邊界層很薄，用實際計算網格難以求解，在湍流流場中，邊界可采用湍流壁面函數代替。

油膜的蒸發使氣相產生了垂直于壁面的速度，因而改變了壁面油膜上方的湍流邊界層。定性地講，有蒸發的湍流邊界層相對于無蒸發的邊界層對質量、動量、能量的輸運有抑制作用。因此，必需建立一個適用于油膜蒸發的壁面函數才能較精確地描述邊界層上質量、動量、能量的輸運。

推導壁面函數的過程中，作了以下2點假設:

①整個輸運是湍流擴散和蒸發所引起的對流輸運的總和，且與壁面法向坐標無關;②象無蒸發邊界層那樣，假設湍流擴散率與壁面距離成正比。

［y+=(νl為層流動力黏性);K為湍動能;cμ=0.09;Scl，ScT分別為層流和湍流的Schmidt數;κ =0.433，為 Karmann 常數］;Yv為在y+處燃油蒸汽質量百分比;Yv0為在溫度為Ts下飽和燃油蒸汽質量百分比。

壁面剪切應力方程為:

邊界層熱流量方程為:

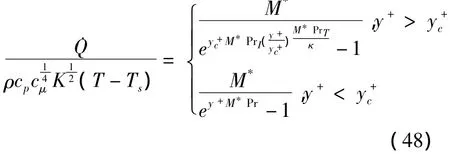
式中:Prl，PrT分別為層流和湍流Prandtl數。邊界層速度方程為:

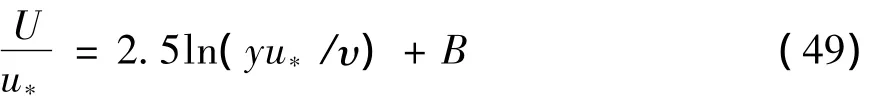
其中:U為距壁面y處的流速切向分量;υ為分子運動黏度;B為壁面粗糙度常量;u*為剪切速度。

在計算湍流流動時，湍動能κ和湍流耗散率ε按距壁面距離為y處計算，邊界條件為:

4 結語

1)針對二甲醚噴霧貫穿度小，噴霧錐角大的特點，可采用WAVE破碎模型替代KIVA程序中的TAB模型;

2)采用部分攪拌反應器(Partially Stirred Reactor，PaSR)燃燒模型替代程序中所用的湍流混合控制燃燒模型可以使用詳細的化學反應機理并將其編入KIVA程序中用于DME模擬計算。

［1］朱馳，劉圣華.二甲醚均質充量壓燃發動機排放特性的試驗研究［J］.內燃機學報，2004，22(1):51-54.ZHU Chi，LIU Shen-hua.Experiment investigation of DME HCCI engineemissions［J］. Transactions ofCSICE，2004，22(1):51-54.

［2］李維，周龍保，汪映，等.DME部分預混壓燃與缸內直噴復合燃燒的研究［J］.重慶交通大學學報:自然科學版，2010，29(3):480-483.LI Wei，ZHOU Long-bao，WANG Ying，et al.Experimental investigation on combustion characteristics of partial premixed charge compression ignition–direct injection engine fueled with dimethyl ether［J］.Journal of Chongqing Jiaotong University:Natural Science，2010，29(3):480-483.

［3］李維，汪映.DME預混合引導進氣實現PCCI-DI燃燒的試驗研究［J］.車用發動機，2008，177(4):15-18.LI Wei，WANG Ying.Experimental investigation on the realization of PCCI-DI combustion by DME pilot from the intake pipe［J］.Vehicle Engine，2008，177(4):15-18.

［4］王賀武，周龍保.二甲醚噴霧特性的研究［J］.西安交通大學學報:自然科學版，2001，35(9):1480-1483.WANG He-wu，ZHOU Long-bao.Study on spray characteristics of dimethyl ether［J］.Journal of Xian Jiaotong University:Natural Science，2001，35(9):1480-1483.

［5］馬愛兵，劉建江.對二甲醚的噴霧特性研究［J］.新技術新工藝，2008，11(4):99-100.MA Ai-bing，LIU Jian-jiang. Study on the characteristics of Dimethyl Ether(DME)general spary［J］.New Technology ＆New Process，2008，11(4):99-100.

［6］蔣德明.內燃機燃燒與排放學［M］.西安:西安交通大學出版社，2001:479-500.

［7］Golovitchev V I，Nordin N，Jarnicki R ，et al.3-D Diesel Spray Simulations Using a New Detailed Chemistry Turbulent Combustion Model［EB/OL］.［2000-01-1891］.http://papers.sae.org/2000-01-1891.

［8］Fischer S L，Dryer F L，Curran H J.The reaction kinetics of dimethyl ether I:High-temperature pyrolysis and oxidation in flow reactors［J］.International Journal of Chemical Kinetics，2000，32(10):714-740.

［9］Curran H J，Fischer S L，Dryer F L.The reaction kinetics of dimethyl etherII:Low-temperature oxida-tion in flow reactors［J］.International Journal of Chemical Kinetics，2000，32(10):741-759.