輸油管道土壓力分析

周正峰，凌建明，梁 斌

(1.西南交通大學 土木工程學院，四川 成都610031;2.西南交通大學高速鐵路線路工程教育部重點實驗室，四川成都610031;3.同濟大學道路與交通工程教育部重點實驗室，上海201804;4.中國航空油料有限責任公司，北京100088)

土壓力是埋地輸油管道承受的最主要恒荷載，同時，施工荷載或交通荷載對管道的影響，也是通過管周土體的傳遞并最終以土壓力形式作用在管道上，因此，土壓力計算是管道受力分析的基礎。幾十年來，國內外許多學者提出了多種管道土壓力計算模型，主要包括以下幾大類:①基于極限平衡理論的土柱滑動面模型(如 Marston 模型［1］、曾國熙模型［2］等);②從變形條件出發的彈性地基梁模型(如顧安全模型［3］、折學森模型［4-5］等);③經驗土壓力集中系數模型［6］;④土柱法［7］。這些土壓力計算方法主要是針對剛性管道，即假定在土壓力作用下管道斷面的變形量很小，計算時可以忽略不計，管道受到的水平向土壓力采用朗肯主動或被動土壓力公式進行計算。

然而，埋設于地基中的輸油管道為薄壁鋼管，在豎向荷載作用下，變形的薄壁鋼管使土體位移產生彈性抗力，這抗力的發生與發展又反過來對管壁的進一步繼續變形起約束與抑制作用，與此同時，管周土壓力集度發生重分布，并趨向均勻化。薄壁鋼管管土之間的相互作用對土壓力的分布和大小有顯著影響，采用針對剛性管的土壓力計算方法不再適用，R.C .Prevost，等［8］強調了考慮管土相互作用對薄壁鋼管這類柔性管計算分析的重要性。

筆者應用大型通用有限元軟件ABAQUS，建立考慮管土相互作用的輸油管道有限元模型。應用該模型，分析管周土壓力的分布、大小和管土相對剛度，并與現有理論公式計算結果進行對比，說明管土相互作用對管周土壓力和管土相對剛度的影響。

1 管道有限元模型

1.1 結構和材料參數

以管徑D為610 mm、壁厚δ為10.3 mm的輸油管道為例。管材模量Ep為2.05×105MPa，泊松比μp為0.3，不考慮管道自重;管頂埋深H假定為3D(1.83 m);回填土容重 γ1取18 kN/m3，變形模量E1取8 MPa，泊松比 μ1取 0.35，內摩擦角 φ 為30°，不考慮土體黏聚力。模型采用線性平面應變單元CPE 4模擬管道和土體。

管道地基考慮軟基和硬基兩種情況，變形模量E0分別取8 MPa和80 MPa，泊松比 μ0均取0.35，由于地基呈自平衡狀態，故不計容重。管道地基采用弧形基床，基床包角假定為120°。通過收斂性分析，確定模型尺寸為兩側距管道中心3.5D、地基底部距管道中心4.5D。邊界條件為對稱面采用對稱邊界，側面約束水平位移，底面約束豎向位移。管道分析模型如圖1。

圖1 管道分析模型Fig.1 Pipe analysis model

1.2 管土相互作用模型

管土相互作用涉及到土體與管道2種不同介質間的接觸問題，合理模擬管土之間的接觸行為是研究埋地管道力學行為的重要前提。管土之間的接觸作用屬于復雜的邊界非線性問題，涉及管土接觸面的相對滑動和張開等接觸問題。筆者采用庫倫摩擦接觸模型來模擬管土接觸面上的法向和切向作用［9］。

管道與周圍土體之間摩擦系數的取值變異性較大，它與管道表面粗糙度、土壤類型、壓實度以及干濕狀況等因素有關，管土摩擦系數取 0.25［10］，同時，也考慮回填土與原地基土之間的摩擦，摩擦系數取0.577(tgφ)。

2 管周土壓力分布

整理計算結果，得到管周土壓力分布如圖2。

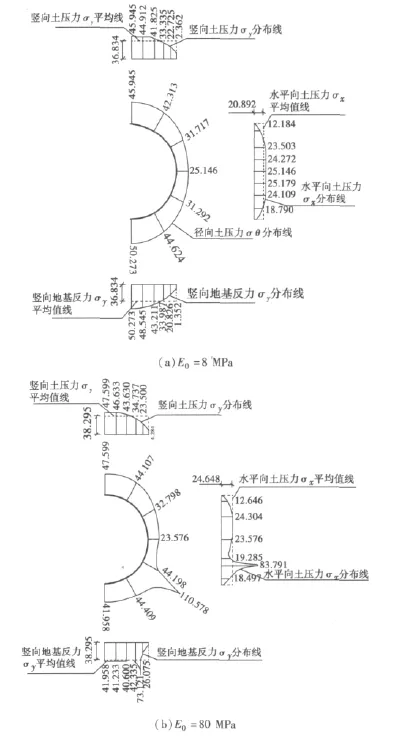
圖2 管周土壓力分布(單位:kPa)Fig.2 Earth pressure distribution around pipe

從圖2中可以看出:

1)對于管道地基強度與回填土相同的情況［圖2(a)］，徑向土壓力最大值出現在管底C點(50.273 kPa)，徑向土壓力最小值出現在管側B點(25.146 kPa);對于管道地基強度遠大于回填土的情況［圖2(b)］，徑向土壓力最小值出現在回填土區的最低點附近，徑向土壓力最大值出現在與之相鄰的管道地基一側，這是由于管道地基剛度遠遠大于回填土，根據剛度分配外荷載的原則，徑向土壓力在回填土與管道地基交界處發生突變。

2)管周環向剪應力分布如圖3，管周最大剪應力大致出現在管肩(45°)和管腰(135°)位置，隨著地基強度的增大，管道地基部分的管周剪應力有所減小。

圖3 管周剪應力分布(單位:kPa)Fig.3 Shear stress distribution around pipe

3)徑向土壓力和環向剪應力轉化為豎向土壓力和水平向土壓力之后，在管徑寬度或高度范圍內大致按拋物線分布，同樣在回填土與管道地基交界處因剛度差異而發生突變。Marston等土壓力理論假定豎向土壓力為沿水平直徑寬度均勻分布，水平向土壓力以朗肯主動土壓力表示，其大小隨深度按線性規律遞增，呈梯形分布。實際上，由于管殼下半圓(反拱)的邊界形狀將對填土水平向土壓力分布產生影響，水平向土壓力將隨深度增加而遞減，有限元分析結果更符合實際情況。

3 管周土壓力大小

以管道地基變形模量E0取8 MPa為例，對比分析有限元法、彈性理論解［11］、Marston土壓力理論［1］、曾國熙公式［2］、顧安全公式［3］和土壓力系數法［6］計算得到的管道土壓力系數，如表1。

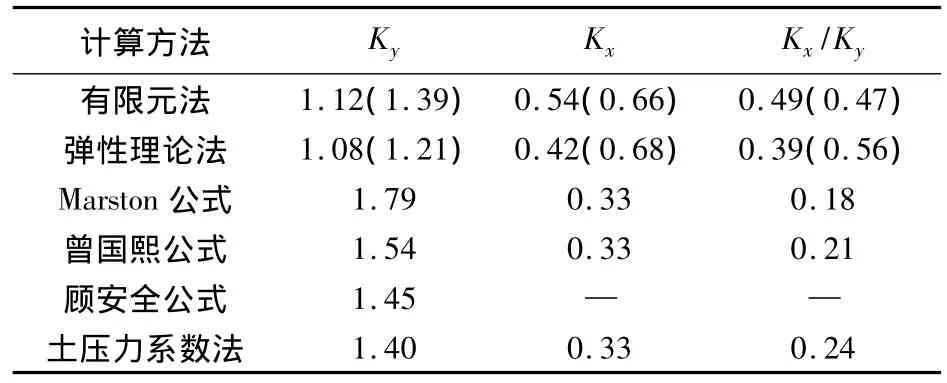
表1 土壓力系數Tab.1 Earth pressure coefficient

表中，豎向土壓力系數Ky為管道水平直徑寬度范圍內受到的平均(括弧內為最大)豎向壓力與地面至管頂土柱重量之比，水平向土壓力系數Kx為管道豎向直徑高度范圍內受到的平均水平壓力與地面至管道中心回填土重量之比。從表1中可以看出:

1)有限元法和彈性理論法得到豎向土壓力系數要小于Marston等理論公式的計算結果，而得到水平向土壓力系數要大于Marston等理論公式的計算結果。這主要是由于有限元法和彈性理論法能夠考慮管土之間的相互作用。由于管環發生橫向側移和土體對管環側移的約束，使得管周土壓力發生重分布，豎向土壓力減小，水平向土壓力增大。而Marston等理論公式將管道視為剛性管，忽略了管環的橫向側移。另外，Marston計算水平向土壓力采用朗肯主動土壓力，而實際上管環變形的趨勢總是擠壓管側土體，而不是與土體相脫離，管環側移方向與水平土壓力對管壁的作用方向總是相反，與朗肯主動土壓力導出的概念正好相反。因此，有限元法得到的土壓力分布形式和大小更符合實際情況。

2)管道受到的豎向土壓力總是大于水平向土壓力。比較水平向土壓力系數與豎向土壓力系數的比值可知，有限元法和彈性理論法得到的管周土壓力分布較Marston等理論公式計算結果更加均勻，較大的水平向土壓力將使在豎向荷載作用下已趨扁平的管環，部分地向正圓恢復，有利于降低管道結構應力和提高管道穩定性。Marston等理論公式低估了管道水平向土壓力，使得管道的不均勻受力狀態更加嚴重，再加上對管道豎向土壓力的計算偏大，將導致管道的水平徑向變形和截面內力計算結果偏大。

4 管土相對剛度

管土相對剛度指管道的自身剛度與管道周圍土體的剛度之比，不同剛度的管道在土壓力作用下的受力與變形機理不同。管土相對剛度根據管道截面剛度與管周土體剛度的比值來確定，并以管土相對剛度比λ來表示其大小［12］:

在現行理論計算方法中:

則:

式中:qv為均布豎向壓力;r為管道的平均半徑;t為管道的平均壁厚;Ep為管道的彈性模量;Ip為管道截面慣性距;E1為回填土的變形模量。

對于管徑D=610 mm、壁厚δ=10.3 mm的輸油管道，當回填土變形模量取8 MPa時，根據式(4)計算得到的管土相對剛度比λ=0.13，即管道屬于柔性管，管道受到的豎向土壓力應小于管頂土柱重力［12］，而有限元計算結果卻表明管頂豎向土壓力系數略大于1，即管道與土體的剛度相當。

分析管土相對剛度計算結果的差異:公式(4)在計算管道豎向變形時，采用的計算模型如圖4(a)所示。該模型將管道與管周土體完全隔離，僅僅考慮管頂均布豎向壓力的作用，忽略了管周土體彈性抗力的影響，并假設管底豎向反力沿管徑寬度范圍內均勻分布。而實際管道受力狀態大致如圖4(b)所示，管土之間的相互作用將使管道受力和變形產生重分布。因此，人為地將管道與管周土體完全分開，忽略管道與管側土體的相互作用，使得管道豎向變形計算結果比實際要大，導致管土相對剛度判定產生偏差。

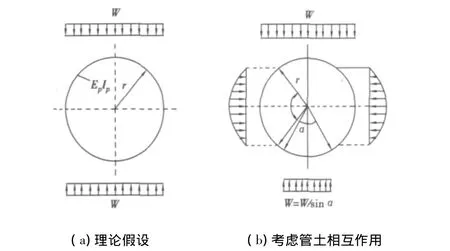
圖4 計算管土相對剛度時的管周土壓力分布Fig.4 Earth pressure distribution around pipe as pipe-soil relative stiffness determination

5 結論

1)應用ABAQUS通用有限元軟件，采用庫倫摩擦模型模擬管土接觸面上的法向和切向行為，建立了管土結構有限元分析模型。

2)揭示了管周土壓力的分布形態:徑向土壓力最大值出現在管底、最小值出現在管側，但當管座地基與回填土剛度不同時，在交界面處發生突變;切向土壓力最大值出現在管肩和管腰，最小值出現在管頂和管底。轉化成豎向和水平向土壓力，在管徑寬度和高度范圍內大致呈拋物線分布。

3)考慮管土相互作用得到的豎向土壓力系數要小于Marston等理論公式的計算結果，得到的水平向土壓力系數要大于Marston等理論公式的計算結果，而得到的管土相對剛度要遠大于現有理論公式的計算結果，在輸油管道力學分析時必須考慮管土之間的相互作用。

［1］Spangler M G.Underground Conduits:An Appraisal of Modern Research［C］.Washington，D.C.:Proceedings American Association of Civil Engineening，1948.

［2］曾國熙.土壩下涵管豎向土壓力的計算［J］.浙江大學學報，1960:5(1):79-97.ZENG Guo-xi.Calculation of vertical earth pressure on the conduit under Culvert［J］.Journal of Zhejiang University，1960:5(1):79-97.

［3］顧安全.上埋式管道及洞室垂直土壓力的研究［J］.巖土工程學報，1981，3(1):3-15.GU An-quan.Investigation of the vertical earth pressure on projecting conduit and underground chamber under a high embankment［J］.Chinese Journal of Geotechnical Engineering，1981，3(1):3-15.

［4］折學森，顧安全.高填土下管道土壓力的分析［J］.西安公路學院學報，1992，12(4):27-33.ZHE Xue-sen，GU An-quan.Study of the earth pressure on conduit under the deeper earth［J］.Journal of Xi’an University of Highway，1992，12(4):27-33.

［5］折學森.路基涵洞的土壓力計算［J］.中國公路學報，1992，5(3):32-39.ZHE Xue-sen.The calculation of vertical earth pressure on buried conduit under roadbed［J］.China Journal of Highway and Transport，1992，5(3):32-39.

［6］GB 50332—2002給水排水工程管道結構設計規范［S］.北京:中華人民共和國建設部，2002.

［7］GB 50253—2003輸油管道工程設計規范［S］.北京:中國計劃出版社，2003.

［8］Prevost R C，Kienow K K.Basic of flexible pipe structural design［J］.Jourmal of Transportation Engineering，1994，120(40):652-671.

［9］莊茁，張帆，岑松，等.ABAQUS非線性有限元分析實例［M］.北京:科學出版社，2005.

［10］CECS 141—2002給水排水工程埋地鋼管管道結構設計規程［S］.北京:中國工程建設標準化協會，2002.

［11］王直民.交通荷載作用下埋地管道的力學性狀研究［D］.杭州:浙江大學，2006.

［12］黃清猷.地下管計算［M］.武漢:湖北科學技術出版社，1987.