高速公路養護預算定額測定對象的優選方法

叢卓紅，吳正鶯，鄭南翔，李小東

(1.長安大學道路施工技術與裝備教育部重點實驗室，陜西西安710064;

2.長安大學公路學院，陜西西安710064;3.重慶高速公路集團有限公司，重慶401121)

0 引言

預算定額的測定與編制主要是通過在施工現場中測定施工中消耗的工、料、機數量而實現。一個待測定的依托工程含有多個標段，每個標段同時存在多個施工隊組作業。在實際的觀測過程中，考慮到由于各施工隊組勞動生產水平的差異可能導致結果的可用性差，為避免大量人力物力財力的浪費則需要在眾多施工隊組中選擇合適的觀測對象，這是測定定額數據之前必須解決的關鍵性問題，也是決定采集的數據有效性的重要步驟［1］。筆者采用基于層次分析的模糊綜合評價法來進行養護定額測定對象的優選。

1 基于層次分析的模糊綜合評價法

模糊綜合評價法是一種基于模糊數學的綜合評價方法，該綜合評價法根據模糊數學隸屬度理論把定性評價轉化為定量評價，即用模糊數學對受到多種因素制約的事物或對象做出一個總體的評價。它具有結果清晰，系統性強的特點，能較好地解決難以量化的、模糊的問題，適合各種非確定性問題的解決［2］。

層次分析法的主要思路是將所要分析的問題層次化，根據問題的性質和所要達到的總目標，將問題分解為不同的組成因素，并按照這些因素間的相互關聯影響以及隸屬關系將因素按不同層次聚集組合，形成一個多層次分析結構模型。最后將該問題歸結為最低層相對最高層(總目標)的比較優劣的排序問題［2］。

結合高速公路養護定額測定對象特點，采用基于層次分析法的模糊綜合評價法進行優選定額觀測對象是一種科學、有效的評價方法。

2 模糊綜合評價基本原理與方法步驟

選擇的對象好與不好，一般情況下沒有固定不變和絕對分明的界限，要從眾多個測定對象中選擇最優者作為目標，則需要通過多標準來衡量這個目標是否達到，模糊綜合評價就是把模糊數學應用到判別事物和系統優劣領域的新方法。

2.1 確定評價對象的因素論域

評價因素即方案受評指標，評價因素論域為:

式中:U為評價因素論域;ui為評價因素(i=1，2，…，n)

測定對象的評價涉及到的因素很多，因此要根據養護單位的實際情況抓住主要因素。筆者通過對各養護公司的調研與專家討論，確定的各養護分公司的評價因素有養護作業經驗、養護機械設備情況、現場管理水平、工人技術水平4個主要方面，測定對象評選系統結構如圖1。

圖1 最優對象評選系統結構圖Fig.1 Optimal object selection system structure

2.2 確定評價因素的權重

以圖1為例，采用層次分析法進行計算，先把評價因素進行兩兩對比，構成兩兩對比結果的判斷矩陣［3-6］。即

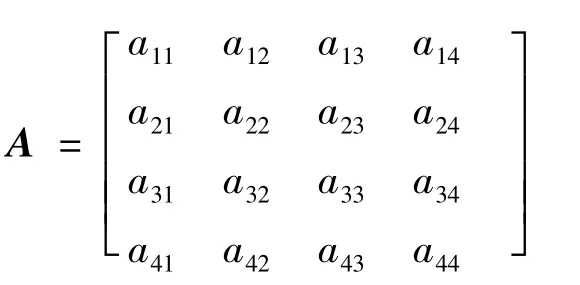
其中:aij＞0，aji=1/aij，aii=1(i，j=1，2，3，4，5)，aij通常取 1，2，3，4，5，6，7，8，9 及其倒數。

表1 層次分析法因素重要性評判標度Tab.1 Importance evaluation scale of analytic hierarchy process factors

根據判斷矩陣A計算其相應最大特征根λmax，ai，使之滿足

式中:W 為評價因素的權重向量，W=(w1，w2，w3，w4)T采用和積法求解［6］。對判斷矩陣A的每一列正規化:

將A=(aij)n×n按行加總，然后將上一步所得行和向量正規化，得權重向量n1，2，...，n ，再將，求得最大特征值λmax。其中:(AWi)表示A· W的第i個分量，A· W= λmax· W存在。

最后進行一致性檢驗。

只有當判斷矩陣完全一致時，判斷矩陣才存在λmax=n;而不一致時，λmax＞n。故以λmax-n差值大小來判斷一致性程度，用CI這一指標:

其中:λmax為矩陣最大特征根;n為矩陣階數。CI越小說明一致性越好。同時，必須具有滿意的一致性，要將CI與平均隨機一致性指標RI比較，得出檢驗值 CR［5］:CR=CI/RI，RI值見表 2。

表2 平均隨機一致性指標Tab.2 Random consistency index of exponential scale

若CR＜0.10，視兩兩對比判斷矩陣A的估計基本一致，即認為矩陣的一致性可以接受。若CR≥0.10，視兩兩對比判斷矩陣A的估計不一致，需要重新調整陣A的值，重新估計。

2.3 確定測定對象評價等級

測定對象評價等級應理解為模糊等級，一般可取5個等級，好(Y1)、較好(Y2)、一般(Y3)、較差(Y4)、差 (Y5)，其集合為 Y={Y1，Y2，Y3，Y4，Y5}［7］。

2.4 確定各測定對象的復合模糊子集

對于每一測定對象，分別確定其決策模型。

其中:tij為某一測定對象單因素評價下的隸屬函數值

綜合評價時，采用隸屬頻率值進行計算［8］。例如:有15位專家對某一養護單位的作業經驗進行評價時，有9位評價好，3位評價較好，3位評價一般，則其隸屬頻率值分別為 0.6，0.2，0.2，0.0，0.0。如此進行可得某一測定對象T，則該測定對象的復合模糊子集為:

其中:p1，p2，p3，p4，p5為該測定對象的最終評價結果。

為了方便計算，引入虛擬分值，根據實際情況需要將各評價等級賦予相應的分值(f1，f2，f3，f4，f5)，比如說對等級 Y1，Y2，Y3，Y4，Y5分別賦予(5，4，3，2，1)的分值。則可計算出各測定對象的評價結果虛擬總分如下:

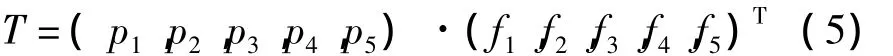
2.5 測定對象的選擇

定額編制要滿足平均先進性原則。平均先進水平是指在正常的施工條件下，大多數施工隊組和大多數生產者經過努力能夠達到和超過的水平。一般說它應該低于先進水平，而略高于平均水平，它是編制定額的理想水平。

選擇其作業經驗、養護設備、現場管理、工人技能等方面的綜合模糊評價水平滿足平均先進水平的養護單位為養護定額測定對象，由此測定編制的定額水平使先進者感到一定的壓力，使處于中間水平的工人感到定額水平可望可及，對于落后工人不遷就，使他們意識到必須花大力氣去改善施工條件，提高技術操作水平。按照基于層次分析的模糊綜合評價法得到各測定對象的最終評價結果，分別計算量化成的虛擬分值，最后采用二次平均法進行最佳選擇，根據實際情況需要，選擇若干個與最優測定對象水平相當的養護單位為測定對象。最優對象選擇具體步驟如下:

2)將分值高于平均分的測定對象選出(U1，U2，…，Uk)，k＜n，計算其平均值 h1;

3)計算二次平均值h1=(h+h1)/2;

4)計算Δhi=|hi-h1|，選擇滿足Δhi最小的對象Gi即為最優測定對象。

3 實例計算

為方便說明，將本例中各養護站分別記為G1，G2，G3，G4。

1)每個養護站的評價因素為作業經驗、養護設備情況、現場管理水平、工人技術水平，即評價因素層為Ai=(A1，A2，A3，A4)=(作業經驗，養護設備，現場管理，工人技能)。

2)采用層次分析法確定權重。結合實際，通過專家或者決策者來決定判斷矩陣的值。各評價因素兩兩對比，構成兩兩對比結果的判斷矩陣如下:

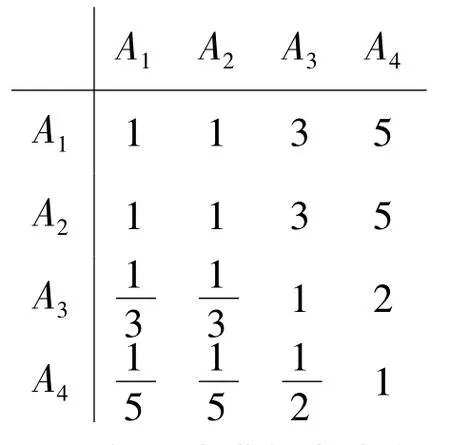
采用和積法求解判斷矩陣，計算評價因素的組合權重和最大特征值并進行一致性檢驗。具體做法是首先求出判斷矩陣各列元素之和，再用各列元素分別除以本列元素之和，得出標準化矩陣，然后求出此標準化矩陣各行的平均值，即為該評判因素的權重。λmax的計算是將所得權重與判斷矩陣相應列元素相乘，所得矩陣的行和分別與權重相除，所得商的平均值即為特征值。也可以采用MATLAB軟件直接計算。得到權重向量為:

W=(0.393 5，0.393 5，0.137 6，0.075 4)T

則λmax的計算過程如表3。

表3 λmax計算過程Tab.3 Calculation process of λmax

則 λmax=(4.007+4.007+4.002+4.000)/4=4.004

最后進行一致性檢驗:

所以該判斷矩陣滿足一致性檢驗，可以接受。

3)確定各測定對象的復合模糊子集

對各分公司 G1，G2，G3，G4，其模糊決策模型見表4。其中隸屬函數值的確定針對各個分公司不同的實際情況，收集相關調查資料，通過主觀權重法(AHP)和客觀權重法(變異系數法)組合賦權決定［9］。

表4 模糊決策模型Tab.4 Fuzzy decision-making model

4)計算綜合評價

同理，可計算:

分組，計算 h1=(4.336+4.476)/2=4.406

計算二次平均值:h1=(4.193+4.406)/2=4.299 5

可知 U2-h1=4.336-4.299 5=0.036 5 最小，故，在此選對象2為最優對象。

5)計算虛擬總分

同理，可計算:

U2=4.336，U3=4.173，U4=4.476

6)確定最優對象——計算平均分值

4 結語

在眾多的養護單位中如何選擇合適的測定對象是測定定額數據之前必須解決的關鍵問題，也是決定采集的數據有效性的重要步驟［1］。選擇合適的高速公路養護定額測定對象對定額編制有著重大的意義。

筆者全面考慮影響優選養護單位的各種因素，建立了評價測定對象的因素論域，運用層次分析法確定了評價對象因素論域中各因素的權重，較好地保證了權重系數的準確性，結合模糊綜合評價法，確定各測定對象的復合模糊子集，確定最優對象，選擇測定對象范圍。應用模糊綜合評價法，可以在數據不充分條件下體現評價因素和評價過程的模糊性，同時可以減少因個人主觀臆斷而帶來的弊端，比一般的評價方法更符合客觀實際，能夠比較客觀地評定養護定額各測定對象的實際施工情況，使我們對各測定對象的評價由定性到定量，具有較強的科學性，對實際工程具有一定的指導意義。

［1］李林軼.模糊綜合評價在橋涵補充定額編制中的應用研究［D］.西安:長安大學公路學院，2009.

［2］汪應洛.系統工程理論、方法及應用［M］.北京:高等教育出版社，1998.

［3］慕金波.層次分析法在評定最優環境工程方案中的應用［J］.環境科學進展，1997(4):33-40.MU Jin-bo.Application of analytical hierarchy process method for selecting the optimal environmental engineering science［J］.Advances in Environmental Science，1997(4):33-40.

［4］孫東生，朱懿，周水興.基于指數標度的層次分析法在橋梁評定中的應用［J］.重慶交通大學學報:自然科學版，2010，29(6):867-870.SUN Dong-sheng，ZHU Yi，ZHOU Shui-xing.Application of exponential scale of AHP in bridge evaluation［J］.Journal of Chongqing Jiaotong University:Natural Science，2010，29(6):867-870.

［5］Saaty T L.An exposition of the AHP in reply to the paper remarks on the analytic hierarchy process［J］.Management Science，1990，36(3):259-268.

［6］曾蓉，陳洪凱，李俊業.熵權模糊綜合評價法在公路洪災危險性評價中應用［J］.重慶交通大學學報:自然科學版，2010，29(4):587-591.ZENG Rong，CHEN Hong-kai，LI Jun-ye.Fuzzy comprehensive evaluation method based on entropy in road flood risk assessment［J］.Journal of Chongqing Jiaotong University:Natural Science，2010，29(4):587-591.

［7］王旭，霍德利.模糊綜合評價法在煤礦安全評價中的應用［J］.中國礦業，2008，27(5):75-78.WANG Xu，HUO De-li.Application of fuzzy comprehensive evaluation in coal safety assessment［J］.China Mining Magazine，2008，27(5):75-78.

［8］何夕平.模糊綜合評價在選擇最優施工方案中的應用［J］.合肥工業大學學報:自然科學版，2000，23(6):1050-1054.HE Xi-ping.Application of fuzzy comprehensive evaluation to selecting the optimal construction plan［J］.Journal of Hefei University of Technology:Natural Science，2000，23(6):1050-1054

［9］李玉琳，高志剛，韓延玲.模糊綜合評價中權值確定和合成算子選擇［J］.計算機工程與應用，2006，23(5):38-43.LI Yu-lin，GAO Zhi-gang，HAN Yan-ling.The determination of weight value and the choice of composite operators in fuzzy comprehensive evaluation［J］.Computer Engineering and Application，2006，23(5):38-43.