臺風狀態下碼頭護舷受力與吸能特點分析
李永超 楊 啟
(上海交通大學船舶海洋與建筑工程學院 上海 200240) (海洋工程國家重點實驗室 上海 200240)
系泊狀態下的船舶在海浪、潮流、風等動力因素的聯合作用下,運動量較平常急劇增大,纜繩和護舷承受極限載荷的概率也隨之增大,導致斷纜、船舶破損或護舷結構物破壞等事故也會增多.在風、波浪和水流的聯合作用下,系泊系統內部在外載荷的作用下發生相互作用,船舶會在6個自由度下運動,即縱蕩、橫蕩、垂蕩、橫搖、縱搖、艏搖.除了環境載荷,系泊船舶有時還會受到過往船只,潮汐等因素的影響.而且由于纜繩和護舷材料的非線性,纜繩的松弛與張緊,防護舷的接觸與否,都對系泊系統的計算分析造成很大難度.
文獻[1]通過對系泊船舶的研究,利用蒙特卡洛算法、混沌解法對碼頭系泊船舶纜繩張力進行了數值模擬,并與試驗結果進行了對比分析,得到較好的一致性.文獻[2]采用模矢搜索的方法求解了風、浪、流作用下系泊船的系纜力,并與蒙特卡洛算法進行了分析比較,討論了不同水位和不同風浪流夾角對系纜力的影響.不足之處在于,對護舷的變形-反力曲線采用的是線性模擬,本文在模矢搜索的基礎上,對護舷的模擬采用三次樣條插值,更加真實的反映了護舷的變形與吸能狀況,并討論了不同浪流夾角下護舷的受力變化情況.
1 坐標系的建立
為了描述系泊船舶的運動,建立如圖1所示的坐標系,XOY與水平面重合,X軸與船體中線重合,坐標原點位于船舯處.
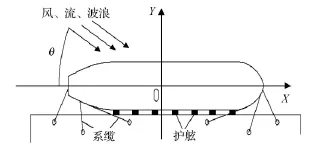
圖1 系泊船舶的坐標系
2 船舶的環境載荷
臺風來襲時,船舶的環境載荷主要有風壓力、水流力和波浪力,三者對護舷承受的撞擊力以及纜繩的系纜力都有著重要的影響.本文中,風壓力、水流力的計算在OCI MF提供的資料[3]中有詳細的論述.對于波浪力,一階力采用弗勞德-克雷諾 夫 假 設 (Fr oude-Kr yl ov)[4],二 階 力 采 用Daidola提出的經驗公式[5],詳細請況見文獻[2].這樣,綜合上述的風壓力,水流力,波浪力,就可以計算出一定條件下的環境力.
3 纜繩以及護舷的模擬
3.1 船舶受到的纜繩拉力
系泊船舶在環境載荷作用下,偏離原有的位置,使纜繩強迫伸長,纜繩長度的變化引起纜繩張力的變化.纜繩的張力可以直接使用Wilson公式進行計算
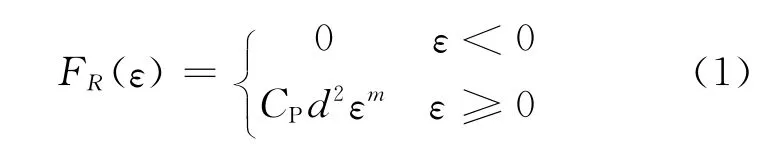
式中:CP為纜繩彈性系數,CP=1.56×104N/mm2;d為纜繩的直徑,mm;ε為纜繩應變,ε=ΔL/L,ΔL為纜繩的變形長度,L為纜繩的長度;m為指數,與纜繩的材料有關,對于尼龍纜取3,鋼絲繩取3/2.
假設船舶受到一定的環境力,偏離了原有位置,導致纜繩強迫伸長,如圖2所示.
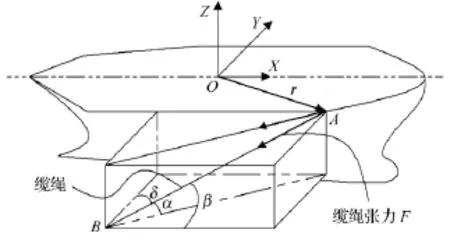
圖2 纜繩拉力示意圖
從圖2中可以看出,對于第i根纜繩,設纜繩原長為Loi,導纜孔的坐標為 Ai=[Xai,Yai,Zai],帶纜樁的坐標為Bi=[Xbi,Ybi,Zbi],則纜繩的應變為
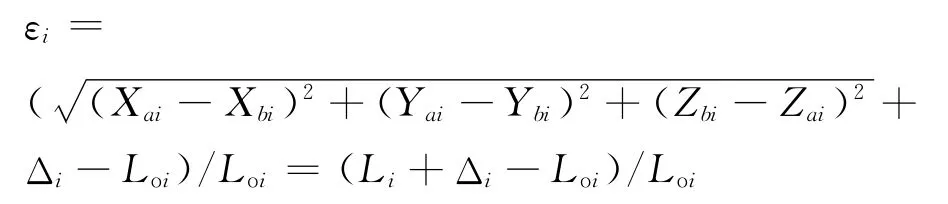
式中:Δi為第i根纜繩對應的導纜孔Bi到系泊絞車的距離;Loi是指船舶位于初始位置時,纜繩的原長度,量取的起點是船上的帶纜樁或者系泊絞車,經過導纜孔,終點是碼頭上的帶纜樁.
纜繩的拉力由式(1)可知
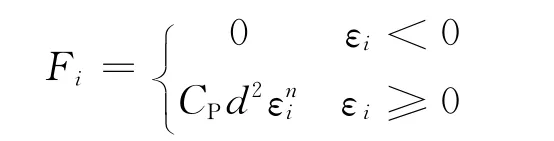
纜繩拉力在X,Y軸上的投影可以寫為
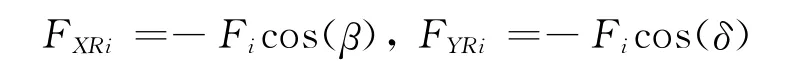
纜繩拉力在XOY平面內對O點的力矩為
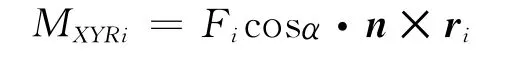
式中:n為與Fi同方向的單位向量;cosα=Li;cosβ= (Xai-Xbi)/Li,cosδ= (Yai-Ybi)/Li.
若有n根纜繩,則所有纜繩的總效果表示為
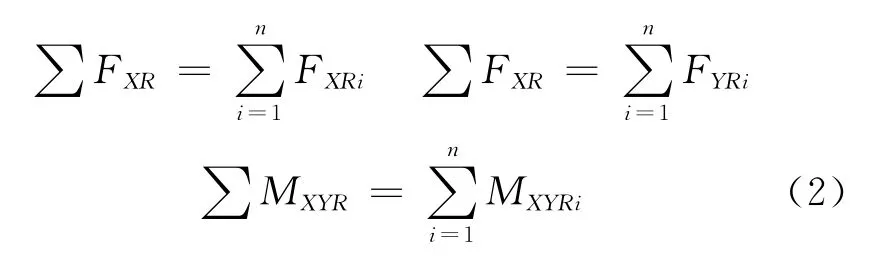
3.2 護舷的反力計算
本文中采用三次樣條插值,模擬護舷反力和變形之間的關系.如圖3所示,根據選取樣點的個數,Ffend(ε)是一個分段三次多項式,若用Fi(ε)表示Ffend(ε)在第i個子區間[εi-1,εi]上的表達式,則Fi(ε)有如下形式
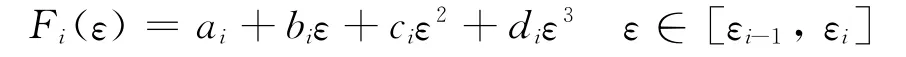
那么,對于任意的形變量ε,就可以表示為
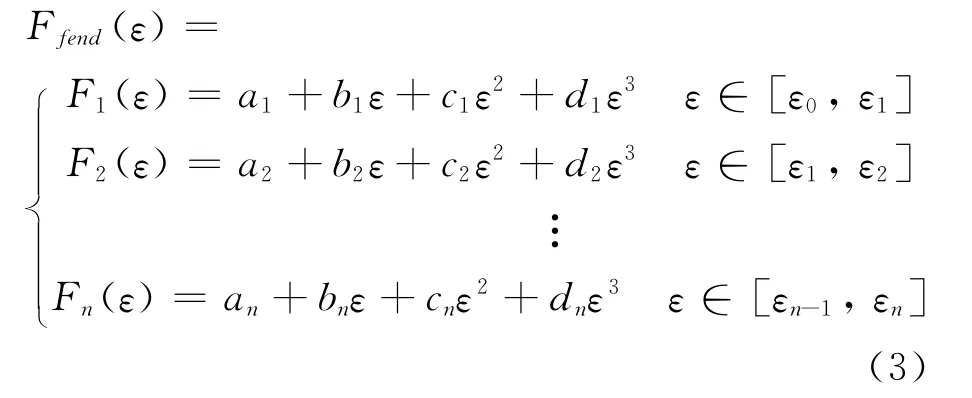
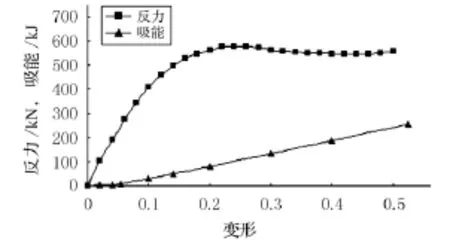
圖3 護舷形變-反力模擬
對于第j根護舷,若有εj,則由式(3)有對應的Ffendj(εj).
假設在圖1的坐標系下,總共有K只護舷,護舷的坐標為[X1,X2,X3,…,XK],不計及護舷的摩擦等因素,護舷受到壓縮后,只產生Y方向上的作用力,所以有
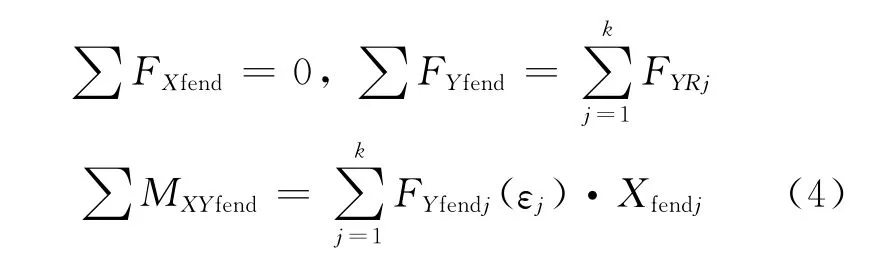
4 數學模型的建立以及求解
4.1 數學模型的建立
考慮到系泊船舶靜態平衡時,船舶受到的環境力、纜繩拉力、護舷反力,在X方向和Y方向的合力以及力矩的矢量和為零,由式(2)、(4)得總的平衡方程可以為

式中:FXE,FYE,MXYE分別為X 方向上的環境力、Y方向上的環境力和首搖力矩,根據2中介紹的方法求得.
4.2 方程的求解
由于系泊纜繩的彈性拉伸是一個非線性過程,同時護舷橡膠材料的非線性,使得方程求解變得非常困難.本文利用模矢搜索方法進行.在文獻[2]和[6]中,比較詳細的論述了模矢搜索的原理以及過程,在此直接給出如下結果.
如圖4所示,系泊狀態下,船舶受到一定的環境載荷后,偏離初始位置,經過3個自由度的變化后,發生平動和偏轉,位移矢量記為(x,y,θ).
護舷受力以及纜繩的張力,都是(x,y,θ)的函數,于是得到如下的目標函數
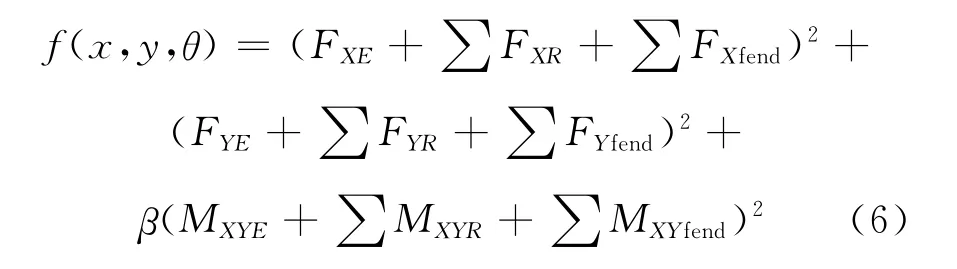
當船舶達到靜態平衡時,應滿足方程(5),此時有f(x,y,θ)=0.求解過程中,只要使得f(x,y,θ)<10-3,即可得到符合要求的(x,y,θ),此時的位置即為船舶的平衡位置.
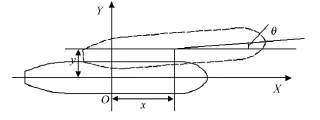
圖4 自由度變化圖示
5 算例與分析
5.1 算例
計算時的環境載荷選用2009年登陸我國廣州臺山的“巨爵”號臺風,當時一艘大型絞吸式挖泥船正系泊于深圳港,受臺風影響,導致護舷與船體受力過大而損壞,本文采用當時的實測資料計算.計算時的環境載荷為:風速15 m/s,流速2 kn,波高1.2 m,碼頭水深為12 m,船舶吃水5.8 m,船寬12 m,垂線間長97.5 m.護舷為鼓形護舷,雙層布置,設計變形量為52%,最大反力值為560 k N.如圖5所示,纜繩的編號為R1~R7,護舷的編號為H1~H6,風、浪和流的方向與X軸負方向夾角為正.
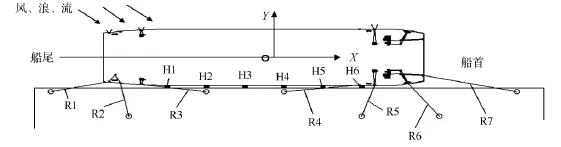
圖5 天鯨號系泊示意圖
為了顯示護舷受力與波流相互作用的規律,數據分組如下:(1)A1組纜繩預張力為0,風、浪與X軸負方向夾角0~180°,在風、浪角度確定后,不斷變換流與X軸負方向夾角,并計算護舷和纜繩應力;(2)A2,A3,A4與A1相同,只是纜繩的預張力分別為50,100,200 k N.為了敘述方便,當風浪與X軸負方向夾角90°,流與X軸負方向夾角90°時記為(90°,90°),下文類似的情況不再說明.表1僅給出A1中的風、浪角度為90°時的計算結果,其余0,15,30°等未給出.
5.2 纜繩預張力的影響
在A1~A4中計算了纜繩處于不同預張力時,在各種風浪和流角度下的系泊力.將護舷受力超出其設計極限的風浪流的角度組合挑選出來,繪制成如圖6所示,當風浪方向落入黑色區域,而水流方向落入斜線區域時,就可能會發生護舷破壞的情況.由圖6中可見,在一定范圍內,纜繩預張力越大,危險區域越小,護舷發生破壞的可能性也就越小.
事實上,加大纜繩的預張力,會使護舷的受力更加均勻.如圖7所示,在風、浪與X軸負方向夾角落入圖6所示的危險區域時,即風、浪角度為75°,隨著預張力的不同,護舷受力均方差發生的變化.圖7中A點表示:風、浪與X軸負方向夾角75°,流向與X 軸負方向夾角60°,此時 H1~H6六個護舷受力的均方差為240 k N.為了顯示護舷受力的不均勻性,選2組比較危險的風浪流組合,A2中的(75°,90°)和(105°,90°),在這2種浪流組合下計算各個護舷受力,如圖8所示,在預張力為50 k N時,船首和船尾的護舷反力較大,容易遭到破壞.
通過上述比較可以看出,纜繩預張力在一定范圍內增加,會減少護舷遭到破壞的幾率,但在危險狀況下,預張力的增加對護舷受力的均勻性改善并無多大效果.

表1 風、浪角度90°時護舷受力隨流角度的變化
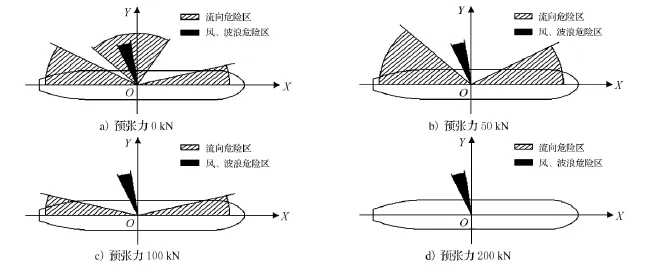
圖6 纜繩預張力的影響
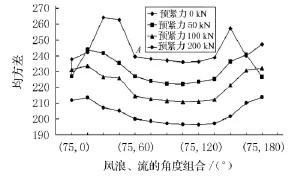
圖7 護舷受力的均方差
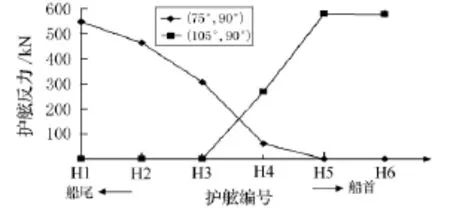
圖8 護舷反力變化圖
5.3 護舷的吸能特點
護舷的選取不僅要考慮其反力的大小,還要考慮護舷的吸能大小.為了比較不同護舷的性能,選取2種護舷型號,計算危險狀況下護舷的反力與吸能.圖9給出了2種護舷的力學特性,雖然二者達到設計極限時反力幾乎相同,但是在相同反力時,DF-SC鼓形護舷的吸能小,變形小,而DFCY圓筒型護舷的吸能高,變形大,二者均采用三次插值函數進行模擬.
計算條件如下:纜繩預張力50 k N,風、浪角度75°,順流;風、浪角度90°,橫流;風、浪角度105°,橫流.計算結果見表2.
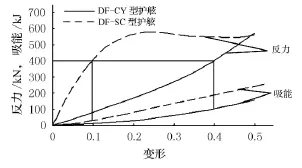
圖9 護舷力學特性
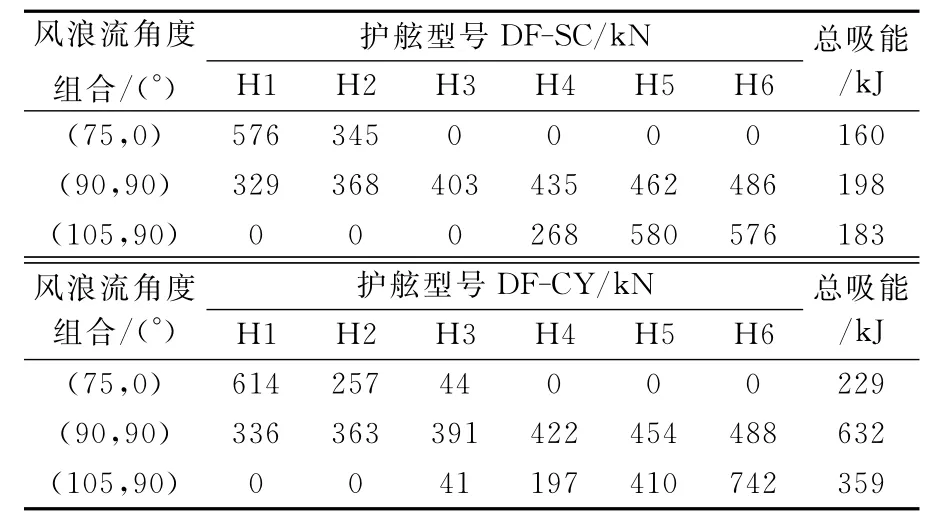
表2 兩種護舷的計算結果
從表中可以看出,兩種護舷反力都已接近或者超過了極限值,但是DF-CY型護舷吸能高,也就意味著此種護舷的緩沖性能較好.
6 結束語
本文對臺風狀態下系泊船舶的環境載荷做了詳細分析,并建立和求解了系泊平衡方程.對如何選取和布置護舷有一定的指導意義.在求解方程的過程中,對模矢搜索的護舷模擬進行了改進,采用三次樣條函數擬合護舷的變形-反力曲線,使得計算結果更貼近工程和實際.計算結果表明,臺風來臨時,提高纜繩的預張力,有利于系泊系統的平穩性,護舷遭到破壞的可能性降低,在危險狀況下,應對船首和船尾的護舷進行特別加固.從保護船體的觀點出發,在經常遭受臺風襲擊的港口,宜布置吸能高,反力高型護舷.
[1]向 溢.碼頭智能系泊系統研究[D].上海:上海交通大學船舶與海洋工程學院,2001.
[2]楊 啟,李 臻.基于模矢搜索船舶系泊評價函數[J].上海交通大學學報,2007,41(2):221-226.
[3]OCI MF.大型船舶在直碼頭和島式碼頭安全系泊的建議和準則[M].宋昭和,傅祿儀,譯.London:OCI MF,1979.
[4]劉應中,繆國平.船舶在波浪上的運動理論[M].上海:上海交通大學出版社,1987.
[5]李向群.多點系泊船舶在波浪中的運動及其系泊力[J].交通部上海船舶運輸科學研究所學報,1999,22(1):9-15.
[6]秦士元.系統分析[M].上海:上海交通大學出版社,1987.

