善用“四動” 培養(yǎng)數(shù)學(xué)思維能力

邱詠梅

（泰寧市水南小學(xué)，福建 泰寧 354400）

小學(xué)生思維能力的發(fā)展，需要有一個長期的培養(yǎng)和訓(xùn)練過程。由于小學(xué)生的思維還處于具體形象思維占優(yōu)勢的階段，而數(shù)學(xué)又是一門抽象性和邏輯性很強的學(xué)科，要解決數(shù)學(xué)學(xué)科抽象性與小學(xué)生思維的具體形象性之間的矛盾，行之有效的方法是讓學(xué)生多種感官參與數(shù)學(xué)的學(xué)習(xí)過程。因此，在教學(xué)中我們要有意識地結(jié)合教學(xué)內(nèi)容，重視學(xué)生獲取知識的思維過程，讓學(xué)生做到“動眼觀察、動手操作、動腦思考、動口表達”四方面有機的結(jié)合，從而掌握數(shù)學(xué)知識，培養(yǎng)學(xué)生數(shù)學(xué)思維的能力。

一、動眼觀察，啟迪思維

“觀察是思維的開端和源泉”。由于小學(xué)生的思維比較簡單、形象、直接，只看表面不能深入里層，需要通過不斷的觀察誘導(dǎo)，才能理解抽象的數(shù)學(xué)知識。因此，必須讓學(xué)生對具體形象的事物、圖片、教具進行有目的的觀察，在觀察過程中獲取數(shù)學(xué)知識。

例如，教學(xué)第一冊《認識幾何圖形》（一）時，老師可先引導(dǎo)學(xué)生觀察實物。如長方形紙、課本封面、課桌面、黑板面、正方形紙等，指出它們的形狀都是長方形或正方形，接著將學(xué)生課前準備的幾何圖形與實物一一對照，讓學(xué)生知道圖形的名稱，再引導(dǎo)學(xué)生仔細觀察生活中還有哪些物體的面是這樣的形狀。通過觀察，讓學(xué)生進行異中求同、同中辨異的思維訓(xùn)練，區(qū)分近似對象，然后加以抽象，畫出長方形、正方形的平面圖形，讓學(xué)生明白長方形和正方形都有四條邊，但正方形是四條邊一樣長的長方形，而長方形只有相對的兩條邊相等。這樣，由具體到抽象，引導(dǎo)學(xué)生通過觀察實物，物形對照，感知形體，初步建立長方形、正方形的表象，從而培養(yǎng)了學(xué)生的觀察能力和空間想象能力，促進了思維能力的提高。

二、動手操作，激活思維

操作是智力的源泉，思維的起點，也是培養(yǎng)學(xué)生技能、技巧、促進思維發(fā)展的一種手段。在教學(xué)中，我們要發(fā)揮數(shù)學(xué)學(xué)科可以動手操作這一優(yōu)勢，多讓孩子們動手操作，讓他們在實踐中充分感知，在動手中展開思維，通過手腦并用，建立清晰鮮明的表象，從而培養(yǎng)學(xué)生的抽象思維能力。

例如，教學(xué)“三角形的內(nèi)角和等于180度”，這個定理若直接給出，學(xué)生也會做題，但學(xué)生只是“知其然而不知其所以然”。如果讓學(xué)生自己動手把銳角三角形的三個角撕下（或剪下）拼在一起，結(jié)果得到一個平角，當(dāng)繼續(xù)把鈍角三角形、直角三角形的三個內(nèi)角分別撕下拼在一起，又是平角時，終于明白、理解了“三角形的內(nèi)角和等于180度”的定理。這樣，學(xué)生通過動手操作，既開拓了學(xué)生思維的靈活性，又增強了獲得知識的深刻性，也為學(xué)生以后的學(xué)習(xí)留下了必要的知識空間。

由此可見，操作活動是學(xué)生獲取知識的重要途徑，也是教學(xué)的有效手段之一。老師要把每一個學(xué)生的操作看作是他的思維的動態(tài)反映，當(dāng)學(xué)生明確操作目的，恰當(dāng)運用學(xué)具，操作方法得當(dāng)時，就顯示他們的思維是準確、有序、清晰的。

三、動腦思考，拓展思維

愛因斯坦說過：“學(xué)習(xí)知識要善于思考、思考、再思考，我就是靠這個學(xué)習(xí)方法成為科學(xué)家的”。因此，在數(shù)學(xué)教學(xué)中，我們要以思考為中心，以多思為手段，以樂思、善思為目標，通過激發(fā)學(xué)生思考的活力，調(diào)動學(xué)生的思考積極性，培養(yǎng)學(xué)生敢于思考、善于思考，逐步養(yǎng)成有條理、有根據(jù)地思考問題的良好習(xí)慣。而小學(xué)生碰到疑難問題往往不會想或不愿意想，老師在課堂上必須嚴格要求學(xué)生養(yǎng)成樂思的習(xí)慣，學(xué)生的思維必須緊跟著老師的講授，對老師的每一發(fā)問做出積極的反應(yīng)。在課堂上要給他們“想”的機會，留有“想”的余地，更要教給他們“想”的方法，以此來拓展學(xué)生的思維。

例如，教學(xué)“三角形的內(nèi)角和是180度”后，我出了這樣一道題：“根據(jù)三角形的內(nèi)角和是180度，你能求出四邊形和正六邊形的內(nèi)角和嗎？”題目一出現(xiàn)，學(xué)生非常感興趣，但無從下手，這時，我啟發(fā)學(xué)生：“能不能將四邊形分割成兩個三角形，再想辦法呢？并讓學(xué)生小組討論。通過討論交流，共同得出了：將四邊形分割成兩個三角形，兩個三角形的內(nèi)角和相加，也就是2個180度相加等于360度。而正六邊形可以分割成四個三角形，它的內(nèi)角和就是4個180度，也就是720度。

通過這樣的練習(xí)，拓展了學(xué)生的思維，培養(yǎng)了學(xué)生思維的敏捷性和深刻性。

四、動口表達，深化思維

數(shù)學(xué)語言表達能力的強弱，直接關(guān)系到學(xué)生對數(shù)的概念、基本算理、計算方法等知識的理解。在教學(xué)中，我們要盡可能創(chuàng)造條件，給學(xué)生“說”的機會，啟發(fā)學(xué)生動口把看到的、想到的清楚地表達出來，一方面是讓學(xué)生把內(nèi)部知識轉(zhuǎn)化為外部語言，另一方面是把外部的知識內(nèi)化成學(xué)生自己的知識。這是“思維的動作”與“動作的思維”相結(jié)合的過程。

1.引導(dǎo)學(xué)生多說

語言和思維有著密切聯(lián)系，人們借助語言思考問題，表達思維。所以，訓(xùn)練語言是培養(yǎng)思維能力的重要途徑。例如，在教學(xué)一年級的圖畫應(yīng)用題時，應(yīng)啟發(fā)學(xué)生積極看圖編題，理解題意。可以要求學(xué)生練習(xí)這樣一道題：

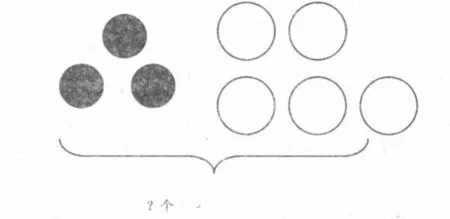
學(xué)生經(jīng)過認真思考，從不同角度編出了很多道應(yīng)用題：①原來有3個圓，又拿來5個圓，一共有幾個圓？②從左右看：左邊有3個黑圓，右邊5個白圓，求一共有幾個圓？③從大小看：小圓有3個，大圓有5個，一共有幾個圓？④從顏色看：黑圓有3個，白圓有5個，一共有幾個圓？……學(xué)生編題后，教師還緊追不舍，要求學(xué)生說出解題思路。應(yīng)該說，解答應(yīng)用題讓學(xué)生談解題思路是至關(guān)重要的，因為解題正確，不一定思路清晰、思維方法正確，而通過讓學(xué)生說，使教師獲得有用的反饋信息，又便于教師了解學(xué)生的理解程度，可以有的放矢地進行點撥，提高其思維水平。

2.培養(yǎng)學(xué)生精說

在表達思維過程中，要提高學(xué)生結(jié)合具體題目，用自己理解的語言來說一說，以后逐步用比較精練的語言來表述。如：“草地上有3只小鴨，小雞的只數(shù)是小鴨的5倍，小雞有多少只？”教學(xué)這道題時，可讓學(xué)生學(xué)會表述：小雞的只數(shù)是小鴨的5倍，也就是小雞只數(shù)里有5個3，求小雞的只數(shù)也就是求5個3只是多少，用5×3＝15，以后又精練到一句，就是“求5個3是多少？”言簡意賅、擊中要害，避免了解題中簡單的對號入座，機械套用，又培養(yǎng)了學(xué)生思維的敏捷性。

總之，在教學(xué)中運用“四動”，能使學(xué)生的多種感官處于積極的活動狀態(tài)，真正體現(xiàn)以學(xué)生為主體，既符合學(xué)生年齡特點，又提高了學(xué)生參與學(xué)習(xí)的興趣，開闊了學(xué)生視野，拓寬了學(xué)生思路，使學(xué)生思維能力不斷提高。