一種基于ESO的導(dǎo)彈魯棒自動駕駛儀設(shè)計方法①

董飛垚，雷虎民，邵 雷，張金鵬

(1.空軍工程大學(xué)導(dǎo)彈學(xué)院，三原 713800;2.中國空空導(dǎo)彈研究院，洛陽 471009)

0 引言

針對飛行器控制過程中存在的干擾和未建模特性，近年來，國內(nèi)外學(xué)者展開了廣泛研究［1－7］。文獻［1］基于增益調(diào)度思想設(shè)計了飛機的一種自動駕駛儀，但針對高速飛行器，采用該方法系統(tǒng)的快速性和魯棒性變得較差;文獻［2］依據(jù)H∞控制理論設(shè)計的導(dǎo)彈魯棒自動駕駛儀具有很好的魯棒穩(wěn)定性能，但是其控制器形式過于復(fù)雜，限制了其實際工程應(yīng)用;文獻［3］采用最優(yōu)控制來保證系統(tǒng)的快速性和魯棒性，但是反饋所需的狀態(tài)量在實際工程中并不都能獲得;文獻［4］通過設(shè)計一種基于滑模理論的干擾觀測器來增強系統(tǒng)的魯棒性，但其控制律設(shè)計中需要已知系統(tǒng)不確定性的上界，保守性很大，且容易引起控制量的飽和問題。擴張狀態(tài)觀測器(ESO)是將系統(tǒng)中含有的非線性動態(tài)、模型不確定性及外界擾動等都視為擴張狀態(tài)加以觀測，其本身并不依賴于生成擾動的具體模型，也不需要直接去測量其作用，是通用的擾動觀測器［8］。

本文提出了一種基于擴張狀態(tài)觀測器的導(dǎo)彈滾轉(zhuǎn)自動駕駛儀設(shè)計方法，保證導(dǎo)彈在大機動和強干擾下具有較好的動態(tài)性能和強魯棒性。

1 非線性擴張狀態(tài)觀測器

考慮如下一類n階SISO非線性系統(tǒng):

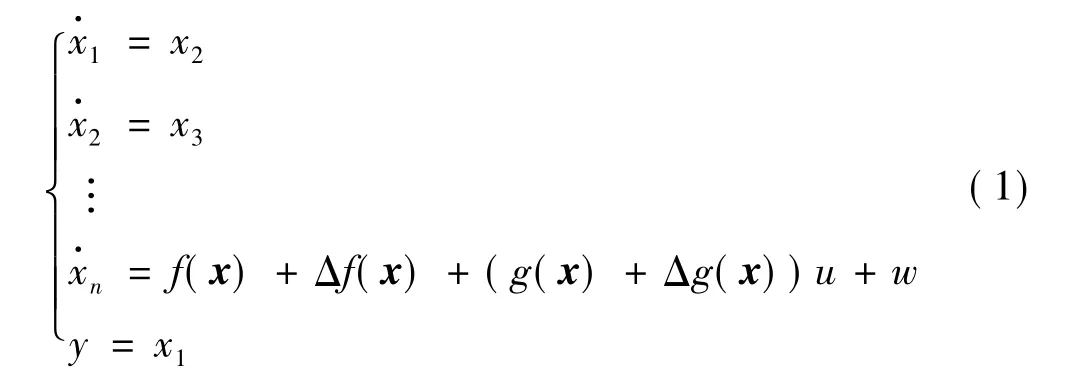
式中 x=［x1x2… xn］T表示系統(tǒng)的狀態(tài);?(x)和g(x)為已知標(biāo)量函數(shù);Δ?(x)、Δg(x)和w表示未知不確定性和外界擾動;u為控制輸入;y為系統(tǒng)輸出。

定義d=Δ?(x)+Δg(x)+w為作用于系統(tǒng)的復(fù)合干擾，并將其作為系統(tǒng)(1)的一個擴張狀態(tài)xn+1，則系統(tǒng)(1)可擴展為n+1階系統(tǒng):

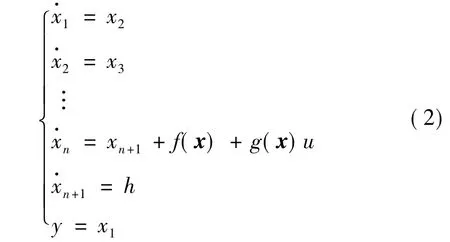
針對上述系統(tǒng)，采用如下非線性觀測器(NESO):

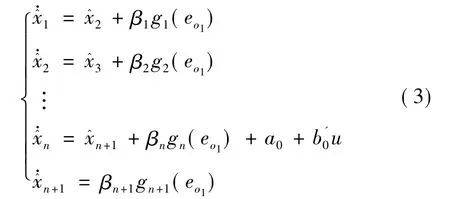
可見，只要βi和gi選擇恰當(dāng)，狀態(tài)估計值就能精確逼近實際值xi，即→xi。所以gi的選擇極其關(guān)鍵，目前大多采用如下帶有線性區(qū)的非光滑函數(shù)［9］:

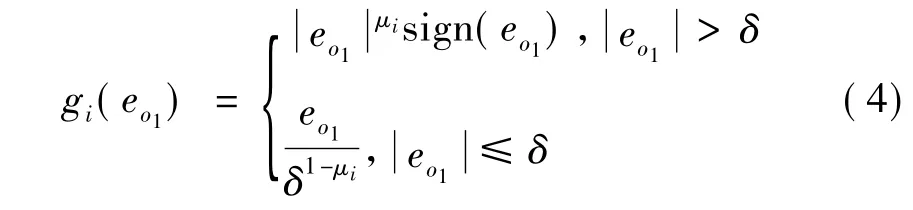
其中，0 ＜μi＜1，i=1，2，…，n+1，δ＞0 為 gi切換的閾值。可以看出，函數(shù) gi的一個重要特性是當(dāng)誤差較小時，gi有較大值，相反當(dāng)誤差較大時，gi具有較小值。

2 模型描述

導(dǎo)彈滾轉(zhuǎn)通道控制系統(tǒng)由速率陀螺、舵機和控制算法等組成。其中速率陀螺用來測量導(dǎo)彈的滾轉(zhuǎn)角速率，進而通過積分獲得滾轉(zhuǎn)角，舵機用來響應(yīng)由控制算法生成的副翼偏角指令，形成副翼偏角，產(chǎn)生相應(yīng)滾轉(zhuǎn)力矩，抑制和消除彈體滾轉(zhuǎn)。

舵機一般可用二階模型來描述:

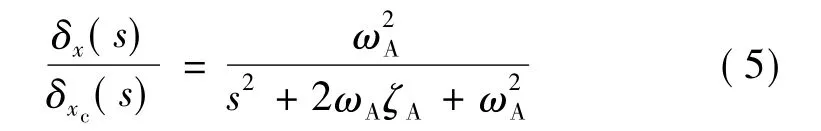
式中 δx和δxc分別為副翼偏角和副翼偏角指令;ωA和ζA分別為舵機的自然頻率和阻尼。

根據(jù)文獻［10］，不考慮俯仰、偏航和滾轉(zhuǎn)通道耦合情況，導(dǎo)彈滾轉(zhuǎn)通道的剛體數(shù)學(xué)模型可寫成:

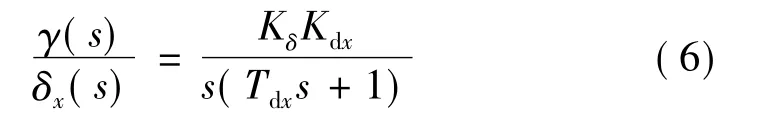
式中 γ為導(dǎo)彈輸出滾轉(zhuǎn)角;Kδ為導(dǎo)彈副翼效率系數(shù);Kdx和Tdx分別為導(dǎo)彈滾轉(zhuǎn)傳遞系數(shù)和滾轉(zhuǎn)時間常數(shù)。

聯(lián)立式(5)和式(6)，可得從副翼偏角指令δxc到導(dǎo)彈滾轉(zhuǎn)角γ的傳遞函數(shù):

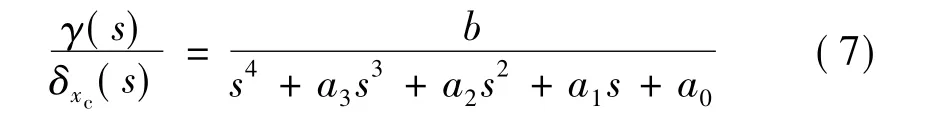
式中 b=KδKdxω/Tdx，a0=0，a1= ω/Tdx，a2=(Tdxω+2ωAζA)/Tdx;a3=(1+2ωAζATdx)/Tdx。

考慮到空氣動力系數(shù)的不確定性，ai(i=1，2，3，4)和b并不能精確獲得，所以 ai=ai0+Δa，b=b0+Δb，其中ai0和b0表示所對應(yīng)系數(shù)的標(biāo)稱值，Δa和Δb表示相應(yīng)的不確定性。此外，為了后續(xù)仿真驗證，給出彈性彈體和速率陀螺的模型，分別為G1(s)和G2(s):

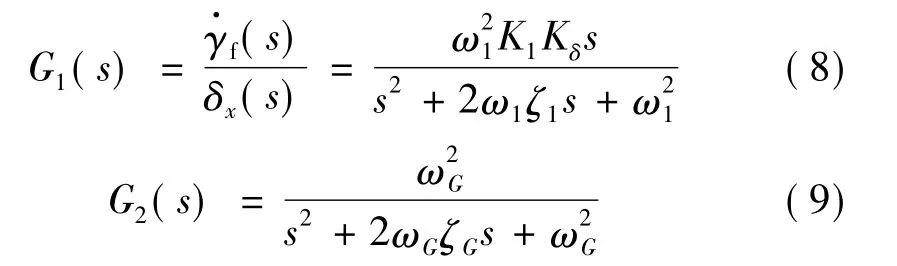
以上模型參數(shù)的取值如表1所示，表中det為等效外界擾動。

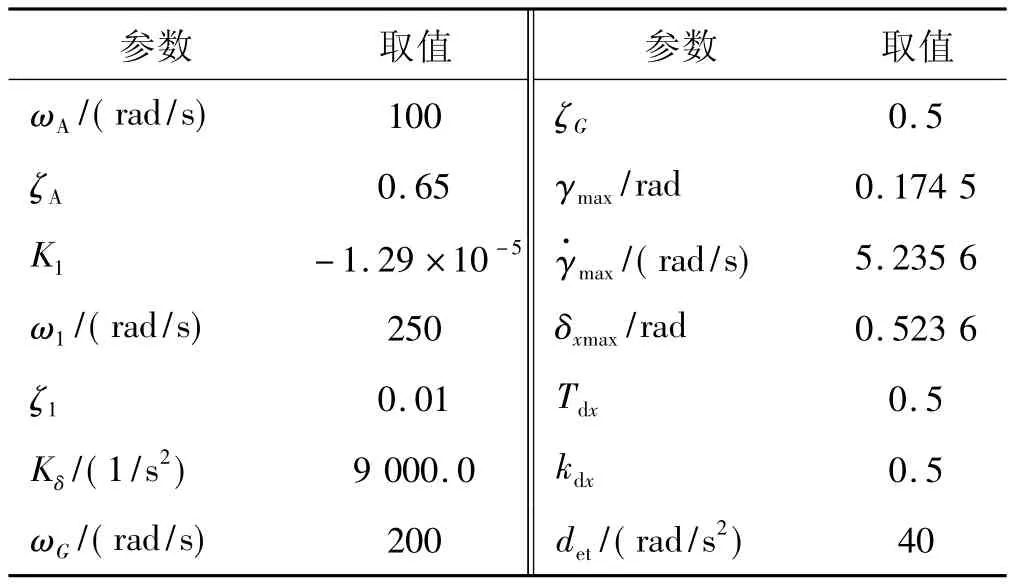
表1 各模型參數(shù)數(shù)值表Table 1 Value of parameters in each model

3 控制算法設(shè)計及穩(wěn)定性分析

為便于分析和設(shè)計，將式(7)寫成如下形式:

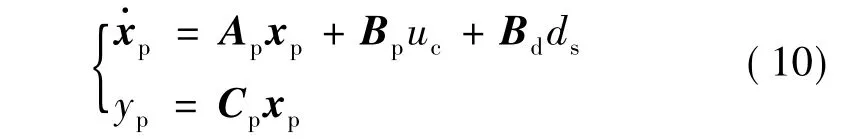
式中 x=［x1x2x3x4］T表示系統(tǒng)狀態(tài);uc=δx為控制輸入;yp=γ為系統(tǒng)輸出;Bd為干擾輸入匹配矩陣;ds=φ－Δa1x1－Δa2x2－Δa3x3－Δa4x4+Δbu，表示作用于系統(tǒng)的復(fù)合干擾，φ為外界擾動;Ap、Bp和Cp分別為系統(tǒng)矩陣、輸入矩陣和輸出矩陣。

Ap、Bp、Bd和 Cp表達式如下:

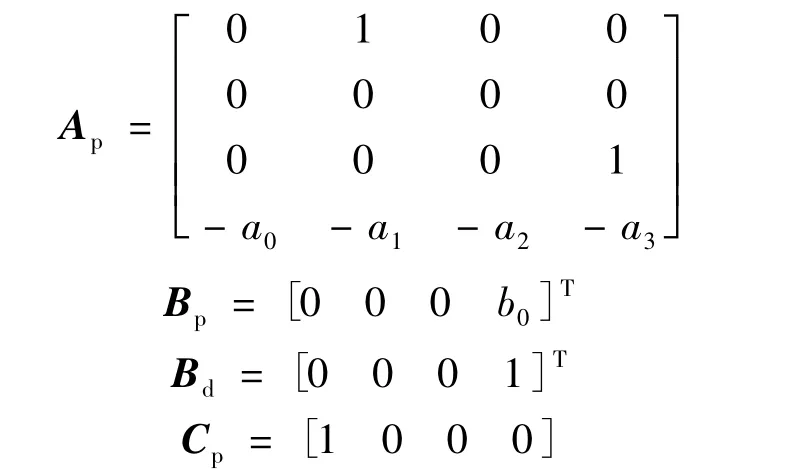
同式(2)，若將ds作為系統(tǒng)的一個擴張狀態(tài)x5，則式(10)可擴展為

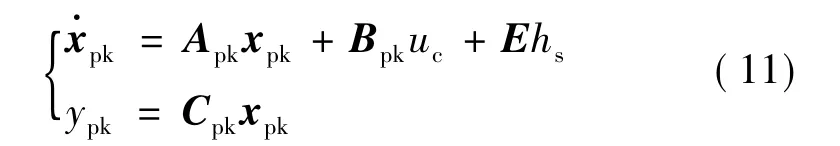
其中: xpk= ［x1x2x3x4x5］T

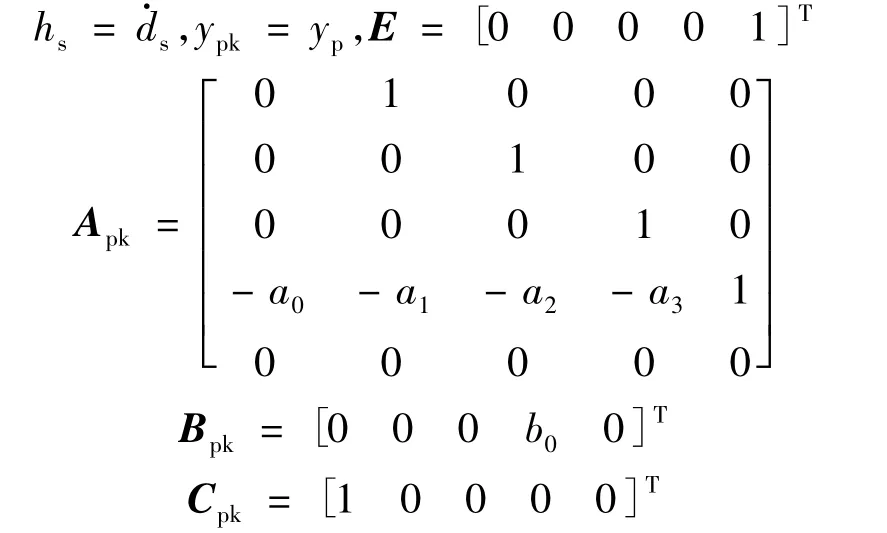
容易判斷(Ap，Bp，Cp)可控可觀測，根據(jù)文獻［11］，若被控系統(tǒng)可控可觀測，用狀態(tài)觀測器估計值形成狀態(tài)反饋時，其系統(tǒng)的狀態(tài)反饋設(shè)計和觀測器設(shè)計可分別獨立進行。所以可先進行系統(tǒng)的控制算法設(shè)計。

3.1 控制算法

本文基于ESO所設(shè)計的控制算法包含兩部分，分別是針對標(biāo)稱系統(tǒng)的最優(yōu)控制項uc1和針對系統(tǒng)復(fù)合干擾的補償項uc2。

針對標(biāo)稱系統(tǒng)，采用線性二次型調(diào)節(jié)器(LQR)進行控制，設(shè)計控制信號uc1，使得目標(biāo)函數(shù)J取得最小值，J通常取如下形式:

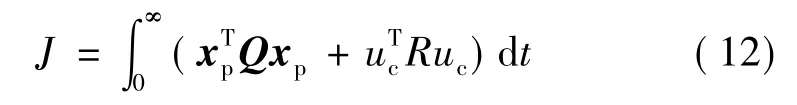
式中 Q和R為所選擇的加權(quán)矩陣和加權(quán)系數(shù)。

Q陣所有元素均非負，R為大于0的實數(shù)，分別取Q 和 R 為［12］

通過求解代數(shù)Riccati方程:

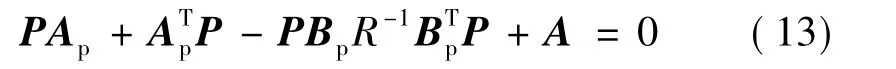
便可得J取得最小值的解:

控制信號中干擾補償項uc2取

將uc=uc1+uc2代入式(10)可得

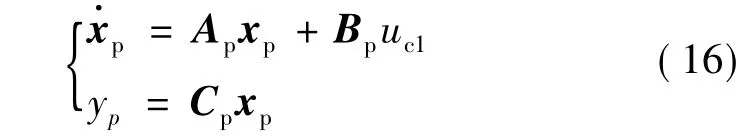
所以uc能保證系統(tǒng)(10)對外界擾動和自身未建模動態(tài)具有強魯棒性。

依據(jù)文獻［13］，當(dāng)系統(tǒng)存在未知干擾和未建模動態(tài)時，利用觀測狀態(tài)設(shè)計的控制系統(tǒng)，其性能要優(yōu)于直接利用系統(tǒng)實際狀態(tài)所設(shè)計的控制系統(tǒng)。而且在導(dǎo)彈的實際飛行過程中，xp和ds并不能直接獲取。為此引入ESO完成對系統(tǒng)狀態(tài)的估計并將估計狀態(tài)值用于狀態(tài)反饋。

結(jié)合式(3)和式(11)，取 gi(eo1)=eo1，得

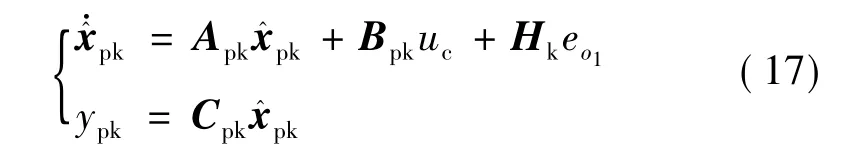
式中 Hk=［β1β2β3β4β5］為待確定的觀測增益向量，通過式(17)可完成對系統(tǒng)狀態(tài)的估計。

3.2 穩(wěn)定性分析

如上節(jié)所述，因彈性或外界擾動帶來的偏差，可在控制信號中加以補償。根據(jù)式(17)所估計狀態(tài)，控制算法為

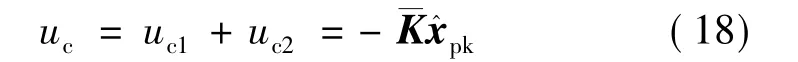
將式(17)代入式(8)得

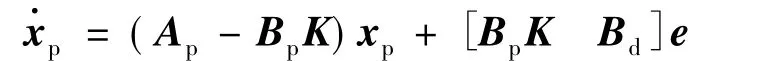
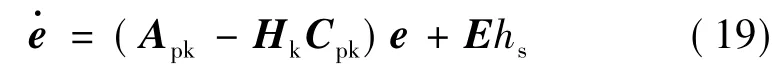
聯(lián)立式(18)和式(19)得

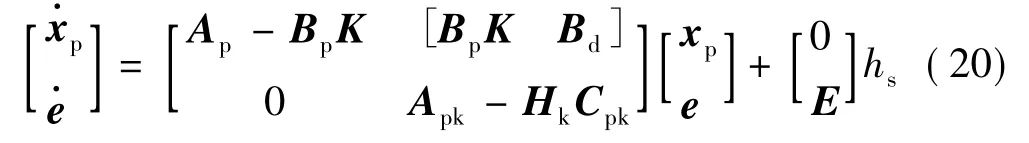
由式(20)可看出，其系統(tǒng)矩陣為三角塊矩陣，故其特征值僅由主對角線上各矩陣塊的特征值決定，即由Ap－BpK和Apk－HkCpk的特征值決定。

根據(jù)上節(jié)的分析，Ap－BpK的特征值均具有負實部，所以若Apk－HkCpk的特征值具有負實部，則系統(tǒng)(20)漸近穩(wěn)定。

由以上分析可知，保證系統(tǒng)穩(wěn)定的前提是矩陣Apk－HkCpk的特征值具有負實部，而矩陣Apk－HkCpk的特征值可任意配置的前提是(Apk，Cpk)可觀測。

下面證明(Apk，Cpk)亦可觀測。

證明:定義 ei，i=1，2，…，5 為第 i行元素為 1，其他行元素均為0的列向量，則Apk和Cpk可分別表示為

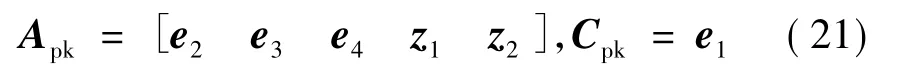
式中 z1和z2分別為的第4列和第5列。

可觀測性判定矩陣V如下所示:

不難發(fā)現(xiàn)，rank(V)=5，故(Apk，Cpk)可觀測。

由于(Apk，Cpk)可觀測，故矩陣 Apk－HkCpk特征值可任意配置。Hk陣參數(shù)的選取應(yīng)遵循觀測器響應(yīng)速度比狀態(tài)反饋系統(tǒng)的響應(yīng)速度快的原則［8］。不難求解，依據(jù)控制算法式(14)，標(biāo)稱系統(tǒng)的極點被配置在－30，－202，－104.24±j182.91。由于其主導(dǎo)極點為－30，所以將矩陣Apk－HkCpk特征值配置在－45，便可得到觀測矩陣Hk。

4 仿真結(jié)果及分析

為了便于驗證本文所設(shè)計的控制算法的優(yōu)越性，分別在以下3種情形下進行仿真:情形一為標(biāo)稱狀態(tài);情形二為僅考慮彈性干擾;情形三為同時考慮彈性干擾、外界擾動和陀螺的動態(tài)特性。仿真中模型參數(shù)取表1中的數(shù)值，系統(tǒng)初始狀態(tài)設(shè)為:xp0=［5° 0 0 0］，仿真結(jié)果見圖1～圖4。

針對標(biāo)稱系統(tǒng)，利用系統(tǒng)的實際狀態(tài)進行反饋，采用LQR控制，系統(tǒng)具有良好的動態(tài)性能，消除5°初始滾轉(zhuǎn)角所需調(diào)節(jié)時間不大于0.15 s，且副翼偏角小于其最大容許值，如圖1(a)所示;但考慮彈性干擾時，若仍采用LQR控制，系統(tǒng)將不穩(wěn)定，如圖1(b)所示。

基于Luenberger全維狀態(tài)觀測器(LO)對系統(tǒng)狀態(tài)估計，并將估計值用于LQR控制中，當(dāng)僅考慮彈性干擾時，系統(tǒng)漸近穩(wěn)定，如圖2(a)所示;但若同時考慮彈性干擾和外界擾動的情況下，基于LO狀態(tài)觀測器的LQR控制不但不能消除初始滾轉(zhuǎn)角，反而使其增大到超過10°，如圖2(b)所示。

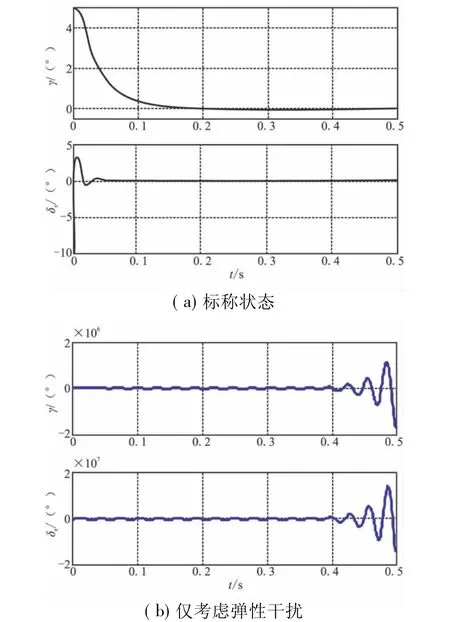
圖1 采用LQR時γ和δx變化曲線Fig.1 Curves of γ and δxwith LQR

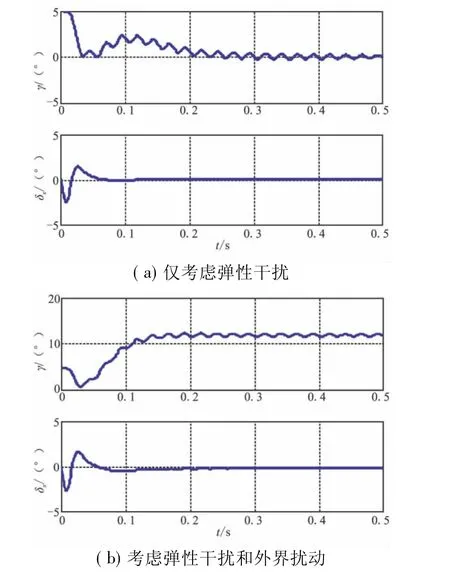
圖2 采用LQR+LO時γ和δx變化曲線Fig.2 Curves of γ and δxwith LQR+LO

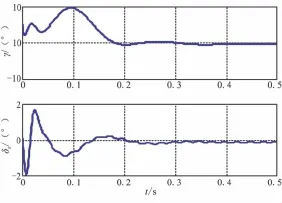
圖3 情形三下采用LQR+ESO時γ和δx變化曲線Fig.3 Curves of γ and δxwith LQR+ESO in No.3 condition

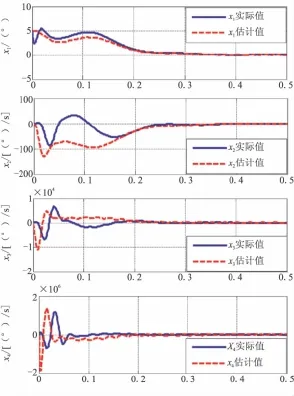
圖4 情形三下ESO系統(tǒng)狀態(tài)估計值與實際值比較圖Fig.4 Comparison between estimated value with ESO and actual value in No.3 condition

圖3和圖4為同時考慮彈性干擾、外界擾動和陀螺的動態(tài)特性情況下的部分輸出曲線，可看出，ESO狀態(tài)觀測器能準(zhǔn)確估計系統(tǒng)的實際狀態(tài)和復(fù)合干擾，基于ESO估計狀態(tài)的控制算法能消除彈性和外界擾動等因素帶來的影響，保證滾轉(zhuǎn)角在最短時間內(nèi)收斂于零，且副翼偏角在其最大容許值以下。此外，在情形三下，取表1中模型參數(shù)40%的攝動值，基于ESO估計狀態(tài)的所設(shè)計的LQR控制算法同樣具有較好的控制效果，但由于篇幅所限，這里未能給出相應(yīng)曲線。

5 結(jié)論

本文設(shè)計了一種基于ESO的導(dǎo)彈滾轉(zhuǎn)魯棒自動駕駛儀設(shè)計方法。仿真結(jié)果表明，在同時考慮彈性干擾、外界擾動和陀螺動態(tài)特性的情況下，所設(shè)計ESO狀態(tài)觀測器能準(zhǔn)確估計系統(tǒng)的狀態(tài)及干擾，控制算法能消除復(fù)合干擾帶來的影響，具有良好的動態(tài)特性和強魯棒性，從而克服了傳統(tǒng)設(shè)計方法的缺陷，能保證導(dǎo)彈在高機動和強干擾下滾轉(zhuǎn)通道的快速穩(wěn)定。

［1］Lee C H，Shin M H，Chung M J.A design of gain-scheduled control for a linear parameter varing system:an application to flight control［J］.Control Engineering Practice，2001，32(9):11-12.

［2］Tan F，Duan G R，Zhao L J.Robust controller design for autopilot of a BTT missile［C］//Proc.of the 6th World Congress on Intelligent Control and Automation.2006(21-23):6358-6362.

［3］Kumaresan N，Balasubramaniam P.Optimal control for stochastic linear quadratic singular system using neural networks［J］.Journal of Process Control，2009，19(7):482-488.

［4］Hall C E，Shtessel Y B.Sliding mode disturbance observerbased control for a reusable launch vehicle［C］//AIAA Guidance Navigation and Control Conference and Exhibit.Reston:AIAA，2005:1-26.

［5］White B A，Bruyere L，Tsourdos A.Missile autopilot design using quasi-Lpv polynomial eigenstructure assignment［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(4):1472-1483.

［6］Batool Labibi，Horacio J M，Chen T W.Decentralized robust output feedback control for control affine nonlinear interconnected systems ［J］.Journal of Process Control，2009，19(3):865-878.

［7］Trottemant E J，Scherer C W，Weiss M，et al.Robust missile feedback control strategies［J］.Journal of Guidance，Control，and Dynamics，2010，33(6):1837-1846.

［8］韓京清.自抗擾控制技術(shù)［M］.北京:國防工業(yè)出版社，2008:183-197.

［9］Gao Z Q，Huang Y，Han J Q.An alternative paradigm for control system design［C］//Proceedings of IEEE Conference on Control and Decision.Orlando，2001:4578-4585.

［10］錢杏芳.導(dǎo)彈飛行力學(xué)［M］.北京:北京理工大學(xué)出版社，2008:248-255.

［11］胡壽松.自動控制原理［M］.北京:科學(xué)出版社，2005:489-491.

［12］Nesline F W，Wells B H，Zarchan，P.Combined optimal classical approach to robust missile autopilot design［J］.Journal of Guidance，Control and Dynamics，1981，4(3):316-322.

［13］Zaks S H，Brehove J D，Corless，M J.Control of uncertain systems with unmolded actuator and sensor dynamics and incomplete state information ［J］.IEEE Transcations on Systems.Man and Cybernetics，1989，19(2):241-257.