艦載導彈發射數值模擬與點火時機研究①

陳余軍，姜 毅，趙剛練

(北京理工大學宇航學院，北京 100081)

0 引言

在艦船上發射導彈，受海情的影響艦船姿態具有動態隨機性，任意時刻和狀態下的發射得到的導彈出筒姿態幾乎都不相同，根據制導與控制系統對導彈出筒姿態參數的要求［1］，需要對各種環境和條件下的發射出筒姿態進行預估，為制導控制系統的設計提供參考，對武器系統的設計與評估有重要意義。隨著艦載武器的發展，國內外學者已在相關技術領域展開了相關研究，齊強等［2］基于理論力學方法建立運動方程組分析海情變化對導彈初始彈道的影響;于存貴等［3］基于Adams軟件分析了艦載火箭炮在不同海況下的射擊精度;段齊駿等［4］運用船舶耐波性理論，并結合概率與數理統計原理研究了艦載武器裝備發射精度與載體運動的關系。目前研究多數基于理論力學方法討論載體運動及海況對武器發射精度的影響，對于武器發射極限狀態及時機選擇的研究幾乎空白。

本文圍繞艦載導彈發射問題，重點分析艦載發射的惡劣狀態以及導彈出筒姿態與海況、推力、發射點及發射時刻之間的關系。考慮到計算工況縱多，文中將利用成熟而高效的商業軟件Adams平臺，通過模型參數化和腳本語言實現艦載導彈發射過程的自動化仿真和數值試驗，找出最惡劣的發射狀態和較合理的發射條件和窗口，為彈上控制系統設計和發射控制提供綜合性參考。

1 動力學仿真建模

1.1 模型簡化

考慮到導彈發動機點火失敗引起的發射安全性問題［5］，艦載導彈武器系統通常采用準垂直方式(通常向側舷傾斜小于5°)發射。本文選取垂直自推力不同時離軌的艦載發射系統為設計對象，依據多體動力學原理對艦載導彈發射系統進行簡化，簡化后的系統由導彈、前后滑塊、導軌、發射筒和艦船等構件組成。艦載發射系統簡化模型示意如圖1所示，其中A、B分別代表靠近船頭和船尾的2個發射點。

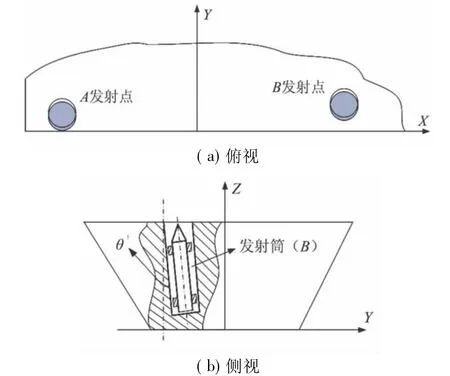
圖1 艦載發射系統示意圖Fig.1 Diagram of ship-based launch system

1.2 動力學模型

點火前導彈隨艦船一起在海浪中搖蕩，點火后導彈瞬間沿導軌運動，初始階段前后滑塊都受到約束，接著前后滑塊先后相繼滑離導軌。導彈運動經歷了全約束到半約束的過渡，由于載體的搖蕩運動以及滑塊與導軌之間的間隙因素，整個導彈發射過程的運動和受力十分復雜。

為建立動力學模型進行假設如下:

(1)所有構件均假設為剛體，不考慮結構變形對導彈運動的影響;

(2)除滑塊與導軌之間的非理想約束，其他連接均假設為理想約束;

(3)實際中導彈與船艦質量相差懸殊，并考慮到后文船艦運動描述方便，忽略發射時導彈運動對艦船運動產生的影響;

(4)為考慮更惡劣情況，為船艦初置一個橫搖和縱搖角度。

各構件之間連接關系:滑塊與導彈固連;導軌與發射筒固連;發射筒與艦船固連;滑塊與導軌之間為接觸約束。基于Adams建立多體動力學模型，作用在彈上推力由發動機點火試驗數據擬合得到，可選取不同的推進劑組分得到不同大小的推力。

為描述導彈運動，定義彈體坐標系Om-xmymzm，原點位于導彈質心，x沿彈軸并指向彈頭，z沿艦船橫搖軸方向，y根據右手坐標法則確定。記彈體角速度在彈體坐標系Om-xmymzm下沿三坐標軸方向的分量為滾轉、偏航和俯仰角速度，對應角位移則由積分得到。

1.3 動力學方程與求解

Adams采用拉格朗日乘子法建立系統動力學方程:

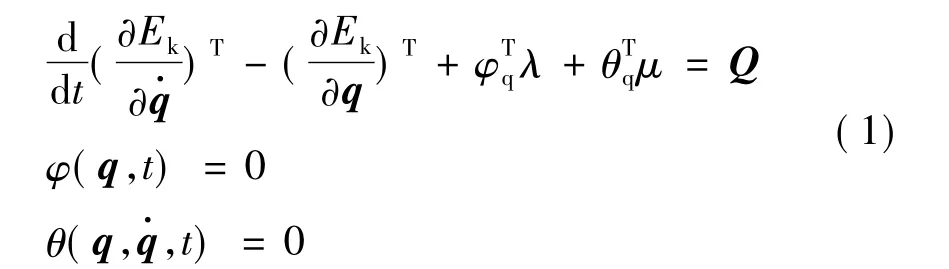
式中 Ek為系統動能;q為系統廣義坐標列陣;Q為廣義力列陣;λ為對應于完整約束的拉氏乘子列陣;μ為對應于非完整約束的拉氏乘子列陣。

采用GSTIFF積分器通過Gear預估校正算法可求解上述矩陣方程。

1.4 接觸參數設置

艦船的搖擺使得導彈上的滑塊與導軌發生接觸碰撞，從而直接影響導彈的運動規律和出筒姿態，且艦船位于不同姿態時滑塊與導軌的接觸碰撞情況也不一樣。選擇合理的間隙接觸計算模型和進行準確的參數設置是保證仿真精度的重要因素，本文采用非線性彈簧阻尼模型模擬含間隙的接觸碰撞問題，相應的接觸碰撞力計算公式［6］為

式中 Nn為兩物體間的法向作用力;?l為兩物之間的切向作用力即摩擦力;k為等效剛度系數;c(δ)為阻尼函數;δ為兩物體沿法線方向的最大穿透量;μ(vτ)為摩擦系數函數;vτ為切向相對運動速度。

滑塊和導軌的材料分別為鋼和鋁，參考軟件幫助設置參數:接觸剛度為38 000 N/mm，碰撞阻尼系數為28 N·s/mm，彈性力貢獻指數為1.5，最大穿透深度為0.1 mm，靜摩擦系數為0.3，動摩擦系數為0.1，靜摩擦轉換速度為0.1 mm/s，動摩擦轉換速度為10 mm/s。

2 艦船運動模擬

艦船的運動特性與海況、自身結構和航向有關。實際艦船在海中的運動十分復雜，為研究方便需要進行簡化，本文重點考慮艦船的橫搖、縱搖和垂蕩運動對導彈運動及出筒姿態的影響。

實際的艦船運動由多個不規則波下分運動的線性疊加組成，由于缺乏艦船的具體屬性參數，無法通過船舶耐波性原理和切片理論求解艦船在海中運動響應參數。

容易知道，越惡劣海況下導彈發射越危險，本文采用有限賦值法思想，選取搖蕩幅值及對應最小周期構成的正弦波來描述艦船運動，這樣能夠代表某級海況的極限工況，分析極限狀態下導彈的出筒姿態可作為設計的臨界條件，因此艦船的垂蕩、橫搖和縱搖運動可簡化描述為［7］

式中 ηb、γ、θ分別為垂蕩位移、橫搖位移和縱搖位移;r0、T0分別為垂蕩幅值和周期;ra、Tγ為橫搖幅值和周期;θa、Tθ為縱搖幅值和周期。

本文研究的艦載武器系統屬于大型艦船，其在4、5級海況下的搖蕩特性參數如表1所示［8］。

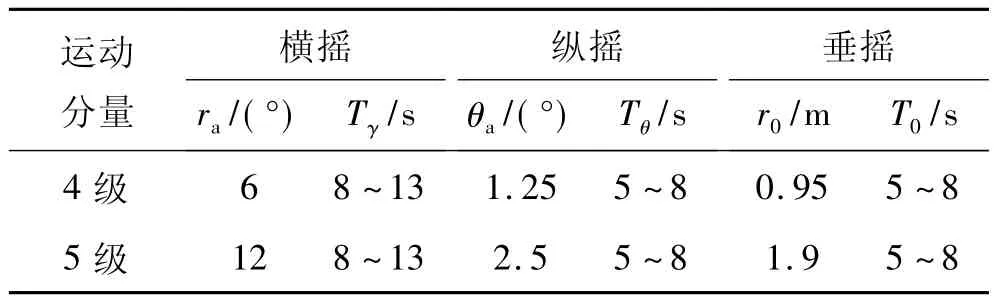
表1 大型艦船的搖蕩幅值與周期Table 1 Straying amplitude and cycle of big ship

定義與大地固連的地面全局坐標系O-xyz，原點位于艦船重心;與艦船相連的艦船坐標系Os-xsyszs，原點位于艦船重心。在上述坐標系下，通過Adams中的Point Motion工具定義艦船的6自由度運動，并根據式(4)定義艦船的橫搖、縱搖和垂蕩運動函數。容易看出，艦船的姿態與時間有關，不同時刻點火艦船位于不同姿態。

3 數值仿真試驗設計

根據表1中艦船的橫搖、縱搖和垂蕩各分運動的周期，選取最小周期描述艦船運動，在不考慮各分量初始相位情況下由最小公倍數原理得到艦船運動近似周期為40 s。為模擬艦船不同姿態下的點火，對艦船一個運動周期進行離散且每隔0.5 s進行采樣發射，對應點火時刻分別取 0、0.5、1、…、40 s，計算每 1 次發射導彈的出筒姿態，得到艦船姿態與其對應的導彈出筒姿態之間的變化規律，單個周期內單發彈的試驗總次數為81。

為考察A、B兩發射點在2種不同推力、2種不同海況下的發射特性，共需要進行發射試驗總數為81×8=648種。推力分別取為TL1和TL2，且TL1＜TL2，海況取4級和5級。

由于試驗工況和結果數據文件較多，本文通過自編程序循環調用Adams軟件的批處理命令進行動力學仿真，具體步驟為:通過程序修改模型cmd文件得到不同工況需要的模型及參數設置，在后臺通過批處理命令調用和運行cmd文件，仿真得到相應的結果數據文件，最后通過自編程序進行數據處理得到不同點火時刻導彈出筒角位移和角速度。虛擬試驗的整個計算流程如圖2所示。

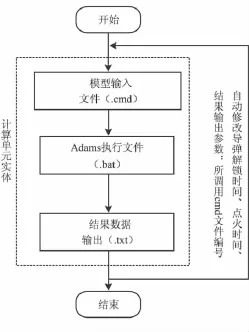
圖2 虛擬試驗流程Fig.2 Virtual experiment process

4 仿真試驗結果

通常使用角位移和角速度描述導彈運動，前者描述姿態的初始偏差，后者反映速度變化的快慢，文中選取角速度參數進行描述。

4.1 不同推力下的發射模擬

進行了5級海況下A、B發射點在TL1和TL2推力下的發射試驗，得到導彈出筒角速度隨點火時刻的變化如圖3所示。

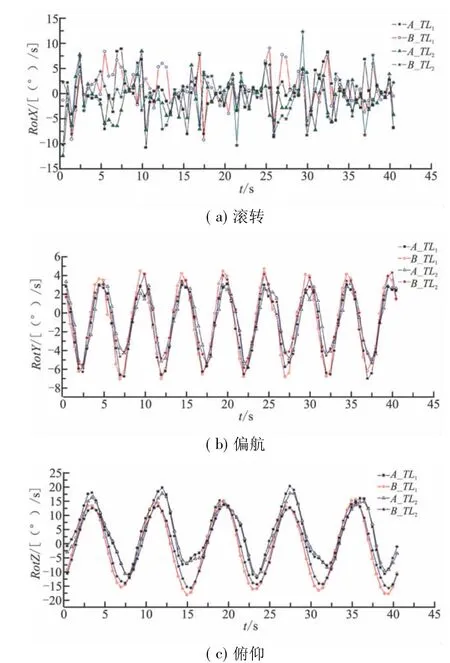
圖3 導彈出筒角速度隨點火時刻的變化曲線Fig.3 Change curves of missile outlet angular velocity with ignition time

由圖3(a)可知，滾轉角速度曲線無明顯周期特征。相同推力下，不同發射點對應最惡劣工況的點火時刻不一致，且A發射點曲線峰值較B發射點的大;同一發射點，不同推力下對應最惡劣工況的點火時刻不一致，曲線峰值與推力呈反比。滾轉姿態主要受滑塊和導軌之間的接觸碰撞影響，與離軌時刻碰撞情況直接相關;不同發射點受船艦牽連運動影響形成的碰撞程度不一致;小推力發射下導彈在軌運動時間長，與導軌接觸碰撞次數多，受牽連運動影響可能性增加。

由圖3(b)可知，偏航角速度曲線有8個波峰，曲線波動平均周期約為5 s，與艦船縱搖運動周期接近;各曲線波峰波谷對應時刻較為一致。相同推力下，B發射點曲線峰值稍大于A發射點;同一發射點，峰值與推力呈反比關系;曲線的非零對稱特性與模型中艦船的初始相位相匹配。出筒偏航姿態主要由船艦縱搖分運動的牽連運動形成，偏航姿態變化與船艦縱搖分運動規律相一致，兩者在該分量上的相對運動基本可忽略，各曲線之間的差異與發射點距離縱搖軸位置相關。

由圖3(c)可知，俯仰角速度曲線有5個波峰，曲線波動平均周期約為8 s，與艦船橫搖運動周期接近;各曲線峰值對應時刻基本接近。相同推力下，A發射點峰值稍大于B發射點;同一發射點，曲線峰值與推力呈反比;俯仰曲線非零對稱性同樣與船艦放置的初始位置相關。與偏航姿態相對應，俯仰姿態主要由船艦橫搖分運動的牽連運動產生，同樣該分量上的相對運動基本可忽略，各曲線之間差異還與發射點距離橫搖軸位置相關。

4.2 不同海況下的發射模擬

為研究海況對導彈發射出筒姿態參數的影響，對艦船在4、5級海況下的發射進行數值試驗，其中推力取TL1，得到出筒角速度峰值如表2所示。

表2 TL1下導彈出筒角速度峰值Table 2 Outlet angular velocity peak of missile under thrust TL1

由表2可知，4級海況下導彈出筒姿態角速度各分量峰值相對5級海況均有所下降，尤其是俯仰和偏航姿態，幾乎為線性變化關系，因為艦船的橫搖、縱搖峰值大小直接影響導彈的出筒偏航和俯仰姿態;不同海況下，相同推力及發射點對應的姿態曲線在不同時刻達到峰值。

為驗證仿真結果，取5級海況對應的6發彈試驗數據，其中推力TL1下A點發射對應的導彈出筒俯仰角速度最大值為22.6(°)/s、偏航角速度最大值為10.7(°)/s，滾轉角速度最大值為 12.4(°)/s，與表 2數值仿真試驗結果相比各參數在量級上基本吻合，相應的誤差則由于實際海況的復雜性難以真實模擬以及仿真模型簡化等因素形成。綜合對比情況反映出仿真模擬結果基本滿足工程精度要求，表明文中建立的數值仿真模型基本可信，可用于工程計算與分析。

5 點火時機分析

根據上述模擬結果得到，導彈出筒姿態與發射點位置、推力、海況以及發射時的艦船姿態均相關，需要根據具體發射狀態確定點火時刻。仍然選取代表導彈飛行特性的角速度參數作為點火可行的判斷指標，為考慮各姿態分量的綜合效應，進行角速度求模，得到導彈出筒角速度的模

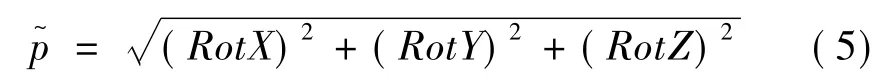
其中，右邊3項分別對應出筒時刻的俯仰、偏航和滾轉角速度分量。

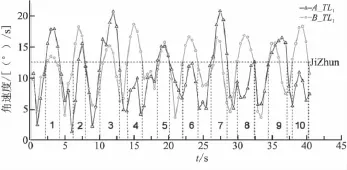
圖4 導彈出筒角速度模隨點火時刻的變化曲線Fig.4 Change curves of missile outlet angular velocity modular with ignition time

圖4反映出2條曲線波峰對應時刻基本一致，曲線的波峰和波谷基本相互交替包含，A發射點p～曲線峰值較B發射點的高。根據相應戰術指標要求，定義導彈出筒姿態角速度模低于12.5(°)/s對應的時間區間為安全點火區間，超出部分對應的時間區間定義為危險區間。由圖4曲線得到A、B發射點的公共危險點火時刻區間有 1、2、3、5、7、9，僅屬于 B 發射點危險點火時刻區間有4、6、8、10，那么在選取的發射周期內除去上述區間即為安全點火區間。

依據上述定義得到，A發射點的安全點火區間近似為(單位:s):［0，2］、［4.2，6.1］、［7.9，10］、［12.8，17.2］、［20，26.1］、［28.4，34.4］、［37，40］。B 發射點的安全點火區間近似為(單位:s):［0，2］、［4.2，6.1］、［7.9，10］、［12.8，14］、［16.1，18.3］、［20.1，22］、［24.2，26.1］、［28.4，29.8］、［32.4，34.4］、［37，38］。將這些數據載入發射控制程序，在導彈點火前瞬間實時判斷當前時刻是否在有效點火區間內，實現通過選取點火時機提高發射精度。

此外，考慮到不同分量惡劣工況對應的時刻不一致性，有必要結合制導控制系統對出筒姿態各個分量的敏感性和調控能力來確定主姿態分量，在此基礎上對上述安全點火區間進行修正，得到滿足要求的點火區間。

6 結論

(1)導彈出筒俯仰與偏航角速度主要受艦船橫搖和縱搖運動影響，其峰值與船艦的橫縱搖峰值成正比;導彈出筒滾轉角速度與滑塊和導軌之間的接觸碰撞激烈程度有關，與艦船的搖蕩運動無明顯線性關系。

(2)導彈出筒姿態參數峰值與海況級數成正比，建議選擇較低級海況進行發射;推力對導彈出筒偏航和俯仰姿態的影響不大，但與出筒滾轉角速度呈相反趨勢，在滿足相關約束條件下建議采用較大的推力發射。

(3)根據數值仿真試驗得到的惡劣狀態發射性能參數設計制導與控制系統，同時還可根據出筒姿態變化規律選擇發射窗口，但是不同發射點處的最佳點火時機需要結合推力和海況等因素來綜合確定。

［1］姚昌仁.火箭導彈發射裝置設計［M］.北京:北京理工大學出版社，1998.

［2］齊強，李善高.海情對導彈離軌姿態的影響［J］.彈箭與制導學報，2000(4):51-56.

［3］于存貴，李自勇，王惠方，等.艦載火箭炮發射動力學仿真［J］.彈道學報，2007，19(2):71-74.

［4］段齊駿，邱亞鋒，張福祥.艦載武器裝備發射精度與載體運動關系研究［J］.彈道學報，2000，12(2):60-64.

［5］岳江鋒.印度導彈及航天發射失敗的原因及影響［J］.國防科技工業，2006，9:54-56.

［6］閻紹澤，申永勝，陳洪彬.考慮桿件柔性和鉸間隙的可展結構動力學數值模擬［J］.清華大學學報(自然科學版)，2003，43(2):145-149.

［7］陶堯森.船舶耐波性［M］.上海:上海交通大學出版社，1996.

［8］趙龍波，石德平，敖百強.海清對艦空導彈離軌姿態的影響分析及補償方法［J］.現代防御技術，2008，36(6):81-85.