某型導(dǎo)彈艙段連接結(jié)構(gòu)強(qiáng)度可靠性靈敏度分析①

周 紅，劉永壽，高宗戰(zhàn)，岳珠峰

(西北工業(yè)大學(xué)工程力學(xué)系，西安 710129)

0 引言

導(dǎo)彈在空中飛行時(shí)，受氣動升力、重力等載荷共同作用，導(dǎo)彈艙段連接結(jié)構(gòu)承受一定強(qiáng)度的預(yù)應(yīng)力載荷。在氣動載荷和慣性載荷的作用下，艙段結(jié)構(gòu)可能會發(fā)生強(qiáng)度失效［1］。迄今為止，飛行器結(jié)構(gòu)設(shè)計(jì)中的強(qiáng)度、壽命分析還只是在確定性領(lǐng)域內(nèi)進(jìn)行［2－4］。事實(shí)上，對于同一批次的導(dǎo)彈艙段結(jié)構(gòu)，雖然制造的依據(jù)是同一份圖紙，但由于加工偏差等因素，使實(shí)際導(dǎo)彈艙段結(jié)構(gòu)尺寸具有一點(diǎn)隨機(jī)性，這種隨機(jī)性可從一批導(dǎo)彈艙段結(jié)構(gòu)尺寸測量得到其統(tǒng)計(jì)值。在對艙段結(jié)構(gòu)進(jìn)行強(qiáng)度分析中，盡管確定性分析是安全的，但由于結(jié)構(gòu)尺寸的隨機(jī)分散性，結(jié)構(gòu)仍有可能失效。傳統(tǒng)設(shè)計(jì)采用安全系數(shù)來給結(jié)構(gòu)設(shè)計(jì)一個(gè)較大的安全系數(shù)來確保結(jié)構(gòu)安全，雖然安全系數(shù)法在一定程度上保證了結(jié)構(gòu)的安全，實(shí)際中不能準(zhǔn)確給出安全系數(shù)的大小。可靠性及靈敏度分析可定量地給出結(jié)構(gòu)安全工作的可靠度以及影響結(jié)構(gòu)強(qiáng)度、壽命所有因素中，哪些因素是主要因素，可用于指導(dǎo)結(jié)構(gòu)設(shè)計(jì)和結(jié)構(gòu)故障預(yù)測。

本文以某型導(dǎo)彈艙段連接結(jié)構(gòu)為研究對象，采用MSC.Nastran的SOL600模塊進(jìn)行非線性接觸有限元分析，獲得艙段結(jié)構(gòu)應(yīng)力分布，分別校核各艙段結(jié)構(gòu)是否滿足設(shè)計(jì)要求。充分考慮艙段結(jié)構(gòu)尺寸參數(shù)的隨機(jī)性，建立艙段結(jié)構(gòu)在失效模式下的功能函數(shù)，將結(jié)構(gòu)可靠性分析方法與有限元參數(shù)化分析方法相結(jié)合，采用四階矩法對艙段結(jié)構(gòu)進(jìn)行可靠性和靈敏度分析，分析結(jié)果對導(dǎo)彈艙段結(jié)構(gòu)設(shè)計(jì)和制造具有一定工程意義。

1 模型和材料

艙段連接結(jié)構(gòu)如圖1所示，模型由3部分組成，左側(cè)為艙段A，右側(cè)為艙段B，艙段連接采用螺釘連接，艙段材料參數(shù)列于表1。邊界條件和載荷:艙段左端固定，右端垂直艙段向下施加6 000 N的力，每個(gè)螺釘施加1 000 N的預(yù)緊力。

圖1 某型導(dǎo)彈艙段結(jié)構(gòu)示意圖Fig.1 Diagram of a Missile Cabin Structure

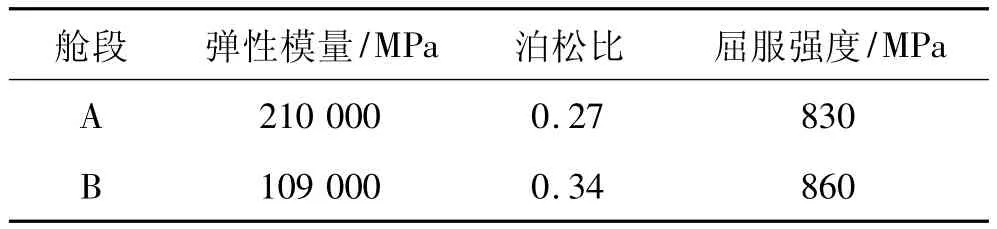
表1 艙段材料參數(shù)Table 1 Material parameter of a missile cabin structure

2 確定性分析

2.1 有限元分析

模型由MSC.Patran軟件建立，使用六面體網(wǎng)格單元對模型進(jìn)行網(wǎng)格劃分。艙段各連接結(jié)構(gòu)采用可變形體定義接觸，采用MSC.Nastran的SOL600模塊進(jìn)行非線性接觸有限元分析，后處理處理采用MSC.Patran完成，得到艙段連接結(jié)構(gòu)的應(yīng)力云圖如圖2所示。

圖2 艙段A和艙段B應(yīng)力分布云圖Fig.2 Diagram of stress distribution on cabin A and cabin B

2.2 強(qiáng)度校核

通過有限元分析發(fā)現(xiàn)，艙段A的最大應(yīng)力為395 MPa，艙段B的最大應(yīng)力161 MPa;根據(jù)艙段結(jié)構(gòu)材料參數(shù)，艙段A的屈服極限為830 MPa，艙段B的屈服極限為860 MPa。由于結(jié)構(gòu)所承受載荷、材料性能，結(jié)構(gòu)尺寸和加工質(zhì)量等存在較大分散性，為了保證結(jié)構(gòu)安全可靠，在設(shè)計(jì)中引入安全系數(shù)概念。根據(jù)飛行器強(qiáng)度設(shè)計(jì)規(guī)范，選取安全系數(shù)ns校核艙段結(jié)構(gòu)［5］，830/950，860/161均大于安全系數(shù) ns。因此，艙段結(jié)構(gòu)是安全的。

3 可靠性分析

考慮到結(jié)構(gòu)關(guān)鍵尺寸分散性對艙段結(jié)構(gòu)強(qiáng)度的影響，建立關(guān)鍵艙段結(jié)構(gòu)失效功能函數(shù)，編譯相應(yīng)的計(jì)算機(jī)程序?qū)⒔Y(jié)構(gòu)可靠性分析方法與有限元參數(shù)化分析方法相結(jié)合，能自動提取有限元分析結(jié)果，最后采用四階矩法對艙段連接結(jié)構(gòu)進(jìn)行可靠性和靈敏度分析。

3.1 隨機(jī)變量及分布

影響導(dǎo)彈艙段結(jié)構(gòu)強(qiáng)度的不確定因素主要有加工工藝和尺寸誤差，因此在對艙段結(jié)構(gòu)進(jìn)行可靠性分析時(shí)，選取部分可能會對其強(qiáng)度產(chǎn)生較大影響的參數(shù)作為隨機(jī)變量，如艙段A厚度、艙段B的厚度及螺釘孔的位置，其具體參數(shù)見表2。

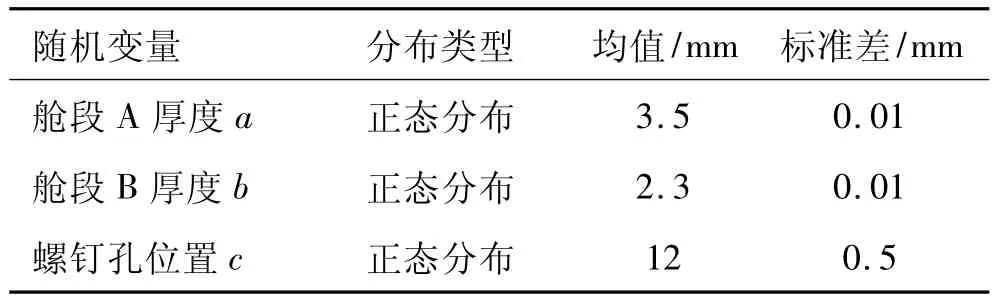
表2 隨機(jī)變量及分布類型Table 2 Random variables and distribution characters

3.2 失效模式

考慮到艙段B的最大應(yīng)力遠(yuǎn)小于其屈服強(qiáng)度，因此只考慮艙段A的強(qiáng)度失效功能函數(shù)為

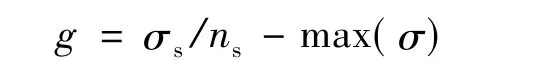
式中 g均為基本變量的隱式函數(shù)，需調(diào)用有限元軟件計(jì)算基本變量每次取值對應(yīng)的極限狀態(tài)函數(shù)值。

3.3 可靠性分析

本文采用四階矩法對艙段連接結(jié)構(gòu)進(jìn)行可靠性和靈敏度分析，該方法是通過功能函數(shù)在一些特征點(diǎn)處點(diǎn)處的函數(shù)值來近似計(jì)算功能函數(shù)的低階矩(主要是一階到四階矩)，然后由功能函數(shù)的各階矩來近似失效概率。四階矩可靠性分析方法同其他可靠性分析方法相比，不需求解功能函數(shù)的設(shè)計(jì)點(diǎn)，調(diào)用功能函數(shù)的次數(shù)較少。因此，四階矩法適用于變量不多的復(fù)雜工程結(jié)構(gòu)可靠性分析［6－9］。

可靠性分析的一個(gè)目標(biāo)是確定功能函數(shù)g(x)的失效概率Pf:

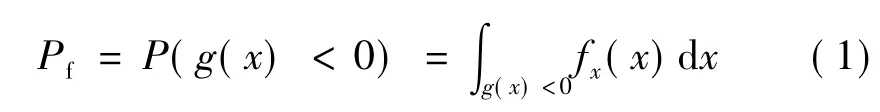
式中 ?x(x)為功能函數(shù)g(x)的聯(lián)合概率密度函數(shù)。

設(shè)x={x1，x2，…，xn}為聯(lián)合概率密度函數(shù)為?x(x)的隨機(jī)變量，則結(jié)構(gòu)響應(yīng)功能函數(shù)g=g(x)=g(x1，x2，…，xn)的概率矩可由下式計(jì)算:

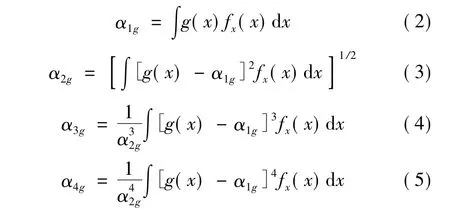
式中 αkg表示結(jié)構(gòu)響應(yīng)的k階無量綱中心矩。

功能函數(shù)的概率矩給出了功能函數(shù)的部分統(tǒng)計(jì)信息，而功能函數(shù)的概率密度函數(shù)是息息相關(guān)，獲得了功能函數(shù)g(x)的概率矩，那么就可非常容易得到失效概率。

失效概率只包含了功能函數(shù)概率密度函數(shù)的部分信息，在得到了功能函數(shù)的概率矩后，一些學(xué)者在合理假設(shè)基礎(chǔ)上，給出了如下一些近似算法。在考慮功能函數(shù)前四階矩來近似失效概率的方法稱為四階矩法，基于四階矩的可靠度指標(biāo)β4M為

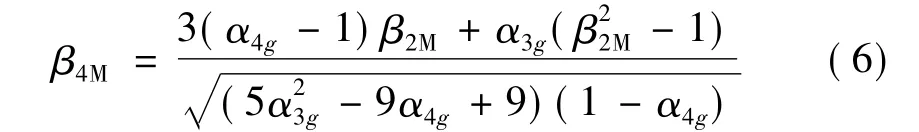
式中 β2M為功能函數(shù)前兩階矩的可靠度指標(biāo)，可近似為

相應(yīng)的考慮前四階矩的失效概率為

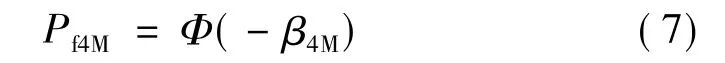
為了提高可靠性分析效率，編譯大量的計(jì)算機(jī)程序，能產(chǎn)生基本變量的均值、標(biāo)準(zhǔn)差、偏度和峰度，實(shí)現(xiàn)有限元結(jié)果自動提取，并計(jì)算功能函數(shù)的均值、標(biāo)準(zhǔn)差、偏度和峰度。由于功能函數(shù)中只有3個(gè)基本變量，四階矩法只需調(diào)用27次功能函數(shù)，就能得到功能函數(shù)的均值、標(biāo)準(zhǔn)差、偏度和峰度分別為α1g=98.30，α2g=49.66，α3g=0.86，α4g=2.44，代入式(6)可得可靠度指標(biāo)為 β4M=3.04，失效概率 Pf4M=1.18 ×10－3。

4 艙段結(jié)構(gòu)可靠性靈敏度分析

可靠性靈敏度一般定義為失效概率Pf對基本變量 x={x1，x2，…，xn}的分布參數(shù) θ(k)xi(i=1，2，…，n，k=1，2，…，mi)的偏導(dǎo)數(shù)，mi為第 i個(gè)變量 xi的分布參數(shù)的總個(gè)數(shù)。根據(jù)前文中所給出的功能函數(shù)矩估計(jì)的失效概率近似公式(7)，由失效概率Pf與可靠度指標(biāo)的關(guān)系，以及可靠度指標(biāo)與極限狀態(tài)函數(shù)各階矩的關(guān)系，可采用函數(shù)求導(dǎo)法推出Pf對基本變量分布參數(shù)的靈敏度計(jì)算公式:

均值靈敏度反映了變量均值大小對可靠度的影響程度［7－8］，其相應(yīng)的計(jì)算公式如式(9)所示:

標(biāo)準(zhǔn)差靈敏度反映了變量參數(shù)波動性對可靠度的影響，其相應(yīng)的計(jì)算公式為式(10)所示。

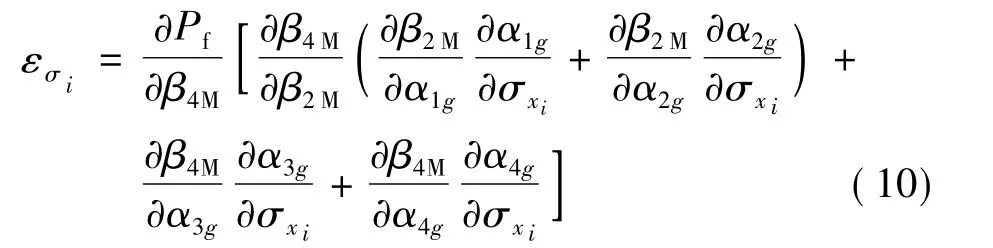
將功能函數(shù)的各階矩對基本變量分布參數(shù)的偏導(dǎo)數(shù)得到后，通過求其數(shù)學(xué)期望就可得到可靠性靈敏度參數(shù)如表3所示。

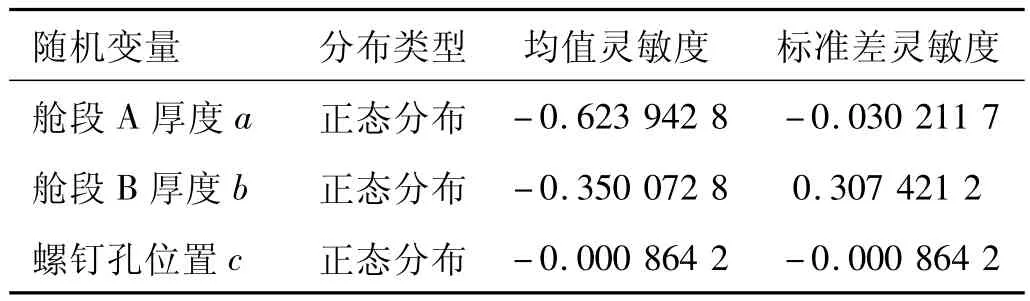
表3 基本變量靈敏度Table 3 Basic parameters sensitivity

從表3可看出，連接段的艙段厚度是影響艙段結(jié)構(gòu)強(qiáng)度的主要因素。因此，在加工制造過程中，應(yīng)嚴(yán)格控制艙段連接段的厚度。

5 結(jié)論

(1)對導(dǎo)彈艙段結(jié)構(gòu)進(jìn)行非線性接觸有限元分析，校核各艙段構(gòu)件均滿足設(shè)計(jì)規(guī)范。

(2)考慮到導(dǎo)彈艙段連接結(jié)構(gòu)關(guān)鍵部件尺寸的隨機(jī)性，將可靠性分析方法與有限元參數(shù)化分析方法相結(jié)合，采用四階矩法對艙段結(jié)構(gòu)可靠性分析，計(jì)算得到艙段結(jié)構(gòu)的失效概率為Pf=1.18×10－3。

(3)對導(dǎo)彈艙段連接結(jié)構(gòu)進(jìn)行靈敏度分析發(fā)現(xiàn)，各艙段連接段的厚度是影響艙段結(jié)構(gòu)強(qiáng)度的主要因素。

［1］徐金中.導(dǎo)彈艙段模擬件在強(qiáng)激光和力學(xué)載荷作用下的屈曲數(shù)值模擬［D］.長沙:國防科技大學(xué)，2003.

［2］相升海，張平等.導(dǎo)彈軌姿控艙體的強(qiáng)度分析［J］.固體火箭技術(shù)，2006，29(5).

［3］馬康民，宜建光，康進(jìn)興.30CrMnSi2A鋼飛機(jī)主梁疲勞斷裂分析［J］.材料工程，2001(10):42-44.

［4］張棟.導(dǎo)致空難的機(jī)翼大梁的疲勞失效分析［J］.材料工程，2001(增刊).

［5］導(dǎo)彈結(jié)構(gòu)·材料·強(qiáng)度［M］.北京:宇航出版社，1996.

［6］宋軍.基于矩方法的可靠性及可靠性靈敏度研究［M］.西安:西北工業(yè)大學(xué)，2007.

［7］高宗戰(zhàn)，劉志群，姜志峰，等.飛機(jī)翼梁結(jié)構(gòu)強(qiáng)度可靠性靈敏度分析［J］.機(jī)械工程學(xué)報(bào)，2010，46(14).

［8］高宗戰(zhàn)，何新黨，姜志峰，等.有機(jī)玻璃邊緣連接結(jié)構(gòu)疲勞壽命可靠性分析［J］.材料工程，2010(5).

［9］張義民，張旭方，楊周，等.多失效模式機(jī)械零部件可靠性靈敏度設(shè)計(jì)［J］.機(jī)械強(qiáng)度，2009，31(6).