考慮腳掌轉動的跳躍機器人動力學與軌跡規劃

胡勝海，徐鵬，鄧坤秀，郭彬

(哈爾濱工程大學機電工程學院，黑龍江哈爾濱150001)

隨著機器人研究領域向地形復雜化、環境非結構化、任務自主化的方向擴展，要求機器人具有更強的自主性、自治性、移動性和地形適應性.在這些新的任務和形勢下，相比輪式或履帶式機器人，腿式跳躍機器人將越發受到重視［1］.最早的跳躍機器人模型是由Raibert等研制的彈性負載倒立擺模型，即SLIP模型［2］，隨后的跳躍機器人的研究大多是基于SLIP模型.眾所周知，SLIP模型假定系統質心位置始終保持在股關節上，而這與自然界中動物關節腿生物學特征不符.近年來，研究者正試圖研制能夠很好地體現動物跳躍運動原理的多關節腿式模型［3-5］.但是這些機器人在建立動力學模型時都很少考慮腳掌的轉動對跳躍運動的影響.

本文研制了一種由旋轉關節組成的單腿平面跳躍機器人.腳掌與地面的柔順關系設計為彈簧-阻尼模型.在存在腳掌轉動的起跳相和落地相，由于足尖與地面的接觸存在被動自由度，機器人模型變為欠驅動的.基于跳躍機器人等價的二連桿模型進行了跳躍運動軌跡規劃，并給出了一個期望軌跡與實際軌跡非線性誤差最小化的曲線方程.

1 機器人結構與跳躍運動序列

雙關節跳躍機器人是一個具有2個主動關節的腿型機器人，如圖1所示.機器人由3個均質連桿組成，分別為腳掌、小腿和大腿.腳掌的自由端為足尖，連接腳掌和小腿的關節是踝關節，連接小腿和大腿的關節是膝關節.每個關節由安裝在連桿中心位置的直流伺服電機通過同步齒形帶驅動.雙關節機器人跳躍運動限制在徑向平面內，因此它是一個平面跳躍機器人.

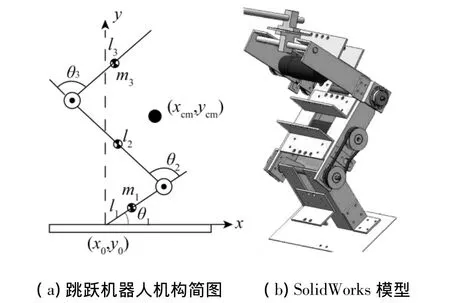
圖1 跳躍機器人機構簡圖和Solidworks模型Fig.1 Hopping robotmodel and Solidworksmodel

建立如圖1所示的慣性坐標系.足尖的初始位置標為(x0，y0)，踝關節和膝關節的笛卡爾坐標為(x1，y1)和(x2，y2).關節坐標向量 θb=(θ2，θ3)T描述了機器人的相對構型.θ1是腳掌與地面之間的絕對夾角.廣義坐標向量 θa=(θ1，θbT)T描述了機器人的絕對構型.每個角度按逆時針為正.腳掌、小腿和大腿的長度和質量分別為li和mi(i=1，2，3).

一個典型的跳躍運動過程包括起跳相、飛行相和落地相.雙關節跳躍機器人的絕對位置是由位于質心的笛卡爾坐標(xCM，yCM)確定的.在起跳相和落地相，機器人的腳連桿與地面接觸，并且CM≠0;在飛行相時機器人與地面不接觸.

2 考慮腳掌轉動的機器人動力學

在生物和人類的跳躍運動過程中，腳掌與地面的相互作用對跳躍性能影響很大，為了模擬這種特性，本文采用如圖2所示的柔順性模型表示雙關節跳躍機器人的腳掌與地面的關系.腳掌與地面的整個接觸表面由安裝在足尖的固定支點和安裝在踝關節處的彈簧-阻尼系統代替.

腳掌柔順性模型作如下假設:

1)整個腳掌與地面的接觸表面由足尖接觸和踝關節接觸代替.

2)足尖與地面的接觸作為一個固定支點，跳躍機器人在這一點上不打滑、彈回和越過等.地面反力的垂直分量為正，水平分量與垂直分量的比值不超過靜摩擦系數［6-8］.

3)踝關節與地面接觸作為一個彈簧-阻尼系統，在這點跳躍機器人能彈回或者透過.

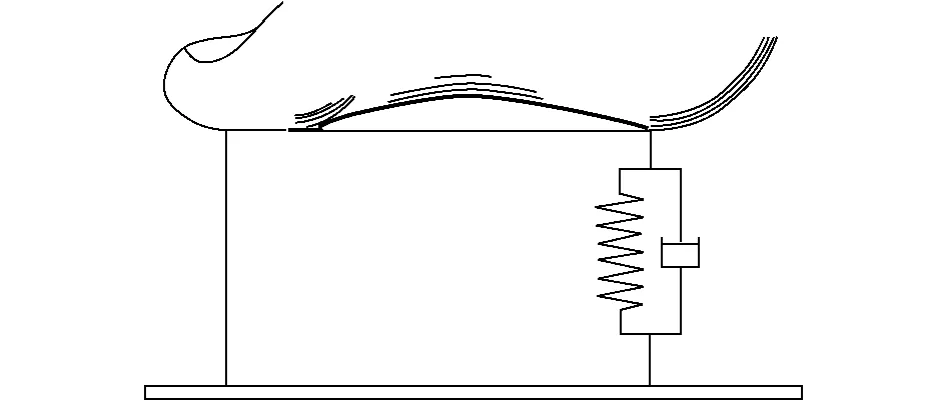
圖2 腳掌柔順性模型Fig.2 Foot compliancemodel

2.1 起跳相和落地相的拉格朗日動力學

在起跳相和落地相，機器人質心的位置［xCM(θa)，yCM(θa)］能通過足尖位置計算出來:

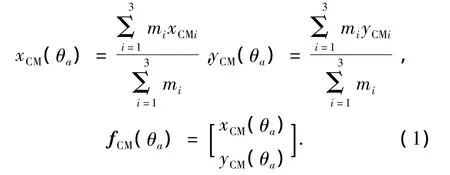
這里，mi和(xCMi，yCMi)為第i個連桿質心的質量和位置.因此，雙關節跳躍機器人質心的線速度為

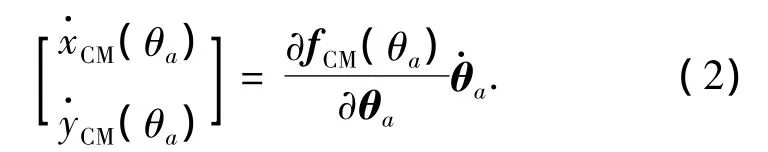
考慮腳掌轉動，忽略各關節摩擦，由拉格朗日方程描述雙關節跳躍機器人動力學模型的起跳相和落地相［9］.機器人動力學模型有如下形式:

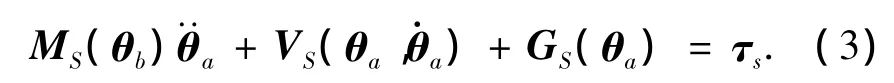
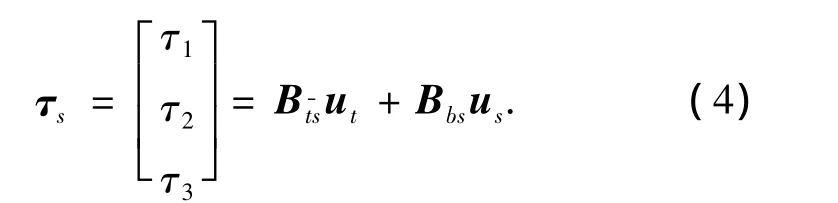
式中:MS是一個關于足尖的3×3慣性矩陣，VS是一個包含哥式力和離心力的3×1向量，GS是一個3×1的重力項.τS是應用到跳躍機器人的廣義力和力矩向量，外力矩為式中:下標s代表起跳相和落地相，b代表關節坐標向量代表足尖地面關節.uS=［τ2τ3］T分別是作用在踝關節和膝關節扭矩.ut=τ1是由作用在踝關節-地面接觸點的豎直方向地面反力在足尖-地面接觸點上產生的扭矩:

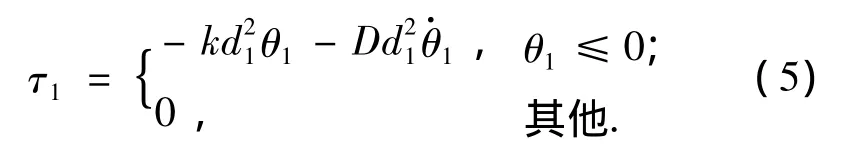
式中:k和D是踝關節-地面接觸的彈簧常數和阻尼系數.式(4)中:

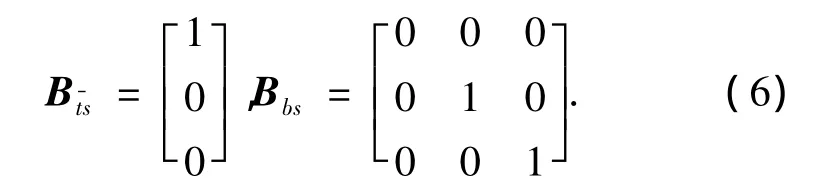
在起跳相和落地相，跳躍機器人必須滿足下面3 個約束條件［10］:

1)作用在機器人足尖處的地面反力的豎直分量大于等于零，即

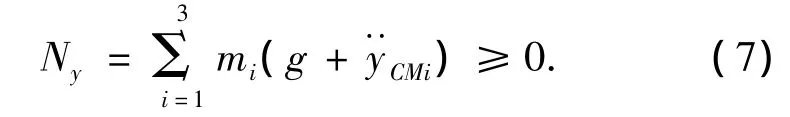
當且僅當在起跳相末時和落地相初始時刻，Ny=0.Ny為地面反力的豎直分量CMi為各個連桿質心加速度的豎直分量，其值可由θi的值求出.

2)各關節的輸入力矩為對稱有限值，即

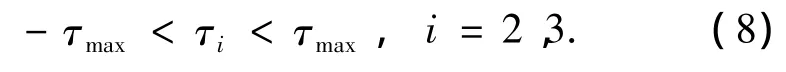
3)碰撞發生在飛行相末時足尖接觸地面時刻.假定碰撞的瞬時過程為一個完全非彈性碰撞過程，即在碰撞后:足尖速度瞬間變為零，關節速度瞬間改變［11］，機器人的姿態保持不變.碰撞之后，足尖-地面接觸當做是理想支點.碰撞前后的位置和速度分別用“-”和“+”標記.利用文獻［11］的模型可得到碰撞后的關節速度為

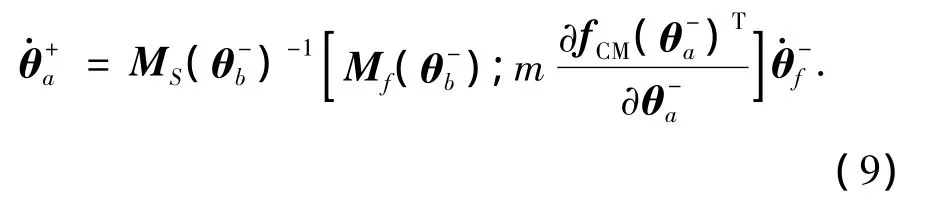
2.2 飛行相的拉格朗日動力學

對于飛行相，廣義坐標向量考慮為 θf=(θ1，θTb，xCM，yCM)T.則飛行相動力學模型為

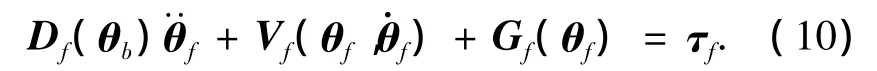
式中:Vf是一個包含科氏力和離心力的5×1向量，Gf是一個5×1的重力項，Df為

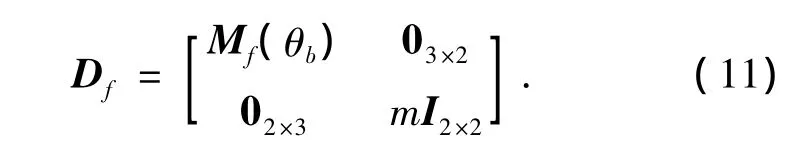
式中:I2×2是2×2單位矩陣，Mf(θb)是關于質心的跳躍機器人慣性矩，可以通過下式［6］求得

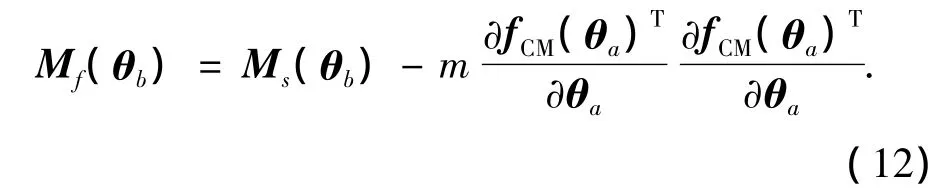
外扭矩為

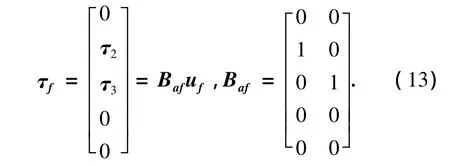
式中:下標 f代表飛行相，a代表絕對姿態.uf=［τ2τ3］T是在飛行相時，分別作用在踝關節和膝關節扭矩.在飛行相，雙關節跳躍機器人的質心按照拋物線軌跡運動，其約束條件為:

1)質心遵守牛頓第二定律，即

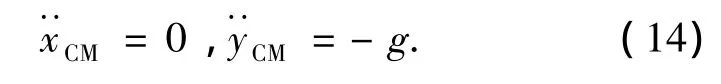
3 軌跡規劃

軌跡規劃過程［12］是基于跳躍機器人二連桿等價模型，如圖3所示.在等價模型中，把腳掌當做一個連桿，踝關節到跳躍機器人剩余連桿質心的距離當做另一個連桿.機器人剩余連桿質心的笛卡爾坐標(xCM0(θb)，yCM0(θb))是建立在腳掌坐標系(Xf，Yf)上的.考慮跳躍機器人的機械結構，關節坐標向量 θb的合理范圍為 -1.571 ≤ θ2≤ 1.047，-2.094≤θ3≤2.618.

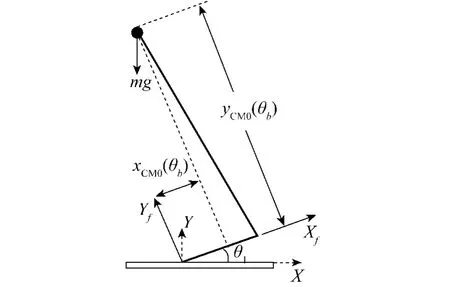
圖3 包含腳掌的跳躍機器人二連桿等價模型Fig.3 Two-link equivalentmodel of the hopping robot

3.1 起跳相軌跡規劃

在起跳相，(xdCM0(t)，ydCM0(t))采用以下形式:

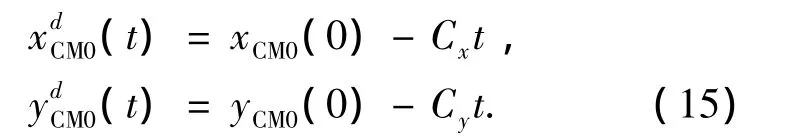
3.2 飛行相軌跡規劃

在飛行相機器人的質心按照式(14)運動.關節坐標向量θb改變基于足尖坐標(x0，y0)的機器人質心位置.豎直方向期望軌跡ydCM0(t)為

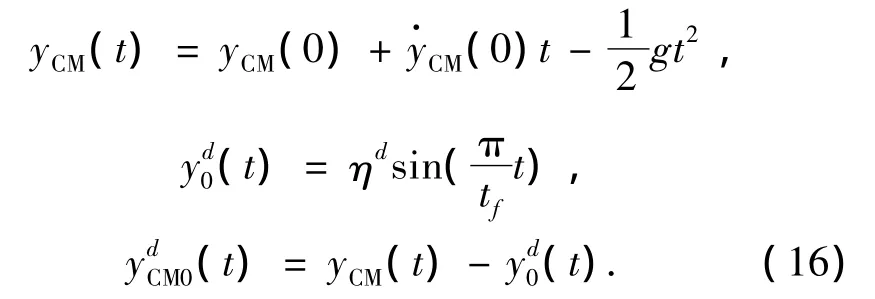
式中:ηd是期望的跳躍高度，tf為期望的跳躍時間，yd0(t)是y0的期望軌跡，如圖4所示.同樣，水平方向期望軌跡xdCM0(t)為式中:δd為期望的單位跳躍遠度，xd0(t)是x0的期望軌跡，如圖4所示.xCM(0)、CM(0)、yCM和CM(0)是起跳相末時的值.ηd、δd和tf的選取要滿足在飛行相末時 θ1＞0.

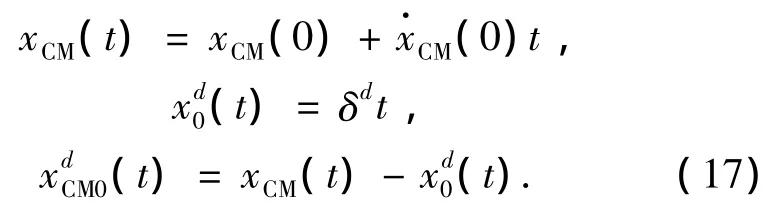
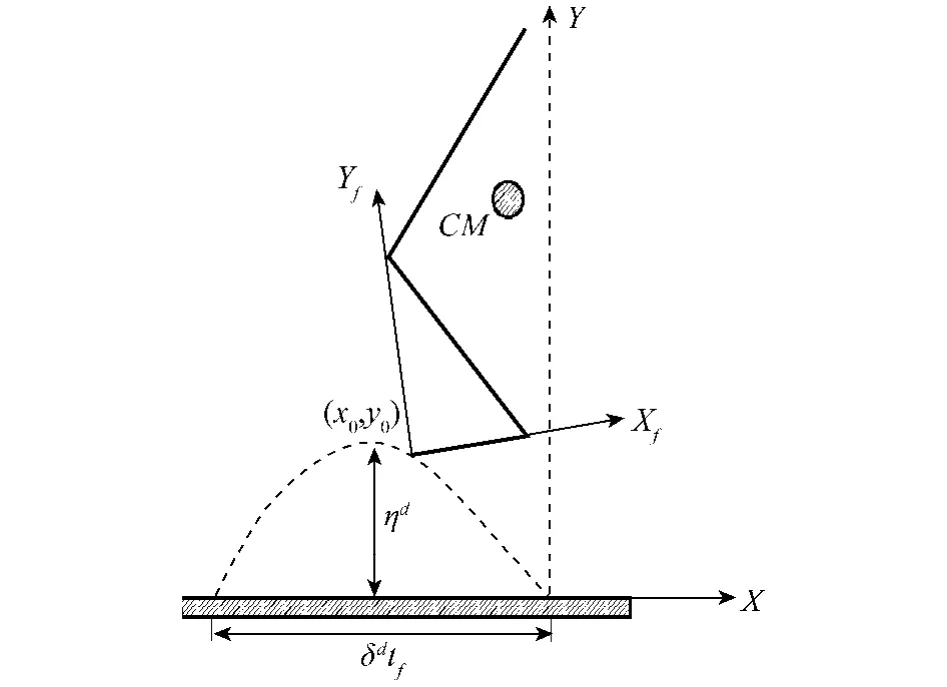
圖4 飛行相期望軌跡Fig.4 Desired trajectory of flight phase

3.3 落地相軌跡規劃

落地相的初始位置是飛行相的末時位置，同時由于在飛行相末時發生碰撞，由式(9)知，落地相的初始速度瞬時改變.落地相期望的形位變量θdj(t)(j=2，3，4)為常數，且滿足:

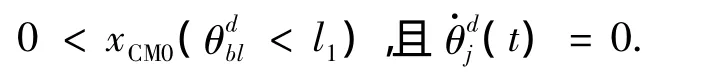
4 仿真與實驗

4.1 仿真

綜合式(15)～(17)，可得如下結論:跳躍運動的軌跡是由不同階段期望運動軌跡θb和θ·b相互耦合確定的.而這些參數的選擇又是由 Cx、Cy、ηd、δd和tf間接決定的，且必須滿足跳躍運動軌跡約束條件(7)、(8)、(9)、(14)等.在本文中選擇跳躍運動過程中期望運動軌跡參數誤差最小化作為優化方程，即

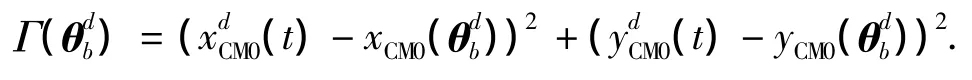
采用MATLAB＇s LSQNONLIN函數求得期望步態θdb(t).滿足上式非線性誤差最小化原則求得的θdb位于跳躍機器人合理的形位參數范圍內，采用形如四階多項式函數描述的θdj(t)，即)，期望運動過程中的誤差精度能達到10-4m.

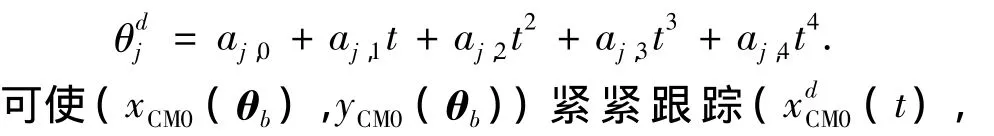
在仿真計算中，與機器人有關的參數為:l1=0.19 m，l2=0.15 m，l3=0.14 m，m1=600 g，m2=800 g，m3=750 g，關節最大約束轉矩τmax=80 N·m踝關節-地面接觸的彈簧常數k=4 000和阻尼系數D=0.8.仿真結果所得到的非線性誤差最小化的運動軌跡是由如下參數值所決定:Cx=1.5 m/s，Cy=2 m/s，ηd=0.25 m，δd=1.8 m/s 和 tf=250 ms.在此參數下的踝關節和膝關節的跳躍過程運動軌跡如圖5所示.

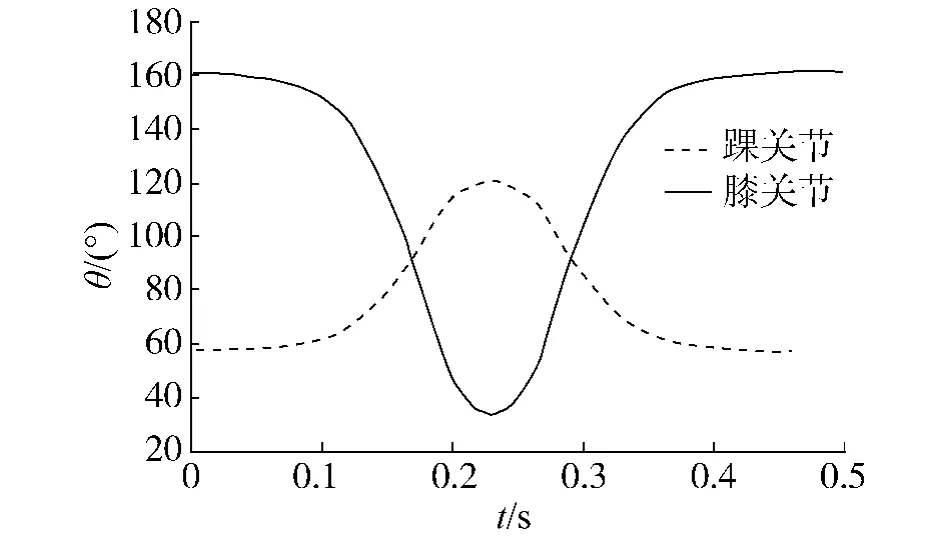
圖5 關節運動軌跡Fig.5 Jointmotion trajectory

仿真過程中的踝關節扭矩和膝關節扭矩如圖6所示.仿真中，踝關節扭矩最大值為76.48 N·m，膝關節扭矩最大值為-52.64 N·m，且膝關節扭矩的最大值在踝關節扭矩最大值之后出現.仿真結果說明了踝關節扭矩對跳躍性能影響較大.

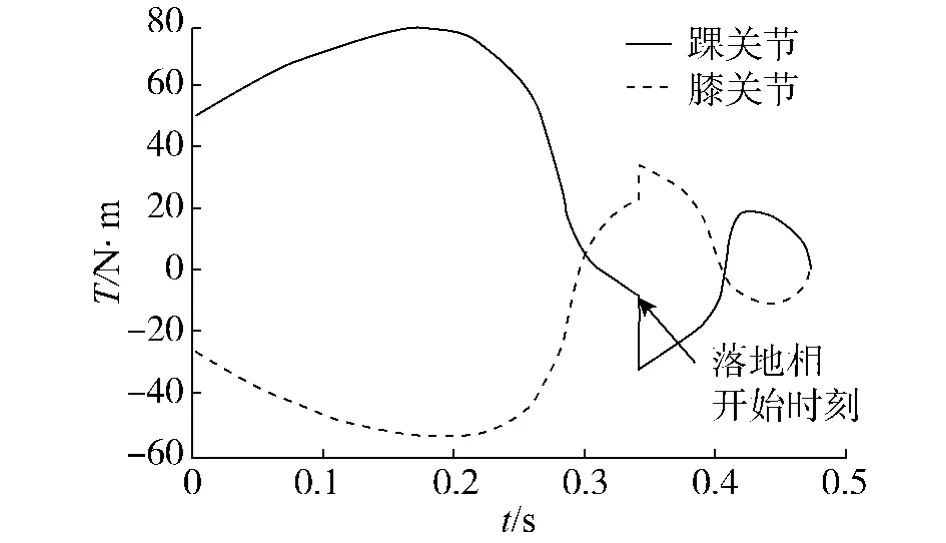
圖6 最佳軌跡的關節力矩Fig.6 Joint torques of optimumtrajectory

在t=0.33 s時，跳躍運動進入落地相.此時，踝關節扭矩和膝關節扭矩發生瞬間改變，導致踝關節和膝關節的速度和加速度在此刻都發生瞬間變化.

跳躍仿真過程中，足尖與地面的絕對角度θ1及被動扭矩τ1的變化曲線如圖7所示.在仿真剛開始時，由于主動關節電機扭矩的作用，機器人對地面有沖擊作用力，在足尖處產生被動扭矩τ1，其最大值為64 N·m.這個被動扭矩對機器人的跳躍起積極作用，在仿真中希望其值越大越好.在t=0.03 s時，機器人腳掌開始發生轉動.t=0.33 s落地相發生后，由于落地沖擊，使θ1＜0，在足尖處產生被動扭矩τ1，其最大值為106.5 N·m.這個被動扭矩造成機器人的落地姿態不穩定，在仿真中希望其值越小越好.

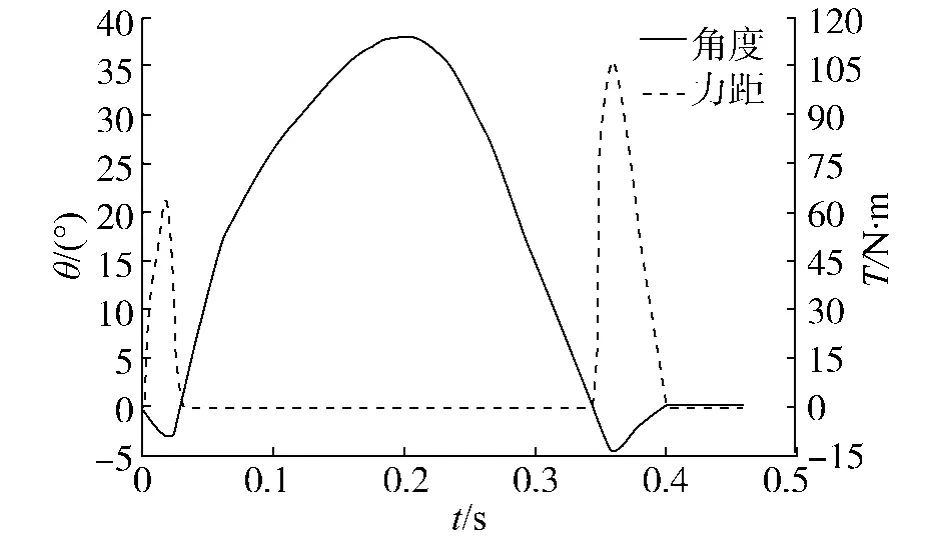
圖7 腳掌與地面的角度及扭矩Fig.7 Joint angle and torques between foot and ground

4.2 樣機實驗

雙關節平面跳躍機器人的機械結構用鋁板連接.該跳躍機器人的驅動電機型號是CBL3570A，其技術參數如下:額定電壓為 18 V，額定轉速為7 500 r/min，額定功率為60 W.配套編碼器為1000線，減速比為19.該系統采用DSP進行控制，主控芯片是TI公司的TMS320F2812.機器人跳躍實驗是在一層橡膠墊上進行的.橡膠墊能防止單腿跳躍機器人起跳時打滑，并在機器人落地時提供阻尼器吸收落地沖擊能量.為了增加直流伺服電機的爆發性，在機器人踝關節和膝關節處增加拉簧，所以跳躍實驗比仿真所需時間少.圖8為一組跳躍運動過程的圖片.實驗測得，當 θ1=30°～35°時，機器人離地，此時跳躍機器人能獲得最大跳躍高度為0.15～0.20 m，跳躍距離為0.25 ～0.28 m.

圖8 一組跳躍運動圖片Fig.8 A groupof hopping motion

5 結束語

本文針對雙關節跳躍機器人模型，考慮腳掌對跳躍運動的影響，采用拉格朗日方法建立機器人在支撐相和飛行相的動力學模型.以期望運動軌跡參數誤差最小化為目標，基于機器人二連桿等價模型，采用四階多項式規劃了機器人跳躍運動步態.仿真和樣機實驗結果為機器人的系統優化和運動控制提供了重要依據.同時，本文研究結果對解決如腿式跳躍機器人這類混雜非線性欠驅動系統的動力學與軌跡規劃問題具有指導意義.

［1］徐兆紅.腿式跳躍機器人運動規劃與穩定性恢復研究［D］.上海:上海交通大學，2009:2-16.XU Zhaohong.Study onmotion planning and stability recovery for legged jumping robot［D］.Shanghai:Shanghai Jiao Tong University，2009:2-16.

［2］RAIBERTmH.Legged robots that balance［M］.Cambridge，MIT Press，1986:26-45.

［3］ZEGLIN G J.Uniroo:a one legged dynamic hopping robot［D］.Cambridge:Massachusetts Institute of Technology，1991:78-93.

［4］HYON SH，MITA T.Development of a biologically inspired hopping robot Kenken［J］.IEEE International Conference on Robotics and Automation，2002:3984-3991.

［5］SUNG S，YOUmY.Landing motion control of articulated legged robot［J］.IEEE International Conference on Robotics and Automation，2007:3230-3236.

［6］CHEVALLEREAU C，WESTERVELT E R，GRIZZLE J W.Asymptotically stable running for a five-link，four-actuator，planar bipedal robot［J］.Int JRobot，2005，24(6):431-464.

［7］WESTERVELT E R，GRIZZLE JW，KODITSCHEK D E.Hybrid zero dynamics of planar biped walkers［J］.IEEE Trans AutomControl，2003，48(1):42-56.

［8］WESTERVELT E R，GRIZZLE JwC.CHEVALLEREAU C.Feedback control of dynamic bipedal robot locomotion［J］.Boca Raton，FL:CRC.2007，43(4):142-153.

［9］SPONG mW，VIDYASAGAR M.Robot dynamic and control［M］.NewYork:Wiley，1989:56-89.

［10］楊煜普，耿濤，郭毓.一種新型翻轉跳躍運動機器人的運動結構與軌跡規劃［J］.上海交通大學學報，2007，37(7):1110-1113.YANG Yupu，GENG Tao，GUO Yu.Structure and trajectory planning of a novel flipping robot［J］.Journal of Shanghai Jiao Tong University，2007，37(7):1110-1113.

［11］HURMUZLU Y，MARGHITU D B.Rigid body collisions of planar kinematic chains with multiple contact points［J］.Int JRobot，1994，13(1):82-92.

［12］李東潔，邱江艷，尤波.一種機器人軌跡規劃的優化算法［J］.電機與控制學報，2009，13(1):123-127.LIDongjie，QIU Jiangyan，YOU Bo.Optimal algorithmfor trajectory planning of the robot［J］.Electric Machines and Control，2009，13(1):123-127.