基于支持向量機的汽車曲軸質量診斷模型

趙 凱，何 楨，何曙光，趙永滿

（天津大學 管理與經濟學部，天津 300072）

0 引言

多元質量控制的概念最早是由Hotelling于1947年提出的。多元質量控制與一元質量控制類似，一般都要求質量特性服從正態分布，多元質量控制是基于多元正態分布建立檢驗統計量進行質量控制的。多元統計過程控制(MSPC)是多元質量控制常用的方法，它通過監控生產過程中多個相關變量，以探測過程可能發生的異常，達到提高產品質量的目的。當前MSPC技術應用中存在的主要問題是，隨著過程變量維數的增加，監控系統的復雜性急劇增加，而變量間的多重共線性又給過程的異常診斷帶來了困難。由于多元過程質量特性之間存在相關性，上述多元質量控制方法難以確定過程變異的來源，即當控制圖報警時，如何判定變異是哪一個或哪幾個質量特性的變動引起的。為了克服存在的這些問題，R.S.Guh[1](2007),Niaki et al.[2](2005)，Hou et al.[3](2003),Yu( 2008;2009)[4;5],Venkat(2003)[6]等學者對該問題應用不同的方法進行了研究。本文將根據某企業汽車曲軸實際生產情況，應用基于支持向量機(SVM)的多元質量控制與診斷方法，結合企業現有MARPOSS綜合測量機的測量數據，對產品的數據進行分析、處理、監測與診斷。

1 T2控制圖

設某多元過程有p個關鍵質量特性，表示為X=(X1,X2,…，Xp)，設每個樣本的樣本容量為n，共有m樣本。進一步假設X服從多元正態分布，即X～Np(μ0,∑0)，其中μ0和∑0分別為總體均值和方差-協方差矩陣。則Xij=(Xij1,Xij2,，…，Xijp)是p維向量，代表在第i個樣本中第j個觀測值的p維質量特性，其中i=1,2,…,m；j=1,2,…,n。Xij的第l成分Xijl表示第l個質量特性，其中l=1,2,…,p。假設Xij是相互獨立且服從在過程受控狀態下均值μ和協方差矩陣∑已知的多元正態分布。一般在實際生產過程中，總體均值μ和方差協方差矩陣∑是未知的，需要從過程受控時采集的初始樣本中分析得到，用估計的樣本均值向量和樣本-協方差矩陣S代替μ和∑。樣本均值向量為樣本方差-協方差矩陣為：

則T2統計量定義為：

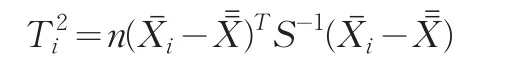
為第i個樣本的均值向量，(?)T為轉置操作。控制限為：

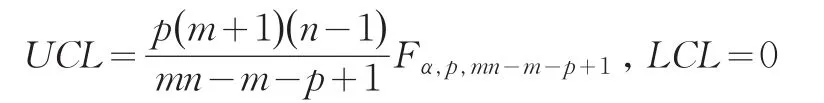
與一元控制圖不同，多元控制圖不但需要設計合理的統計量和控制限，而且在控制圖報警后需要進一步識別導致控制圖報警的變量/變量組合，即多元過程控制圖的異常識別或診斷。

2 支持向量機原理

SVM是一種機器學習算法，其理論基礎是Vapnik等提出的統計學習理論[8]。SVM是將原訓練數據映射到較高的維，在該新的維上，搜索線性最佳分離超平面。對于二分類問題，設訓練樣本集D為(X1,y1)，(X2,y2)，…，(Xi,yi)，其中i=1,2,…,l，l為訓練樣本數，Xi∈Rd為輸入向量，yi∈{ }

+1,-1為輸出分類標志。對于線性可分問題，可以用n維空間中的超平面WXT+b=0將訓練樣本集分開，其中W'=(w1,w2,…,wd)為d維向量且‖ ‖W=1，該平面稱為分類超平面。顯然對于訓練樣本集D，該分類超平面并不唯一，即存在一組與該超平面平行的超平面，均可以將訓練樣本集正確分開，把距離最大的兩個超平面之間的距離稱為分類間隔，則有：

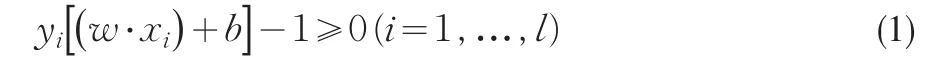
此時最大邊緣等于2‖W‖ ，是分類間隔最大等價于使‖W‖2最小。滿足條件(1)并使‖W‖22最小的超平面稱為最優分類超平面，相距最遠的兩個超平面上的點就稱為支持向量。將該問題轉化為其對偶問題，并采用Lagrange優化方法，得到的優化問題如(2)所示。

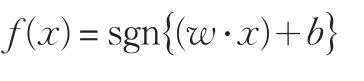
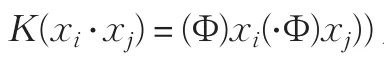
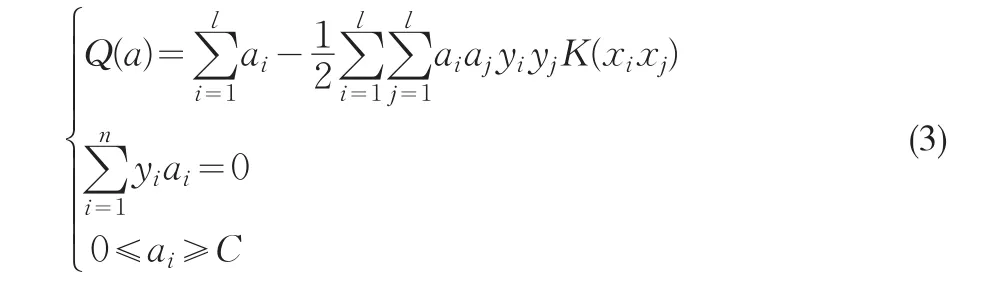
不同的核函數形式對應不同的算法，多項式核函數、高斯徑向基核函數、B樣條核函數等是最常用的核函數，其中高斯徑向基核函數由于具有較強的非線性分類能力而得到廣泛應用，其形式為：

其中，h2是核函數參數。

3 基于SVM的MSPC診斷模型

根據文獻[7]基于SVM的MSPC診斷過程主要包括三個部分：MSPC過程，采用多元控制圖，對制造過程中的多元質量特性進行監控；診斷模型訓練，采用多元過程中的異常數據作為訓練數據集，包括異常質量數據和對應的異常類別，其中異常類別根據導致報警的異常變量/變量組合進行編碼；MSPC診斷，在所構建的診斷模型基礎上，如果MSPC報警，則對過程進行診斷，以確定導致過程異常的變量/變量組合。

針對汽車曲軸生產過程實際問題，考慮加工過程的三個變量，即p=3，筆者構建診斷模型的過程為：

(1)明確過程輸出特性及過程輸出特性的具體要求，抽取生產過程曲軸的樣本，利用多元過程控制圖判明過程是否處于統計受控狀態；通過構造伽馬圖，從圖形的特征接受本文研究的曲軸生產過程的多元正態性；

(2)明確過程處于受控狀態以及過程具有多元正態分布，計算多元過程能力指數，描述過程的能力；

(3)通過生產線MARPOSS綜合測量機中獲取的數據，計算樣本均值向量Xˉ和樣本方差-協方差矩陣S，用Xˉ和S估計總體的均值μ和協方差矩陣Σ；

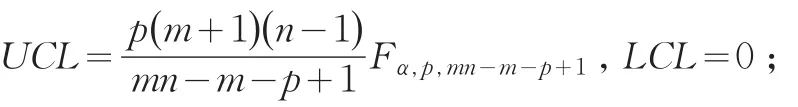
(5)用構建的T2控制圖收集用于構建SVM模型訓練和測試樣本，根據生產的實際情況，對于每一種給定的均值偏移模式，產生50個超出T2控制限的曲軸生產數據，同時產生各不同模式的50個不超出T2控制限的曲軸生產數據；

(6)構建SVM模型。多元過程監控與診斷中，神經網絡等方法在解決診斷問題時，是應用ANN相關模型擬合過程質量特性和變量偏移類別的分類模型，而隨著問題維度的增加，分類的難度顯著增加[7]。而SVM的理論基礎是Vapnik等提出的統計學習理論，統計學習理論采用結構風險最小化原則，提高了模型的泛化能力，且得到的是全局最優解，可有效避免神經網絡中的過學習問題，尤其適合于小樣本學習問題。隨著維度的增加，則異常組合數呈指數增長，如果用單一診斷模型，模型的輸出維度太高，從而給模型的構建帶來了很大的難度[7]。

本文建立的模型如圖1所示，用上面產生的汽車曲軸加工過程中的數據，對模型進行訓練。在MSPC診斷過程中，作者研究的變量p=3，每一個變量分為正常和異常兩種情況，共有8種組合，其中包含受控狀態1種和過程發生偏移的7種。在模型中，過程的每一變量分別應用一個SVM分類模型對各個變量是否存在均值偏移進行診斷，每個SVM分類器的輸出為0或1，其中1代表該變量未發生均值偏移，0代表該變量均值發生偏移。在模型中，將所有3個變量均作為模型的輸入。由于在對每一個變量的偏移進行診斷時，同時考慮了其他變量對該變量的影響，因此并不會忽略變量之間的相關性，而模型個數僅與過程質量特性個數相等；

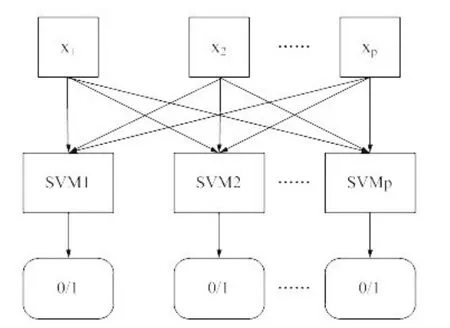
圖1 MSPC均值偏移診斷模型

(7)SVM模型的參數優化。SVM模型訓練過程中，筆者選擇高斯徑向基函數作為SVM的核函數。通過仿真方法對模型的性能進行分析，確定在SVM模型中式(3)和式(4)中的懲罰參數C和核函數參數h2取值；

(8)具體應用。采用T2控制圖進行監控，監控多元加工過程是否有報警；若出現報警點，則利用建立的SVM模型對報警信號進行診斷，判斷均值偏移變量的組合模式，并解釋其實際意義，從而實現多元過程均值偏移模式的診斷。

4 實例

筆者通過對某企業汽車曲軸生產的數據分析來加以說明SVM模型的應用。通常曲軸由多個主軸頸和多個連桿軸頸組成，用于描述曲軸質量的參數較多，包括主軸頸與連桿軸頸的軸徑、圓度、圓柱度以及跳動度、沖程等。其中軸頸的直徑與曲軸的沖程對整個曲軸性能有著關鍵性的作用，其中需要對曲軸的這三個質量特性進行控制，以滿足產品的性能要求。本文選用某型號曲軸終檢數據進行了實例研究，數據包括曲軸主軸頸直徑X1、曲軸連桿軸徑X2及該主軸頸與連桿軸徑構成的曲軸的沖程X3。考慮到生產線的小時生產量、生產線的調整周期及穩定受控狀態等，確定數據抽樣方案。產生過程受控狀態下的樣本50個，過程均值發生偏移的樣本350個，按比例作為模型訓練和測試過程中的訓練樣本和測試樣本。

通過MARPOSS綜合測量機中大量的樣本數據，計算過程受控時的樣本均值向量Xˉ和樣本方差-協方差矩陣S為：

這里假定生產過程中曲軸加工過程的樣本方差-協方差矩陣S保持不變。

SVM模型訓練過程中，選擇的高斯徑向基函數作為SVM的核函數。經過仿真優化得到在SVM模型中重要的參數，懲罰參數C=1200和核函數參數h2=2.9。

表1 SVM模型分類結果

應用所選擇的參數，運用建立的SVM模型采集的數據進行處理，結果見表1。在所有7種變異模式中，其中有一個變量均值發生偏移時，分類的正確率最大為78%以上，三個變量均發生偏移時，分類的正確率為70%，該方法的總變異識別正確率為76%。將該結果與實際生產過程中的MARPOSS綜合測量機相結合，能更好地解決生產現場中遇到的實際問題，為企業產品加工過程起到一定的指導和參考作用。

5 結論

目前，生產加工過程中需要同時控制多個變量，以使質量達到顧客的要求，由于多元過程質量特性之間存在相關性，從而給多元過程質量診斷帶來的困難。本文根據對某企業汽車曲軸加工過程的調研，選取對其產品影響重要的幾個質量特性，應用基于支持向量機的方法模型對產品質量特性的均值偏移情況進行了初步的應用研究，均值偏移只取了正常和便宜兩種情況。通過實例表明，應用了基于SVM的多元質量控制與診斷方法，可以較好地識別多元加工過程中的均值偏移問題，在一定程度上解決了多重線性相關給異常診斷帶來的困難，是對現有曲軸生產線MARPOSS綜合測量機的一個補充應用研究。

[1]Guh,R.S.On-line Identification and Quantification of Mean Shifts in Bivariate Processes Using a Neural Network-based Approach[J].Quality and Reliability Engineering International,2007,（23）.

[2]Niaki,S.T.A,Abbasi,B.Fault Diagnosis in Multivariate Control Charts Using Artificial Neural Networks[J].Quality and Reliability Engineering International,2005,(21).

[3]Hou,T.H.,Liu,W.L.LIN,L.Intelligent Remote Monitoring and Diagnosis of Manufacturing Processes Using An Integrated Approach of Neural Networks And Rough Sets[J].Journal of Intelligent Manufacturing,2003,(14).

[4]Yu,J.B.,Xi,L.F.,Zhou,X.Intelligent Monitoring And Diagnosis of Manufacturing Processes Using An Integrated Approach of KBANN And GA[J].Computer in Industry,2008，(59).

[5]Yu,J.B.,Xi,L.F.A Neural Network Ensemble-Based Model For On-Line Monitoring And Diagnosis of Out-Of-Control Signals in Multivariate Manufacturing Processes[J].Experts Systems with Applications,2009，36(1).

[6]Venkat Venkatasubramanian,R.R.Surya N Kavuri,Kewen Yin.A Review of Process Fault Detection And Diagnosis Part III:Process History Based Methods[J].Computers And Chemical Engineering,2003，(27).

[7]Vapnik V.N.The Nature of Statistical Learning Theory[M].New York:Springer,l 995.

[8]Cristianini,N.,J.Shawe-Taylor.支持向量機導論[M].李國正，王猛，曾華軍譯.北京：電子工業出版社，2007.