矩形截面高層建筑氣動基底扭矩系數均方根值研究

顧 明，張正維，2，全 涌，熊 勇

(1.同濟大學 土木工程防災國家重點實驗室，上海 200092;2.南通大學 建筑工程學院，江蘇 南通 226019)

在高層建筑抗風研究中，通常將風荷載分為順風向、橫風向和扭轉方向三個分量，相對而言，人們對高層建筑扭轉方向風荷載的了解程度遠不及順風向風荷載與橫風向風荷載。如果高層建筑結構的厚寬比較大，或結構不對稱或結構的扭轉自振頻率接近平動自振頻率，風致扭轉效應將成為結構設計不可忽略的一部分;同時高層建筑的扭轉振動能加劇截面邊沿的位移和加速度，且居住者對房屋的扭矩運動特別敏感，因此高層建筑的扭轉風振響應應該引起設計者的重視［1，11]。扭轉向風致響應研究的一般方法是:首先通過風洞試驗得到氣動扭矩，然后根據隨機振動理論得到結構的扭轉風致響應，最后給出工程師進行結構設計所需要的扭轉向等效靜力風荷載［1]。在計算扭轉風振響應的過程中，一般將扭轉風振響應分為背景分量與共振分量來計算，計算背景響應時需要氣動基底扭矩系數均方根值，計算共振響應時需要氣動基底扭矩系數的功率譜。由于篇幅的限制，本文只對氣動基底扭矩系數均方根值進行研究，其功率譜將在專門的文章進行介紹。

從20世紀90年代起，對結構風致扭轉響應的研究逐漸增多，取得了一些比較有意義的成果，表1給出了矩形截面高層建筑基底扭矩系數均方根值的國內外研究成果。國內外的主要研究如下:

Marukawa［2，5]通過高頻測力天平試驗給出了基底扭矩系數均方根值的計算公式，并且考慮了風場的影響。Liang［9]通過測壓試驗擬合得到了基底扭矩系數均方根值，但是該值是分層疊加得到，其中選用的無量綱風速為每層測點高度處的風速，而不是通用的選擇頂部高度處的風速。AIJ［7]給出了基底扭矩系數均方根值的計算公式，但是沒有考慮長細比與風場的影響。唐意［11]采用剛性模型測壓試驗給出了層扭矩系數均方根值的計算公式，考慮了厚寬比與風場的影響。Ha［10]通過高頻測力天平試驗給出了基底扭矩系數均方根值的計算公式，沒有考慮長細比與風場的影響。

Choi［3]，Yutaka［6]，以及 Zhou［8]也對矩形截面高層建筑基底扭矩系數均方根值進行了研究，但是沒有給出相應的擬合公式。

本研究在風洞中采用高頻測力天平進行了4類不同風場71個典型建筑模型的風洞試驗，對高層建筑基底扭矩系數均方根值進行了細致、全面的研究，考察了截面厚寬比、模型長細比和風場對基底扭矩系數均方根值的影響，擬合得到了基底扭矩系數均方根值的經驗公式，通過與國內外研究成果的比較，對擬合公式的可使用性進行了評估，為高層建筑的結構設計及相關荷載規范的制定和修改提供了很好的參考。

1 風洞試驗概況

1.1 試驗設備及模型概況

本試驗在同濟大學土木工程防災國家重點試驗TJ－1大氣邊界層風洞中進行，風洞試驗段高1.8 m，寬1.8 m，長18 m，風速范圍為1 m/s－30 m/s，連續可調。試驗模型由50 mm×50 mm，厚度為1mm的鋁棒為芯棒來提供剛度，外部采用泡沫塑料試驗建筑不同外形的模擬，從而使模型質量小而剛度大，以確保天平－模型系統有足夠高的固有頻率。試驗所采用天平基底彎矩與扭矩的量程為30 Nm，測量精度為0.004 Nm，測量精度很高。試驗的采樣頻率為600 Hz，采樣時間為60 s。

表1 基底扭矩系數均方根值研究成果Tab.1 Research results of RMSvalues of base torsional moment coefficient

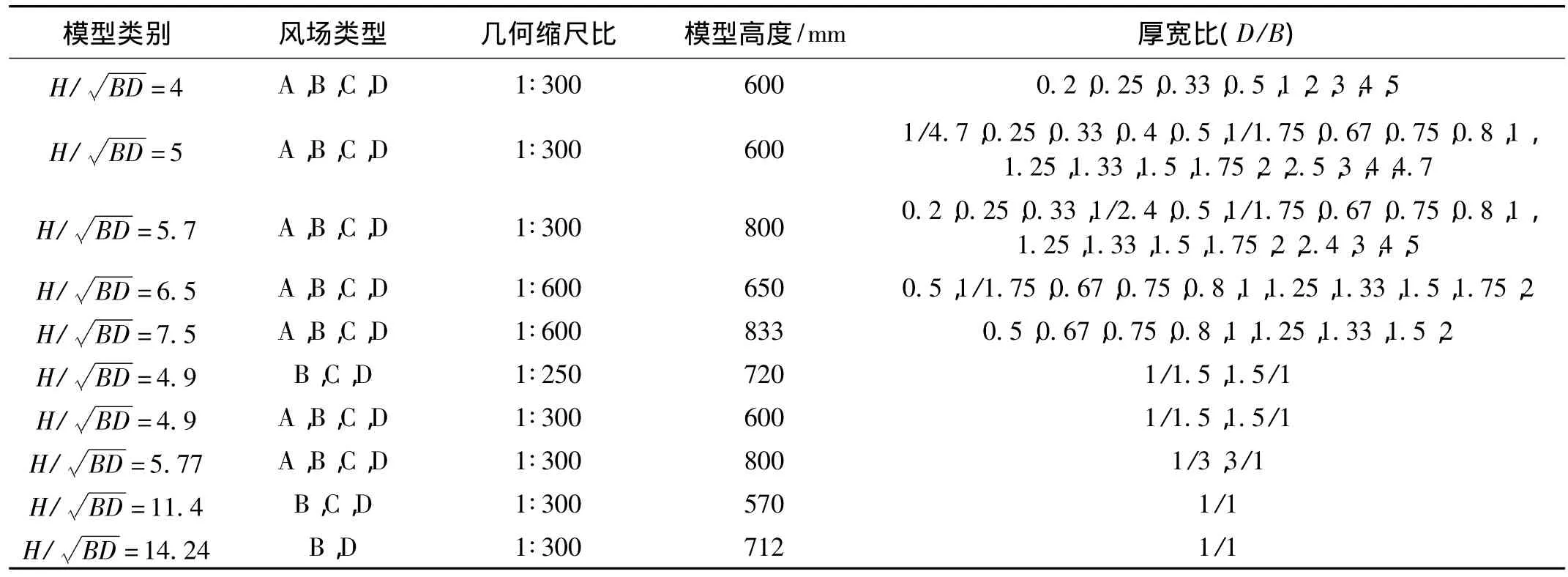
表2 試驗模型參數Tab.2 Parameters of experiment models

1.2 試驗數據處理

利用高頻天平測力技術在風洞中對建筑模型的氣動力進行測量時，要求天平模型系統具有較高的頻率。本課題試驗中所有天平模型系統的一階振型中扭轉向的固有頻率都大于130 Hz，遠遠高于風荷載譜密度的頻率范圍，模型自身的振動引起的模型荷載測量上的誤差就可以忽略不計。對于基底扭矩譜無需像橫風向與順風向基底彎矩譜一樣進行修正以減小天平模型系統頻率不夠高而對風荷載譜產生的放大作用。

本文無量綱的氣動力系數定義如式(1)所示:

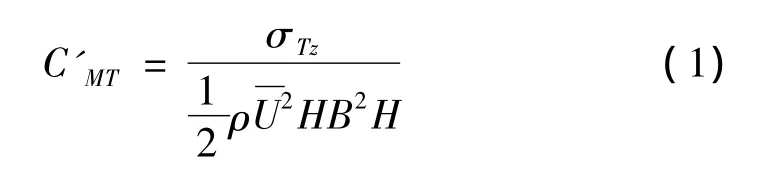
其中，C'MT為基底扭矩系數均方根值，為頂部來流風壓，B為建筑的迎風面寬度(特征寬度)，H為建筑的迎風面高度，σTz為基底扭矩的均方根。

1.3 試驗結果合理性驗證

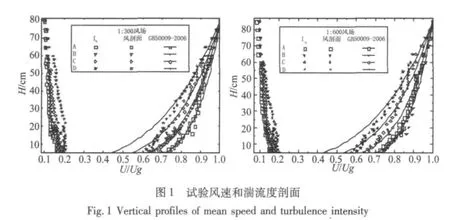
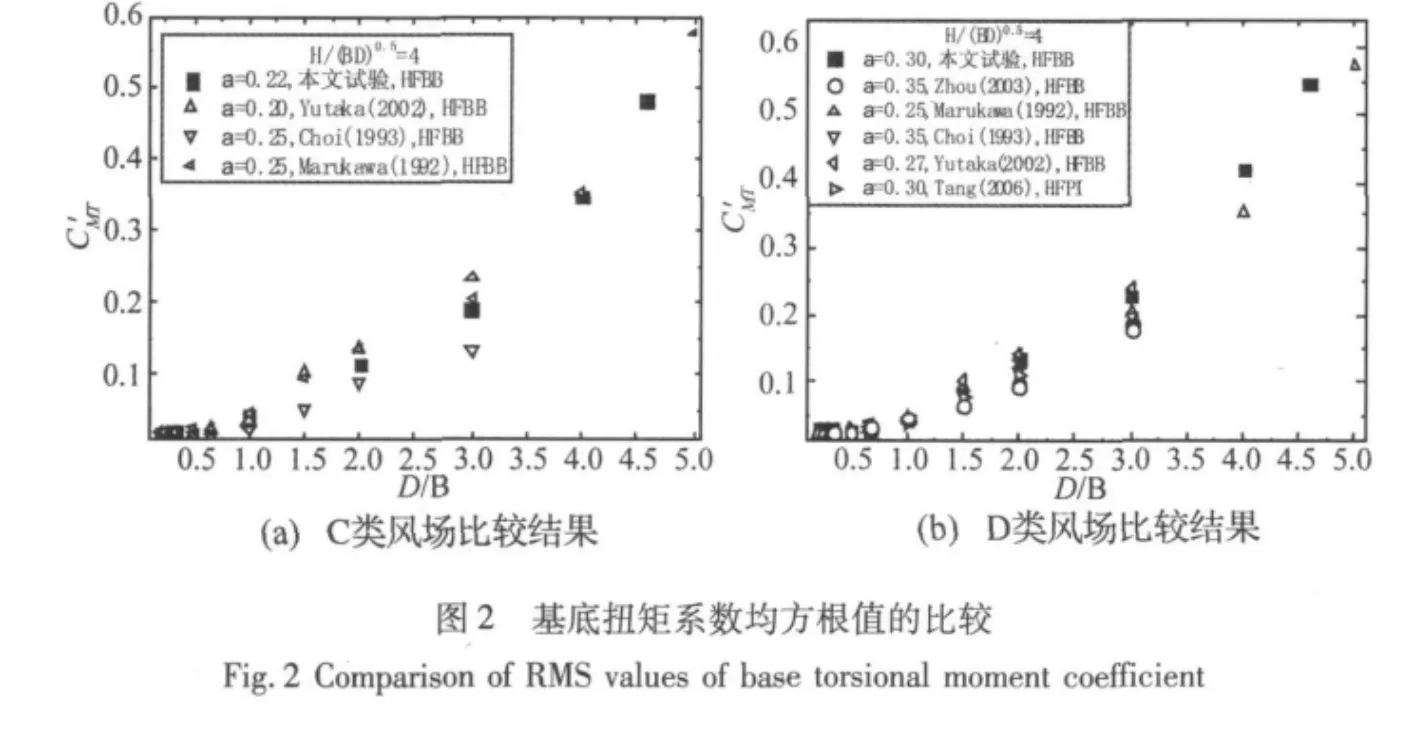
為了驗證本試驗結果的合理性，圖2給出了本文結果與國內外主要成果的比較。從圖中可以看出，在C類情況下，各種試驗的湍流強度以及分剖面指數比較接近，本文的試驗結果與國內外主要研究成果有很好的一致性;在D類風場下，在厚寬比D/B＞2的情況下，本文的試驗結果比Marukawa［2]的試驗結果偏大，主要是由于本文D風場的湍流度比 Marukawa［2]的湍流度偏大，研究表明:當厚寬比D/B＞2后，扭轉氣動力的主要受紊流強度與重附著流的影響，增大紊流度能顯能夠使重附著流提前發生，從而使基底扭矩系數均方根值變大。本文試驗結果與前人的大量試驗具有很好的一致性，從而說明本文的試驗方法以及數據處理方法是合理可行的。

2 試驗結果

圖3～圖5給出了所有71個不同模型在A，B，C，D四類風場中0°與90°風向角下基底扭矩系數均方根值隨厚寬比、長細比與風場類型的變化規律。

2.1 厚寬比的影響

圖3給出厚寬比對基底扭矩系數均方根值的影響。從圖中可以看出，在一定長細比與風場類型下，基底扭矩系數均方根值隨D/B的增大而單調增加。當模型厚寬比D/B＜1時，基底扭矩系數均方根值隨著厚寬比的增大而增大，但是增大幅度不大，這主要是由于當厚寬比D/B＜1時，扭轉氣動力主要是由橫風向的旋渦脫落引起的;當厚寬比D/B＞1后，基底扭矩系數均方根值迅速增大，且遞增的趨勢逐漸加劇，這主要是由于當厚寬比D/B＞1后，扭轉氣動力主要是由尾流與再附著流引起的橫風向不對稱壓力而產生的，這一結論與Tamura(1996)的結論是一致的。

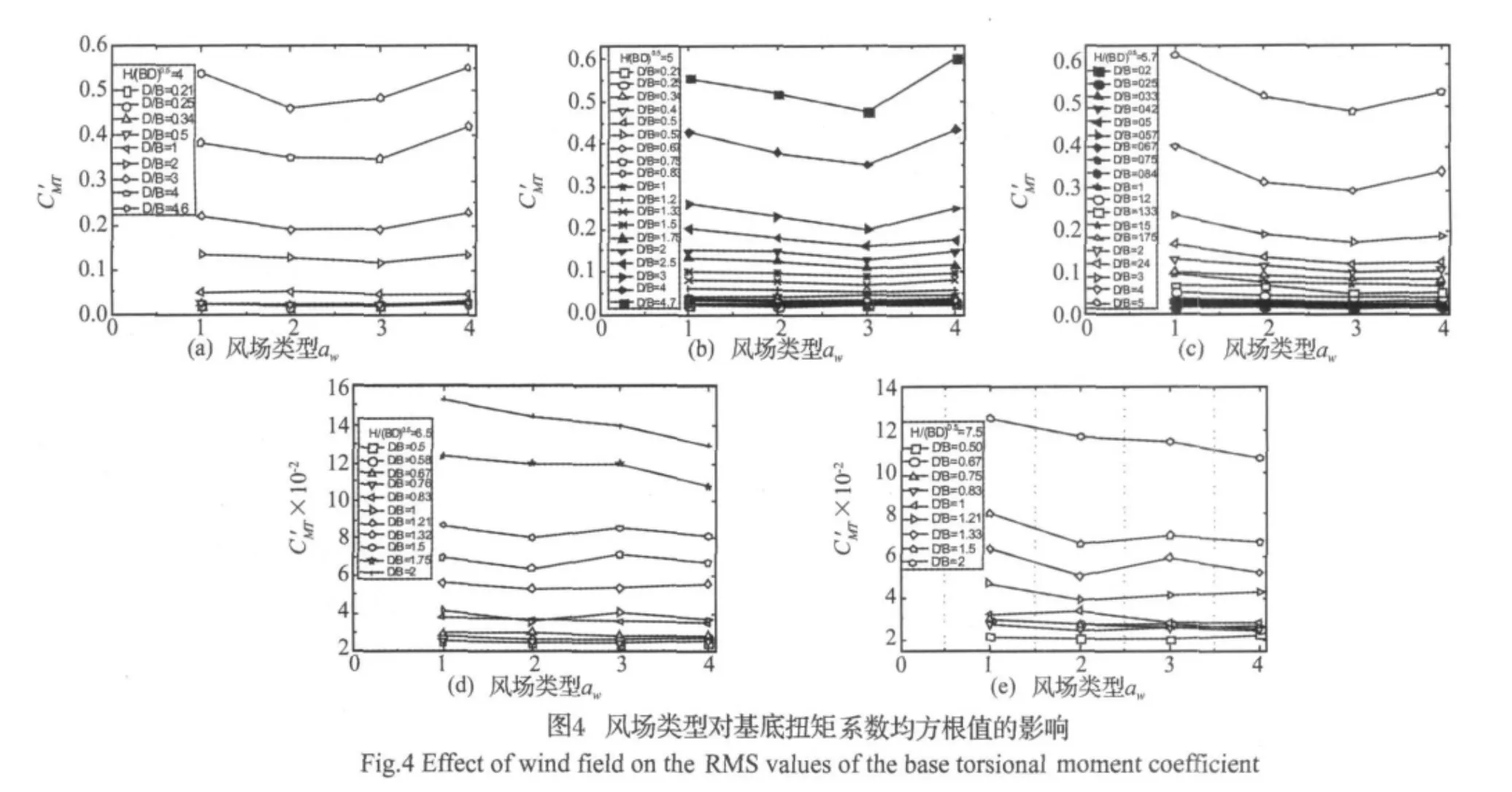
2.2 風場的影響

圖4給出了風場類型對基底扭矩系數均方根值的影響。從圖中可以看出，當厚寬比D/B≤2時，基底扭矩系數均方根值受厚寬比的影響較小，這主要是由于當厚寬比D/B≤2時，扭轉氣動力主要是由于橫風向的旋渦脫落引起的不對稱力而導致的，迎風面來流紊流的不對稱作用也對扭轉動荷載的貢獻較小;當厚寬比D/B＞2后，基底扭矩系數均方根值隨著湍流度的增大，先減小后增大，這主要是由于隨著厚寬比的增大，再附著流出現，湍流度的增大同時又加快了重附著流的出現，并且減小了旋渦脫落的強調，同時來流紊流的不對稱作用也對扭轉動荷載的貢獻也越來越大，這樣就導致了隨著湍流度的增大，基底扭矩系數均方根值先減小后增大。

2.3 長細比的影響

從圖4中可以看出，在一定的長細比下，風場類型對基底扭矩系數均方根值的影響隨著厚寬比D/B的不同而變化，不同長細比下風場類型對基底扭矩系數均方根值的影響在不同的厚寬比下基本一致，說明長細比對基底扭矩系數均方根值的影響不大。

2.4 擬合公式

根據上文的分析，基底扭矩系數均方根值的主要影響因素為厚寬比與風場類型(湍流強度)，長細比的影響比較小，可不予考慮。為了便于工程應用，基于上述試驗數據處理的結果，利用多參數的最小二乘法，擬合得到如下矩形截面基底扭矩系數均方根值的函數表達式:

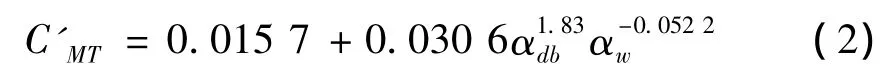
其中，αdb=D/B為建筑的厚寬比，B和D分別為建筑的迎風立面寬度和順風向厚度;αw為風場類型，1，2，3，4分別代表A，B，C，D四類風場。

為了能更好地量化分析擬合公式的誤差，定義誤差率如下:

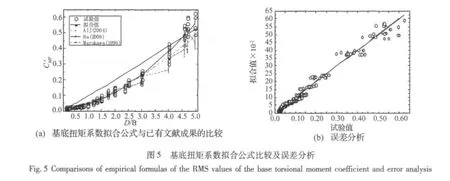
圖 5(a)中給出了本文擬合公式與 AIJ［7]、Ha［10]以及 Marukawa［5]的比較結果。Ha［10]公式計算結果比其他結果都要大，該擬合公式的計算結果較保守;當厚寬比小于3時，本文的擬合結果與試驗結果以及AIJ［7]和Marukawa［5]的計算結果都有很好的一致性;當厚寬比大于3 后，本文的計算結果比 AIJ［7]和 Marukawa［5]的計算結果稍有偏大，這主要是由于試驗風場條件不同而導致的微小差別。圖5(b)對擬合公式(2)的準確性進行了分析。可以看出試驗值比較均勻地分布于代表擬合值的直線的上下側，公式(2)的誤差率的平均值為0.38%，標準差為10.1%，擬合公式有很好的預測試驗結果。總之，式(2)計算結果不僅與原始數據相符，與其他文獻試驗結果比較也有較好的一致性，說明本文的擬合公式具有較高的準確性和可信度。

3 結論

本文利用高頻動態測力天平技術，在4種不同風場中對71種不同尺寸的矩形截面高層建筑剛性模型進行了測力試驗，對矩形截面高層建筑基底扭矩均方根系數進行了研究，得到了以下一些有意義的結論:

(1)在長細比與風場類型一定的情況下，基底扭矩系數隨D/B的增大而單調增加。當厚寬比D/B＜1時，扭轉氣動力主要是由橫風向的漩渦脫落引起的，基底扭矩系數增幅不大;當厚寬比D/B＞1后，扭轉氣動力主要是由尾流與重附著流引起的橫風向不對稱壓力而產生的，基底扭矩系數迅速增大，且增大的趨勢逐漸加劇;

(2)在一定的長細比下，風場類型對基底扭矩系數的影響隨著厚寬比D/B的不同而不同。當厚寬比D/B≤2時，基底扭矩系數受厚寬比的影響較小;當厚寬比D/B＞2后，基底扭矩系數隨著湍流度的增大，先減小后增大;

(3)長細比對基底扭矩系數的影響較小，在實際應用中可以不予考慮;

(4)本文給出的擬合公式考慮了厚寬比與風場類型對矩形截面高層建筑基底扭矩系數的影響，該經驗公式形式簡單，并且具有較高的準確性與可信度，可為實際應用及規范修訂提供參考。

［1] Simiu E，Scanlan R H.Wind effects on structures［M] .3rded.New York:John Wiley＆ Sons Ltd，1996.

［2] Marukawa H，Ohkuma T，Momomaura Y.Across-wind and torsional acceleration of prismatic high rise buildings［J] .Journal of Wind Engineering and Industrial Aerodynamic，1992，41 －44:1139 －1150.

［3] Choi H，Kanda J.Proposed formulae for the power spectral densities of fluctuating lift and torque on rectangular 3－D cylinders［J] .Journal of Wind Engineering and Industrial Aerodynamic，1993，46 －47:507 －516.

［4] Tamura Y，Kawai H，Uematsu Y，et al.Wind load and windinduced response estimations in the Recommendations for Loads on Buildings，AIJ 1993［J] .Engineering Structures，1996，18(6):399－411.

［5] Marukawa H，Ohkuma T.Formula of fluctuating wind forces for estimation of across-wind and torsional responses of prismatic high rise buildings［J] .Journal of Structural Construction Engineering of Japan，1996，482:33 －42.

［6] Yutaka A，Koji K，Kazuki H.Experimental research of aerodynamic force on rectangular prism［J] .Journal of Wind Engineering of Japan，2002，91:83－88.

［7] Architectural Institute of Japan.AIJ Recommendations for Loads on Buildings(English version)［M] .2004.

［8] Zhou Y，Kijewski H，Kareem A.Aerodynamic loads on tall building:Interactive database［J] .Journal of Structural Engineering，2003，129－394.

［9] Liang SG，Li Q S，Liu SC，et al.Torsional dynamic wind loads on rectangular tall buildings［J] . Engineering Structures，2004，26:129.

［10] Ha Y C，Kim Y S，Kim H R.Fluctuating torsional moment coefficient and power spectral density coefficient for estimating wind loadings on a tall building［C] .Proceedings of the 4th International Conference on Advances in Wind and Structures(AWAS'08)，Jeju，KOREA，May 29 －31，2008.

［11] 唐 意.彎扭耦合高層建筑風致振動及靜力等效風荷載［D] .上海:同濟大學土木工程學院，2006.