建筑材料特性對GPS監測信號影響規律的試驗研究

伊廷華， 張永恒， 李宏男， 顧 明

(1.大連理工大學 建設工程學部，遼寧 大連 116023;2.同濟大學 土木工程防災國家重點實驗室，上海 200092)

全球定位系統(Global Positioning System，簡稱GPS)因其具有高效、快速、全自動、全天候、高精度等優越性能而在大型工程結構健康監測中得到推廣應用，目前已從大壩監測、高邊坡監測和地面沉降監測逐步擴展到超高層建筑、大跨橋梁等結構系統的監測［1]。然而，GPS信號從20200 km的高空到達地面，受到多種誤差源的影響，在這些誤差源中，衛星和接收機鐘差、軌道誤差、大氣折射和延遲誤差等可通過雙差觀測或精確的數學模型予以消除，而多路徑誤差由于測站相關性很弱，即使很短的基線，兩站間多路徑影響差異也很大，站間求差方法對多路徑誤差的消除作用不大，且沒有較好的模型來改正，多路徑效應已成為影響高精度定位的主要制約因素之一［2]。

研究多路徑信號的規律并尋求合適的消噪方法已成為國內外學者研究的熱點。過靜珺等［3]通過在GPS接收機天線1 m處放置不同反射板進行了短時間的靜態觀測，得到了多路徑效應與反射材料有關的初步結論。楊天石等［4]將一臺GPS接收機安置在距離墻面0.9 m處進行了2 h的數據采集，研究了利用信噪比消除多路徑誤差的方法。車偉等［5]提出了一種削弱GPS多路徑誤差影響的附加參數法，并在GPS天線旁放置一塊傾斜的反射板來驗證該方法的有效性。伊廷華等［6]利用瓷磚墻面的反射，進行了連續3 d的GPS多路徑信號的采集，提出了一種基于自適應噪聲抵消與小波濾波相結合的GPS噪聲抑制方法。Bétaille等［7]提出了一種多路徑自適應法則，并將一鋼板置于距GPS接收機天線不同的位置分別進行靜態和動態觀測來驗證該方法的有效性。Tambuwala等［8]將不同的材料放在距接收機天線約15m處進行數據采集來得到不同材料對 locata信號傳播的影響。Kijewski-Correa等［9]在通過一塊的薄鋁板，得到了接收機的系統噪聲以及多路徑效應引起的誤差。Lau等［10]引入一種射線跟蹤方法對GPS載波相位多路徑進行模型化來消除其影響，試驗表明，該方法在鋼板和磚墻的反射環境下比較有效，而在水面反射時并不理想。Lee等［11]以空間統計理論為基礎建立了一套模擬系統來削減多路徑誤差和提高GPS定位的精度，并以典型的建筑材料作為反射物實驗得到了反射信號的衰減值。

從上面的分析可以看到，目前研究者主要從信號的內部結構出發，試圖建立一種通用的多路徑誤差修正模型，效果并不理想，這是由于每個GPS天線的安裝位置是不同的，它們所處的周邊環境也就不同，不同環境的反射介質將會引起不同的多路徑誤差。因此，系統地研究并歸納出不同建筑材料對GPS信號的影響規律，對修正GPS定位結果，尋找合理的濾波方法，進而提高GPS的監測精度，具有重要的意義。

1 載波相位測量中GPS多路徑信號特征分析

GPS衛星信號從高空向地面發射，若接收機天線周圍有高大建筑物或水面時，會對電磁波產生很強的反射作用，天線接收的信號不但有直接從衛星發射的信號，還有經過反射的電磁波信號，這兩種信號會產生干涉，從而使觀測值偏離真實值，這種由多路徑的信號傳播所引起的干涉時延效應稱為多路徑效應(Multipath Effect)［12]。影響多路徑誤差的因素主要有:① 反射點衛星信號的入射角;② 衛星信號的載波波長;③ 反射物的反射系數;④ 接收機天線到反射面的水平距離。

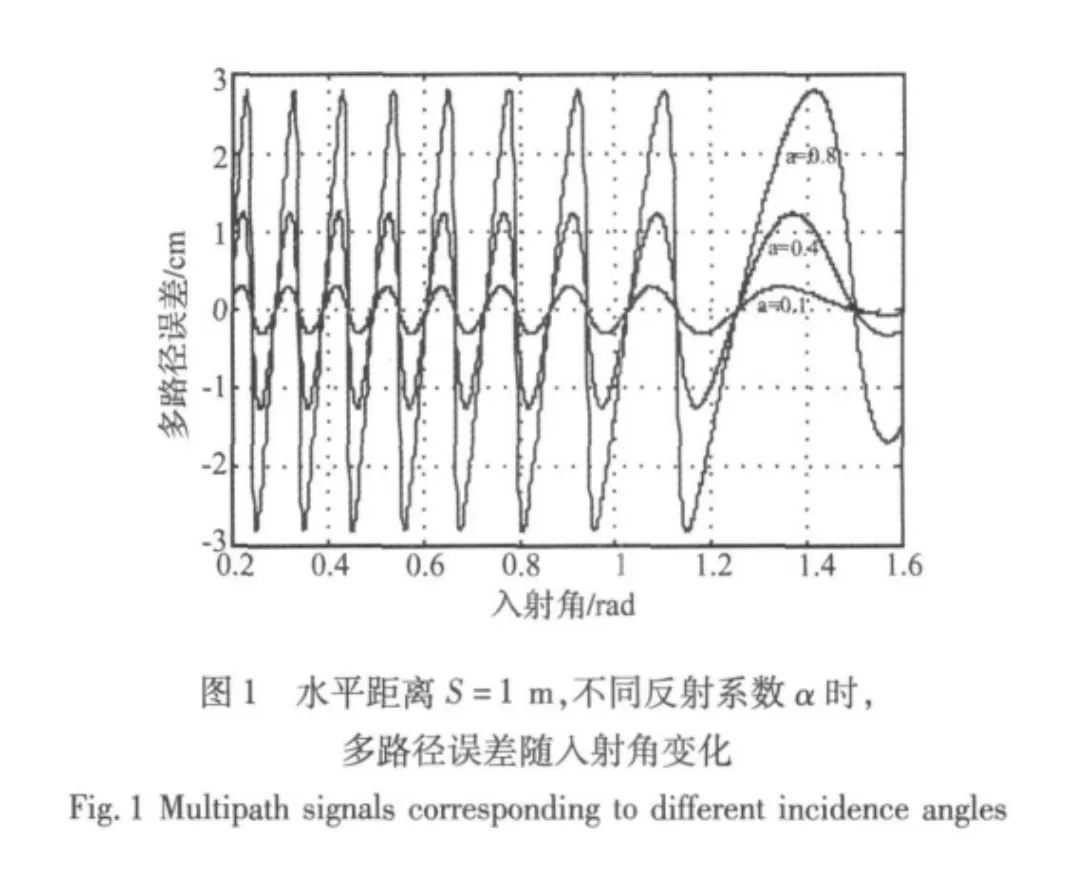
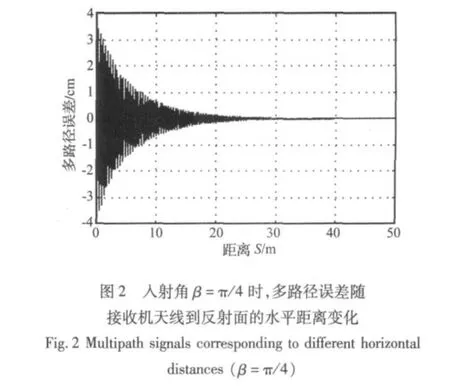
目前，利用GPS進行結構監測時，最常用的是雙頻載波相位測量。即有兩個頻率，一個為L1=1 575.42 MHz，另一個為 L2=1 227.60 MHz。這里以 L1載波(λ=0.19 m)為例，取水平距離為1 m時，入射角 β=［10，90] ≈［0.2，1.6] ，對不同反射系數 α =0.1，0.4 和0.8三種情況下多路徑誤差隨反射面的入射角β變化進行仿真，如圖1所示。從圖中可以看到，隨著反射系數的增加，多路徑誤差的幅值逐步增大。眾所周知，反射系數與反射介質的材料有關，對于非金屬材料，其產生的多路徑效應與介電常數有關，介電常數越大反射越大，反之愈小。多路徑效應除了與介電常數有關外，還與反射物與天線距離有關，當反射物距離天線為10 m時，衛星信號功率衰減1/10;距離20 m時衰減40 dB;距離為50 m時信號衰減100 dB［13]。電磁波在大氣中傳播呈指數衰減，考慮到信號入射角為π/4時，距離由0變化到50 m的過程中，對多路徑誤差隨接收機天線到反射面的水平距離的變化進行仿真，如圖2所示。可以看到，當反射物距天線距離超過50 m時，就無需考慮其對直接波產生的影響了。

2 試驗研究與數據分析

2.1 GPS監測系統的設計與建立

為了研究不同建筑材料引起多路徑誤差的規律，設計了一套GPS多路徑信號模擬與監測系統。試驗選在凈空較好的大連理工大學綜合試驗1號樓樓頂，設計的GPS監測系統如圖3所示。基準站采用瑞士Leica公司生產的GR×1200 Pro GPS信號接收機，流動接收機為GM×902型GPS信號接收機;基準站和流動站接收機均采用A×1202 GG天線，其內置的抑徑板可有效地抑制多路徑，為單站和參考站發送高質量的GPS觀測信號。基準站接收機天線設在樓頂電梯房的頂部，附近沒有遮擋物;流動站接收機天線設在樓頂上，周圍50 m內沒有遮擋物，可基本認為不受多路徑效應的影響。

圖3 GPS監測系統組成示意圖Fig.3 Compositions of GPSmonitoring system

本系統采用的是網絡傳輸的數據傳輸方式，相比較無線傳輸，這種方式更加穩定、準確。基準站、流動站和控制中心(數據處理與管理部分)通過網絡交換機組成了一個局域網，如圖4和圖5所示。基準站接收機接收的信號可以直接通過網絡傳輸，流動站接收機接收的信號要通過RS232協議傳輸，這里通過一個串口服務器將RS232協議的信號轉換成IP協議的信號再通過網絡傳輸。

數據處理及管理部分(控制中心)設在樓頂的電梯房內，由一臺計算機安裝相應的總控軟件、數據處理和分析軟件等組成。總控軟件采用Leica GNSS Spider軟件，可控制接收機并對它們進行設置，用于數據記錄和RTK/DGPS數據播發，同時可管理數據的下載、壓縮、存檔和分發，并對整個網絡進行監測。Leica GNSS QC軟件能夠對觀測到的數據進行質量評價、信噪比分析、坐標分析等。

圖4 系統實際布設圖Fig.4 Set-up of GPSmonitoring system

2.2 主要試驗過程

圖5 系統連接圖Fig.5 Configuration of GPSmonitoring system

試驗主要包括三個階段:① 在接收機天線旁不放置任何反射物，進行連續一天的靜態觀測，獲取流動站的測站坐標;② 為了檢驗接收機的系統噪聲，在接收機天線周圍50 m內不放置反射物，進行連續三天的實時動態數據采集;③ 為了研究反射物的材料以及反射物到接收機的距離產生的多路徑誤差的變化規律，試驗過程中選用三種常見的建筑材料壓制木板、PVC板和瓷磚作為反射物，三種材料的介電常數見表1所示。首先選用壓制木板作為反射物進行試驗，試驗中木板被固定在鋼支架上，并且木板與地面垂直，然后將反射板分別放置在距離流動站接收機天線1 m、4 m和7 m處(不同距離時反射板的高度根據接收機的截止衛星高度角計算得到)，如圖6和圖7所示，每個距離進行連續兩天的實時動態觀測，共計6天。以壓制木板作為反射物完成試驗后，再分別以PVC板和瓷磚為反射物進行試驗。試驗過程中實時動態數據采集均設置截止衛星高度角為10°，采樣頻率為10 Hz。

表1 三種反射材料的介電常數Tab.1 Dielectric constant of three different materials

2.3 多路徑誤差的變化規律研究

由于Leica GNSSSpider軟件直接輸出的是WGS－84坐標，首先通過三參數方法將其轉換為北京54平面直角坐標，然后將試驗過程②的結果減去試驗過程①靜態條件下測得的流動站坐標，即可就得到連續三天東西、南北及高程方向上接收機的系統噪聲。由于采用的是差分GPS定位，可消除基準站和流動站的公共誤差;試驗過程③測得的結果僅受多路徑誤差和接收機系統噪聲的影響。因此，試驗過程③測得的結果與流動站坐標求差后得到的為多路徑誤差和接收機噪聲的疊加序列。為了研究反射物的材料以及反射物到接收機天線的距離對GPS信號的影響規律，試驗③的過程中每種材料在每個距離進行連續兩天的數據采集，從天氣狀況較好的一天中各取1h的數據進行比較，第二天比第一天提前3 min 56 s，依次類推，共9組數據。

研究多路徑信號的變化規律，可利用改進的粒子濾波算法對試驗數據進行處理［14]。粒子濾波算法早期的形式是序貫重要性采樣算法，但是該算法存在嚴重的退化問題，為了解決該問題，出現了一些改進算法，如多項式重采樣算法，殘差重采樣算法，分層重采樣算法和系統重采樣算法。由于系統重采樣算法在運算時間、估計精度和計算復雜程度方面要優于其它幾種算法［15]，因此，這里采用系統重采樣算法的粒子濾波來對數據進行處理。

(1)同種材料在不同距離時對GPS信號的影響規律

由于同種材料在不同的距離引起的多路徑誤差變化規律具有相似性，又為了節省篇幅，下面以木板為例來研究多路徑誤差的變化規律。試驗時，木板沿高度角分別置于1 m、4 m和7 m處，如圖8所示。基于試驗過程(2)測得的接收機噪聲的特性，利用改進的粒子濾波處理后的數據如圖9所示。

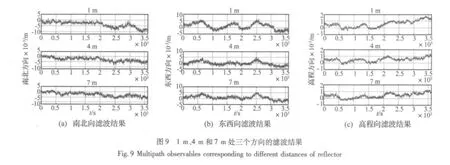
由濾波后1 m、4 m和7 m的結果可以得到多路徑序列的幅值和標準差變化如表2，相關性變化如表3。從表2中可以看出，除東西方向最小值變化不明顯以外，其他的多路徑誤差幅值在三個方向上都隨著距離的增加而減小，而且減小的幅度也在變小;高程方向的多路徑誤差變化范圍比平面內的要大，大約是2倍的關系;多路徑誤差的標準差在三個方向上隨著距離的增加也都減小，這說明多路徑誤差序列變得越來越平緩;從表3中可以看出，隨著距離的增加，多路徑誤差雖然有一定的相關性，但相關性變得越來越小。

(2)不同材料在在相同距離時對GPS信號的影響規律

經過濾波后，三種不同的反射材料在1m、4m和7m處在南北、東西和高程方向上引起的多路徑誤差序列如圖10～圖12所示。

表2 濾波后多路徑誤差序列的幅值和標準差(單位:cm)Tab.2 Amplitude and standard deviation of multipath signals after filtering(Unit:cm)

表3 濾波后多路徑誤差序列相關性變化Tab.3 Correlation coefficients of multipath signals after filtering

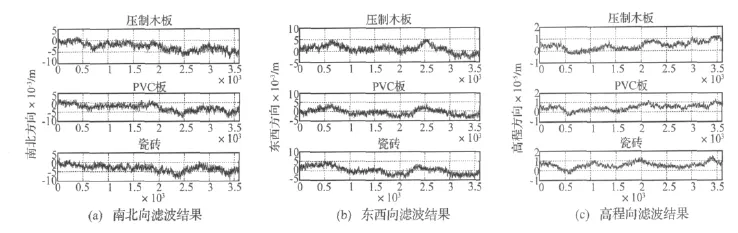
圖12 7 m處三種材料在三個方向上的濾波結果Fig.12 Monitoring signals when the reflector is at 7 m after filtering

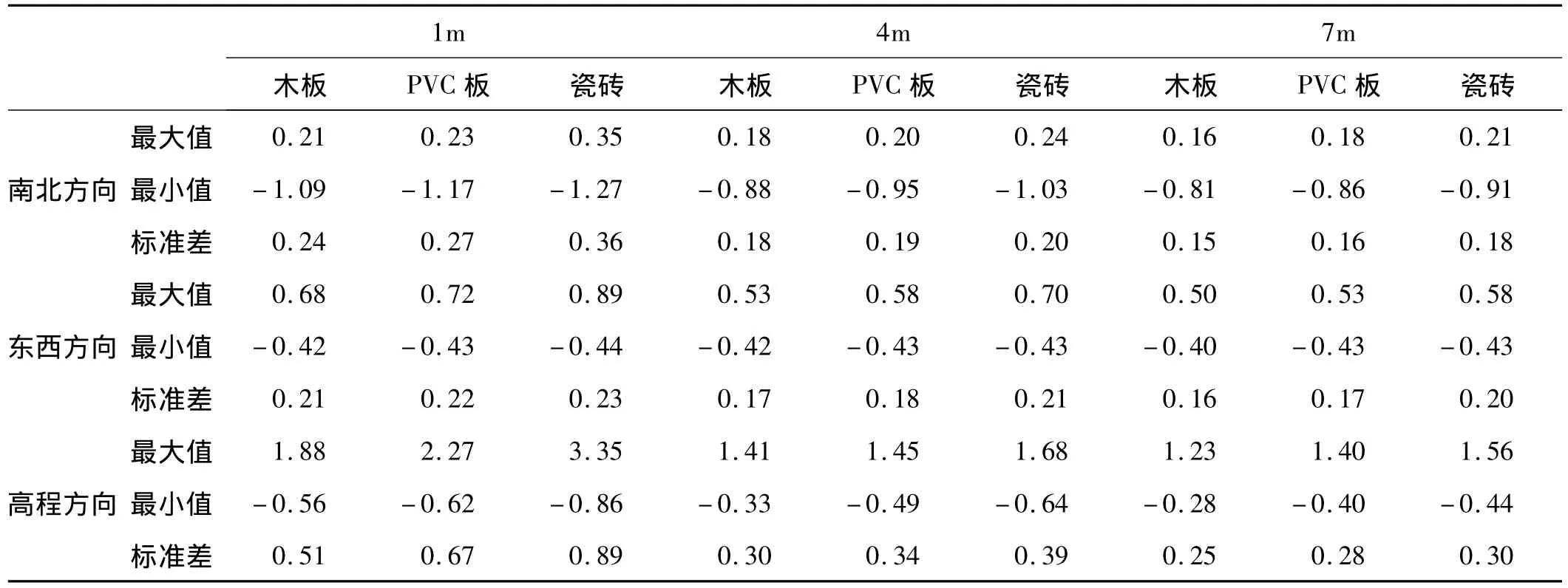
表4 1 m、4 m和7 m處三種材料引起的多路徑誤差序列的幅值和標準差變化(單位:cm)Tab.4 Amplitude and standard deviation of multipath signals after filtering(Unit:cm)

表5 1 m、4 m和7 m處濾波后多路徑誤差序列相關性變化Tab.5 Correlation coefficients of multipath signals after filtering

由濾波后三種材料在1 m、4 m和7 m的結果可以得到多路徑誤差序列的幅值和標準差變化分別如表4所示，相關性變化如表5。由表4可以看出，除東西方向最小值變化不明顯以外，其它的多路徑誤差幅值在三個方向上都隨著材料介電常數的增加而增加，而且增加的幅度與材料的介電常數有關;多路徑誤差的標準差在三個方向上也隨著材料介電常數的增加而增加;從表5中可以看出，在同一距離時，三個方向上壓制木板與PVC板相關性比PVC板和瓷磚的相關性要大;隨著距離的增加，兩種材料產生的多路徑誤差雖然有一定的相關性，但相關性變得越來越小。

3 結論

本文對GPS多路徑信號的規律性進行了仿真分析，設計了一套完整的GPS多路徑信號模擬與監測系統，在此基礎上選擇三種不同介電常數的木板、PVC板和瓷磚進行了GPS多路徑試驗，利用改進的粒子濾波算法對試驗測得的數據進行了處理。結果表明:同種材料在不同距離引起的多路徑誤差和不同材料在同一距離引起的多路徑誤差都具有一定的規律性。

對同種反射物在不同的距離時引起的多路徑誤差的規律進行研究，得到了以下結論:

(1)隨著距離的增加，多路徑誤差其相關性變得越來越小，且多路徑誤差的變化趨勢趨于平緩;

(2)在增加相同距離的情況下，多路徑誤差減小的幅度也在變小;

(3)高程方向的多路徑誤差比南北和東西方向的多路徑誤差大;

對不同的反射物在相同的距離時引起的多路徑誤差規律的研究，得到了以下結論:

(1)隨著材料介電常數的增加，多路徑誤差越來越大，而且增加的幅度與材料的介電常數有關;

(2)隨著距離的增加，兩種材料產生的多路徑誤差雖然有一定的相關性，但相關性越來越弱。

［1] 伊廷華，李宏男.結構健康監測—GPS監測技術［M] .北京:中國建筑工業出版社，2009.

［2] 李宏男，伊廷華，王國新.GPS在結構健康監測中的研究與應用進展［J] .自然災害學報，2004，13(6):122－130.

［3] 過靜珺，商瑞斌，李毓麟.多路徑效應對GPS定位影響的研究［J] .工程勘察，1995，2:46－49.

［4] 楊天石.多路徑效應對GPS精密定位的影響及消除方法分析［J] .勘查科學技術，2006，(3):53－56.

［5] 車 偉，熊永良.變形監測中基于信號反射預計的GPS多路徑誤差減弱方法［J] .四川測繪，2007，30(1):7 －10.

［6] 伊廷華，李宏男，伊曉東，等.基于自適應噪聲抵消與小波濾波的GPS監測誤差分析［J] .武漢大學學報(信息科學版)，2006，31(11):995－998.

［7] Bétaille D F，Cross P A.Euler H J.Assessment and Improvement of the capabilities of a window correlator to model GPSmultipath phase errors［J] .IEEE Transactions on Aerospace and Electronic Systems， 2006，42(.2):705－717.

［8] Tambuwala N，Jamaluddin M.Effect of different construction materials on the propagation of Locata's 2.4GHz signal［C] .International Global Navigation Satellite Systems Society IGNSSSymposium，2007.

［9] Kijewski-Correa T，Kochly M.Monitoring the wind-induced response of tall buildings:GPSperformance and the issue of multipath effects［J] .Journal of Wind Engineering and Industrial Aerodynamics，2007，95(9 －11):1176 －1198.

［10] Lau L，Cross P.Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling［J] .Journal of Geodesy，2007，81(11):713 －732.

［11] Lee Y W，Suh Y C，Shibasaki R.A simulation system for GNSS multipath mitigation using spatial statistical methods［J] .Computers＆Geosciences，2008，34:1597 1609.

［12] 伊廷華，張永恒，李宏男，等.多路徑效應在GPS結構健康監測中的研究進展［J] .振動與沖擊，2009，28(9):102－108.

［13] 袁林果，黃丁發，丁曉利，等.GPS載波相位測量中的信號多路徑效應影響研究［J] .測繪學報，2004，33(3):210－215.

［14] Yi T H，Zhang Y H，Li H N，et al.Research on GPS multipath effect based on improved particle filtering algorithm［C] . The 8th International Conference on Civil and Environmental Engineering(ICCEE 2009).Oct.，28 －30，2009，Busan，Korea.

［15] 馮 馳，王 萌，汲清波.粒子濾波器重采樣算法的分析與比較［J] .系統仿真學報，2009，21(4):1101 －1105.