神舟飛船平移發動機對太陽能帆板羽流效應數值模擬研究

蔡國飆 賀碧蛟

（北京航空航天大學宇航學院）

1 引言

飛船、空間站等大型航天器具有質量大、艙段多的特點，其上需要布置多塊太陽能帆板才能滿足航天器對電力的需求。由于帆板數量較多，對與部分發動機距離較近的帆板，發動機真空羽流會對其產生較大的氣動力和力矩作用。為了對發動機真空羽流效應進行數值模擬，必須針對不同的流動狀態建立相應的數學物理模型，并采用與之相應的數值模擬方法。目前能夠比較成功地模擬真空羽流效應的研究方法是直接模擬蒙特卡羅方法[1]（DSMC）。

國外針對發動機羽流問題的研究開展得比較早，開發了一系列基于DSMC的模擬計算軟件，其中比較典型的通用計算軟件有：由美國約翰遜航天中心（Johnson Space Center）的 LeBeau[2-4]等人開發的DAC（DSMC Analysis Code）軟件，由俄羅斯理論與應用機械研究所（the Institute of Theoretical and Applied Mechanics）的 Ivanov[5]等人開發的 SMILE（Statistical Modeling In Low-density Environment）軟件，由美國Cornell大學的Dietrich和Boyd等人開發的MONACO 計算軟件[6，7]等。

文章所介紹的基于 DSMC的 PWS（Plume WorkStation）羽流計算軟件是依據模塊化的原則，適當引入面向對象的編程思想，特別設計具有較強通用性的粒子邊界處理模塊，實現PWS軟件在羽流模擬計算的通用化，并在國外“CUBRC”試驗研究的基礎上開展試驗驗證工作。使用PWS軟件就神舟飛船120N平移發動機羽流對太陽能帆板氣動力效應進行了數值模擬研究，并且對比了由不同帆板角度對作用在帆板中心點的力和力矩影響。

2 羽流數值模擬模型和方法

流場依據Knudsen（Kn）數劃分為三大領域，即連續流區領域（Kn＜0.1）、過渡領域（0.1＜Kn＜10）和自由分子流領域（Kn＞10）[8]，Kn= λ/L，其中 λ 是平均分子自由程，L為流動特征長度。在Kn數較大，即氣體變稀薄時，基于連續流介質的N-S方程失效。

真空羽流流場包括了全部流態，即連續介質流、過渡領域流和自由分子流等[1]。羽流核心區為連續流，外圍為過渡領域流和自由分子流，羽流流動極為復雜，很難用一種方法來描述。對于連續流動，對應的數學方程是N-S方程；對于自由分子流，對應的數學方程是無碰撞項的Boltzmann方程；而對于過渡領域流的研究，目前尚無完善的理論，與之相對應的數學方程是完全的Boltzmann方程，它是一個非常復雜的非線性積分-微分方程，除了極其簡單的情形，它的理論求解極為困難。

為了對羽流流場進行數值模擬，必須針對不同的流動狀態建立相應的數學物理模型，并采用與之相應的數值模擬方法。目前能夠比較成功地模擬自由分子流和過渡領域流的數值方法是DSMC。DSMC方法是20世紀60年代初由G.A.Bird提出并發展的直接模擬方法，在數學上已被證明與Boltzmann方程的相容。

G.A.Bird[1]提出的DSMC直接從物理實際出發，利用少量的模擬分子代替真實流場內數目眾多的氣體分子，用計算模擬代替物理過程，經統計平均獲得宏觀流動參數，達到求解稀薄氣體問題的目的。典型的DSMC計算流程圖如圖1所示。

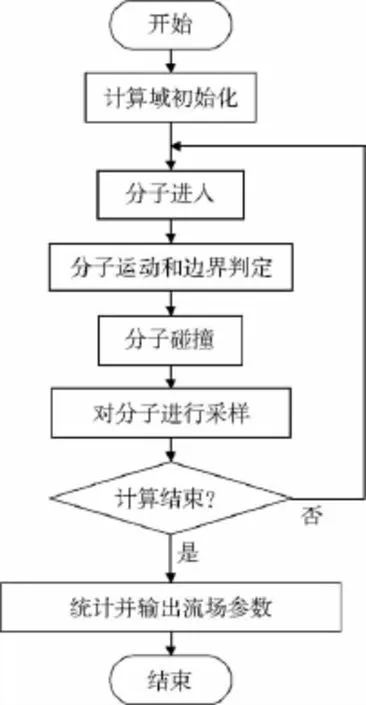
圖1 DSMC計算流程圖

由于羽流場DSMC計算域的密度值較低，分析時常作如下假設：（1）流場中分子的碰撞為二體碰撞；（2）由于氣體溫度不高，僅考慮分子的轉動內能，忽略分子的振動內能和分子化學非平衡效應；（3）氣體流動為定常流動；（4）將分子視為變徑硬球分子（VHS）。

3 PWS軟件及驗證

DSMC使用大量的“模擬分子”以模擬真實的氣體，為此需要較大的存儲空間和較高計算速度，這極大地限制了DSMC的應用。DSMC的計算主程序主要有6個主模塊：粒子模塊（粒子參數存儲）、網格模塊、粒子進入模塊、粒子運動模塊、邊界模塊（主要指固體邊界）和粒子碰撞模塊。考慮到計算速度的需要，在6個主模塊的基礎上再增加一個并行模塊。在羽流效應計算時，DSMC的各模塊信息交換如圖2所示。

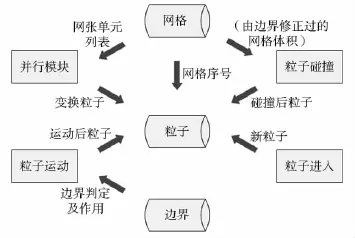
圖2 DSMC計算模塊信息交換關系圖

根據模塊化和面向對象的軟件設計方法，PWS軟件對DSMC計算程序進行如下改進：

（1）使用松散的軟件架構保證各個計算模塊的相對獨立性，即改進其中一個模塊時，基本上不需要改動其他模塊；

（2）對各個模塊的功能實現采用通用性設計，即在使用單/多組分分子、不同分子模型（碰撞模型和內能模型）、不同固體邊界條件時不需要改動源代碼。

如圖2所示，基于DSMC的PWS羽流計算通用軟件主要包括網格模塊、粒子參數模塊、粒子進入模塊、粒子運動及邊界模塊、粒子碰撞模塊、并行模塊模塊6大模塊。在這6大基本模塊的基礎上，針對各種實際問題（單組分、多組分、多種碰撞模型、多種邊界條件），PWS羽流計算軟件可以方便地搭建數值模擬應用平臺。

軟件計算結果的驗證是軟件編制不可缺少的一環。本文使用了美國Holden[9]等人做的“CUBRC”第7次試車數據作為軟件計算驗證的對比數據。“CUBRC”實驗是一個超音速稀薄氣流對雙圓錐體的氣動力和氣動加熱效應的測量試驗，試驗用的雙圓錐體構型如圖3所示。圖4為利用PWS軟件對雙圓錐體表面壓強分布的計算結果與試驗測量數據對比圖，圖5為利用PWS軟件對雙圓錐體表面熱流密度分布的計算結果與試驗測量數據對比圖，軸向距離X指從雙圓錐體的頂點為原點，計算點在雙圓錐體的中心線上投影的坐標值（m）。

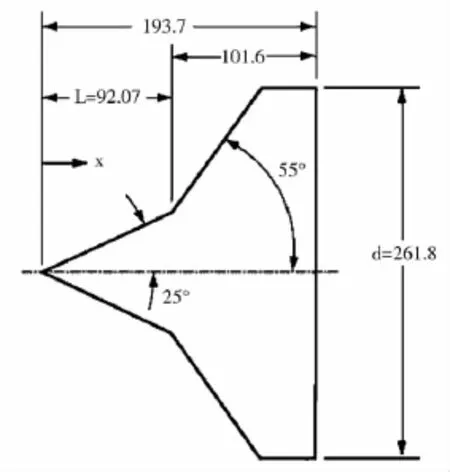
圖3 “CUBRC”試驗雙圓錐體結構圖（單位：mm）

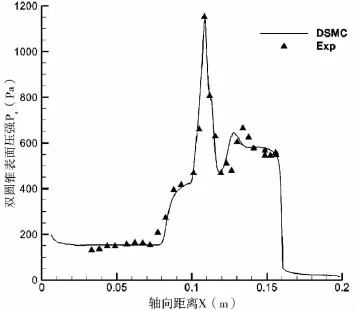
圖4 雙圓錐體表面壓強分布計算值與試驗值對比

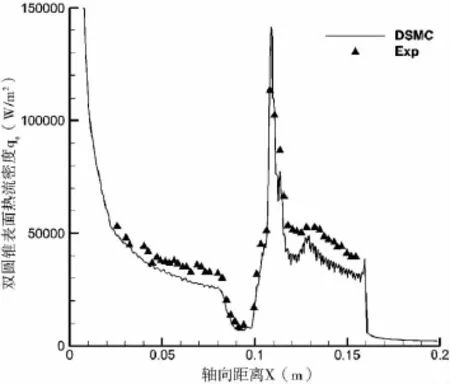
圖5 雙圓錐體熱流密度分布計算值與試驗值對比

從圖4、圖5可以看出雙圓錐體表面壓強和熱流密度計算值與試驗值相符，最大值和最小值的位置一致；除了2個點之外，其他各點的壓強計算值相對試驗值的偏差都在±20%以內；熱流密度計算值相對試驗值的偏差都在-30%～+10%范圍以內，特別是在雙圓錐連接處附近符合得相當好。經過與實驗值比對，可以認為PWS計算軟件具有較高的置信度。

4 太陽能帆板羽流效應計算

神舟飛船平移發動機推力相對較小，故可直接將發動機出口截面作為DSMC計算的模擬分子入口條件，使用PWS軟件直接對發動機三維羽流場進行數值模擬，得到發動機單機/雙機工作時羽流對太陽能帆板在0°、45°和90°三種狀態下產生的氣動力效應值，具體計算算例如表1所示。發動機與太陽能帆板的相對位置如圖6所示。

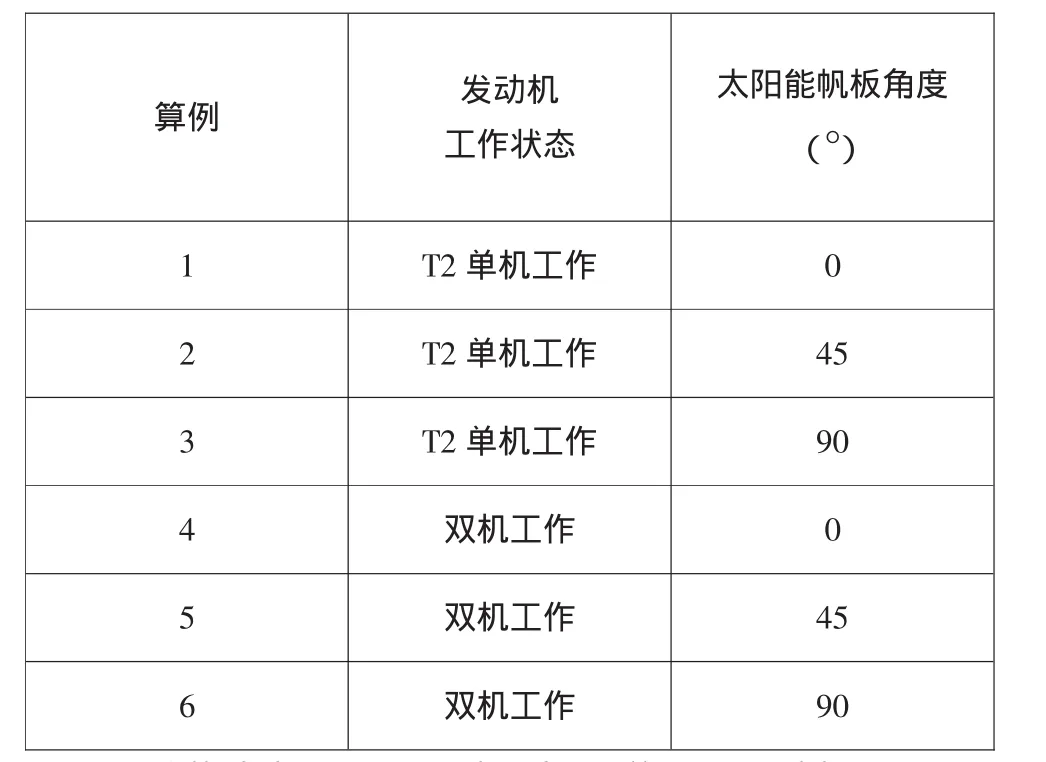
表1 對比算例

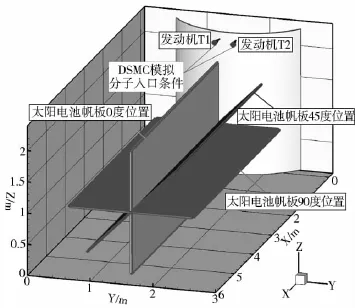
圖6 發動機與太陽能帆板相對位置

4.1 計算條件

（1）粒子入口條件

粒子入口條件為：以發動機出口截面作為PWS軟件計算外噴流和后流區的粒子入口截面條件；“模擬粒子”選取燃燒產物主要組分 N2、H2O、CO、CO2和H2等5種氣體分子，質量分數如表2所示。

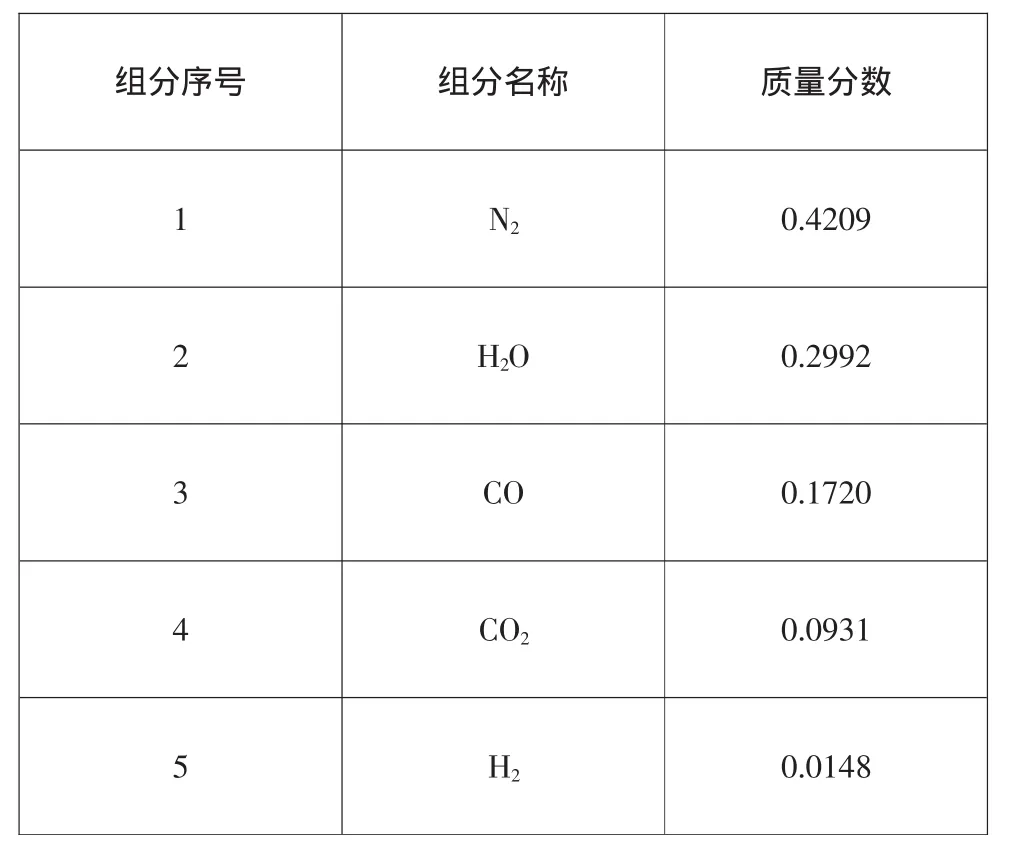
表2 發動機燃燒產物主要組分質量分數

粒子入口截面物理相對值分布如圖7所示，圖中各參考量的的定義為：參考密度ρ0=0.005kg/m3，參考壓強P0=2000Pa參考溫度T0=3000K，參考軸向速度u0=3500m/s，參考徑向速度v0=500m/s，發動機出口半徑R0=0.039m。

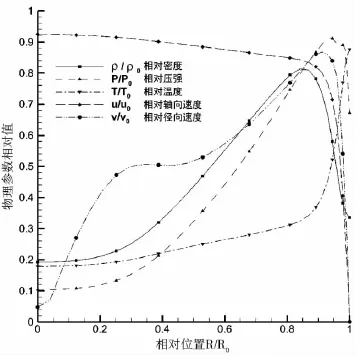
圖7 粒子入口物理參數分布圖

（2）邊界條件

真空邊界：粒子經過真空邊界后逃逸（即刪除）；

固體邊界：粒子撞擊到固體邊界按照Maxwell反射[1]處理，Maxwell反射需確定固體邊界壁面溫度和熱適應系數，發動機壁面溫度設定為800 K，飛船和太陽能帆板表面溫度設定為300 K，熱適應系數統一設定為1。

4.2 計算結果與分析

圖8至圖 13為算例1至算例6太陽能帆板所受的發動機羽流氣動壓強分布圖，圖中P指的是太陽能帆板表面正壓強（Pa）。

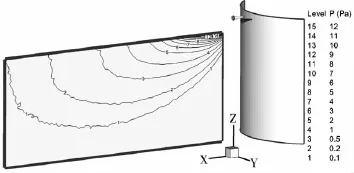
圖8 算例1太陽能帆板受到的羽流氣動壓強分布圖

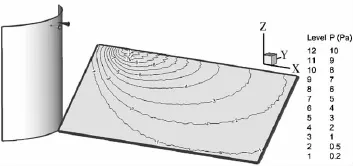
圖9 算例2太陽能帆板受到的羽流氣動壓強分布圖

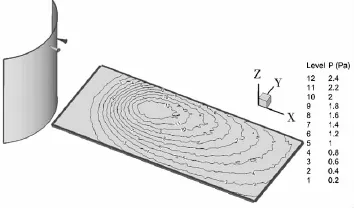
圖10 算例3太陽能帆板受到的羽流氣動壓強分布圖

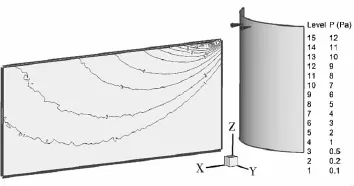
圖11 算例4太陽能帆板受到的羽流氣動壓強分布圖

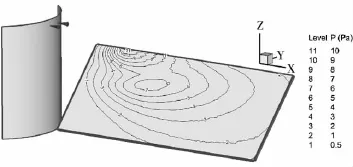
圖12 算例5太陽能帆板受到的羽流氣動壓強分布圖

從圖8至圖 13可以看出T1和T2平移發動機羽流對太陽能帆板的氣動壓強分布：T2發動機單機工作時羽流對0°狀態太陽能帆板氣動壓強最大值達到12Pa，且壓強值在1Pa以上的作用面積較小；T2發動機單機工作時羽流對45°狀態太陽能帆板氣動壓強最大值達到10Pa，且壓強值在1Pa以上的作用面積較大；T2發動機單機工作時羽流對90°狀態太陽能帆板氣動壓強最大值僅達到2.4Pa，但壓強值在1Pa以上的作用面積較大；T1和T2發動機雙機工作時羽流對0°狀態太陽能帆板氣動壓強最大值依然為12Pa，且壓強值在1Pa以上的作用面積與單機工作相比有所增加，但還是較小；T1和T2發動機雙機工作時羽流對45°狀態太陽能帆板氣動壓強最大值達到10Pa，且壓強值在1Pa以上的作用面積很大；T1和T2發動機雙機工作時羽流對90°狀態太陽能帆板氣動壓強最大值達到7.5Pa，且壓強值在1Pa以上的作用面積很大。這些說明，最大氣動力效應工況應該出現在雙機工作的45°或90°位置。表 3為六種工況下作用點為太陽能帆板的中心點的力和力矩的值。

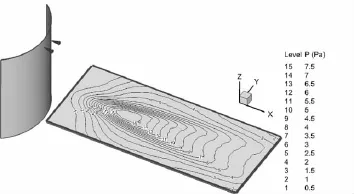
圖13 算例6太陽能帆板受到的羽流氣動壓強分布圖

從表3可以看出，發動機羽流對太陽能帆板影響最大的工況出現在算例5，即雙機工作時帆板處于45°角位置時，其作用在帆板中心點上的合力為約為24N，合力矩約為7.7Nm。

5 結束語

PWS軟件是一款基于DSMC的羽流計算通用軟件，并且具備了可擴展特性，松散的架構為軟件的進一步完善提供了方便的接口，軟件的計算值與國外“CUBRC”試驗測量值符合得很好，認為PWS軟件具有較高的置信度。

使用PWS軟件對神舟飛船平移發動機羽流效應進行計算表明：發動機羽流對著太陽能帆板羽流氣動壓強最大值出現在的算例1和算例4，即單機和雙機工作時帆板處于0°角位置時，但作用力不大；發動機羽流對太陽能帆板影響最大的工況出現在算例5，即雙機工作時帆板處于45°角位置時，其作用在帆板中心點上的合力約為24N，合力矩約為7.7Nm。

平移發動機對處于羽流直接撞擊區的太陽能帆板有較大的力效應作用，需要結合飛船質心進行進一步分析，數值模擬結果可以為神舟飛船平移發動機使用模式提供一定參考作用。 ◇

［1］Bird G A.Molecular gas dynamics［M］.Oxford:Clarendon Press，1976

［2］Wilmoth R G，Carlson A B，LeBeau G J.DSMC grid methodologies for computing low-density.hypersonic flows about reusable launch vehicles，AIAA 1996-1812［R］

［3］Boyles K A，LeBeau G J，Lumpkin III F E.The use of virtual subcells in DSMC analysis of orbiter aerodynamics at high altitudes upon reentry.AIAA 2003-1030［R］

［4］LeBeau G J，Boyles K A，Lumpkin III F E.Virtual sub-cells for the direct simulation Monte Carlo method.AIAA 2003-1031［R］

［5］Ivanov M S，Markelovf G N，Gimelshein S F.Statistical simulation of reactive rarefied flows:numerical approach and applications.AIAA 1998-2669［R］

［6］Dietrich S，Boyd I D.A scalar optimized parallel implementation of the DSMC method.AIAA 1994-355［R］

［7］Dietrich S，Boyd I D.Parallel implement at ion on the IBM SP-2 of the Direct Simulation Monte Carlo method.AIAA 1995-2029[R]

［8］沈青.稀薄氣體動力學［M］.北京：國防工業出版社，2003

［9］Holden M，Wadhams T.Code validation study of laminar shock/boundary layer and shock/shock interactions in hypersonic flow.Part A:experimental measurements，AIAA 2001-1031［R］