采用統一強度理論的錨噴支護圍巖彈塑性統一解
鄭強,林從謀,孟凡兵
(華僑大學巖土工程研究所,福建泉州 362021)
采用統一強度理論的錨噴支護圍巖彈塑性統一解
鄭強,林從謀,孟凡兵
(華僑大學巖土工程研究所,福建泉州 362021)
基于雙剪統一強度理論,結合點錨式錨桿錨噴支護的力學機理,導出雙向等地應力情況下無限均勻介質中錨噴支護圓形洞室圍巖應力場、位移場及塑性區半徑解析解.分析強度理論參數b值對彈性區和塑性區應力、位移的分布特點的影響,以及錨噴支護對塑性區半徑影響的變化趨勢.結果表明:與Morhr-Coulomb強度理論結果相比,隧道軸向應力和強度理論中的參數b對隧道圍巖應力場、位移場、塑性區半徑及支護反力等均有影響;圍巖應力值在錨固區外端位置有一個跌落;錨固區外端在塑性區的圍巖應力跌落比在彈性區時大,隧道圍巖塑性區半徑隨著錨固區半徑先增大而減小,最后趨于平緩.
彈塑性;錨噴支護;統一強度理論;圍巖
在地下結構(如巷道、隧道)中,都存在圍巖變形及圍巖與支護結構相互作用問題.一方面,當洞室周圍錨有均布的徑向錨桿時,都能通過承拉限制圍巖徑向位移來改善圍巖應力狀態,而且通過錨桿承剪可改善錨固體力學參數,提高錨固體的強度,形成共同承載結構,充分發揮圍巖自承能力[1].另一方面,巖石的強度及破壞不僅與最大主應力、最小主應力有關,還與中間主應力密切相關,實驗證實中間主應力可使巖石的強度增大30%左右[2].目前,在隧道等地下結構的彈塑性分析中,通常采用Mohr-Coulom b強度理論、Hoek-B row n強度理論等單剪強度理論[3-4].然而,該強度理論忽略了中間主應力的作用,只考慮最大和最小主應力對材料強度的貢獻,導致分析結果普遍偏于保守.雙剪統一強度理論[5-7]是一種對于拉壓同性和異性,不同中間主應力效應情況下都可以適用的強度理論,并可以退化成或線性逼近于其他的各種強度理論.本文基于考慮中間主應力影響的統一強度理論,結合隧道錨噴支護對圍巖穩定性的影響,推導圍巖中基于統一強度理論錨噴支護的統一解.
1 雙剪統一強度理論
雙剪統一強度理論的表達式[5-7]為
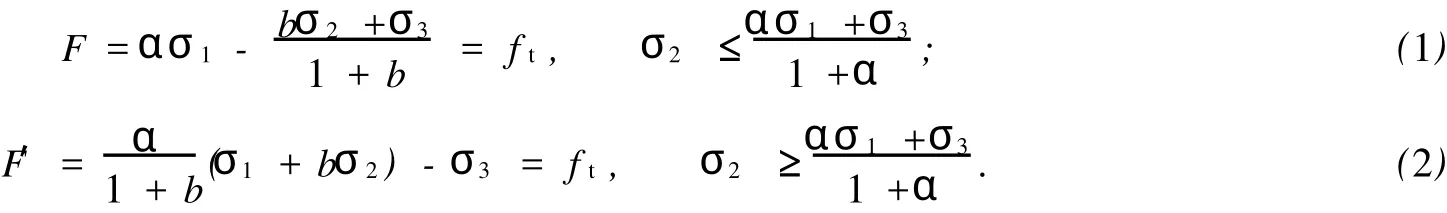
式(1),(2)中:b為強度理論參數;α為材料單軸強度抗壓比;ft為材料的單軸抗拉強度.
從上兩式可看出,統一強度理論融現有的各種強度理論于一體,已不是傳統意義上的,只適用于某一類材料的單一強度理論.如果采用單剪強度理論,就只能考慮到隧道斷面上徑向應力和切向應力的作用;而采用統一強度理論,不僅可以考慮到上述兩個應力,還可考慮到隧道軸向應力的作用[6-8].
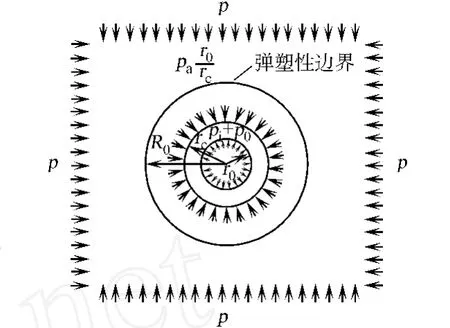
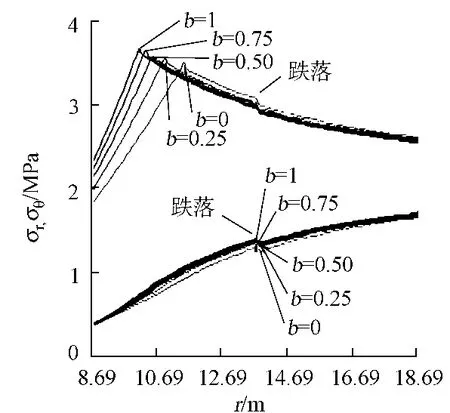
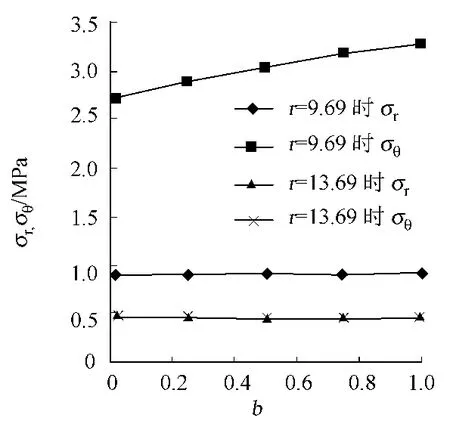
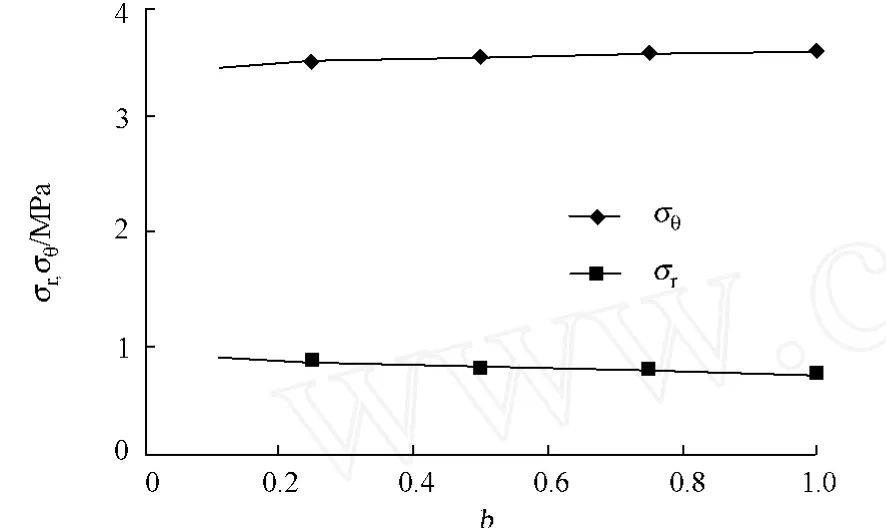
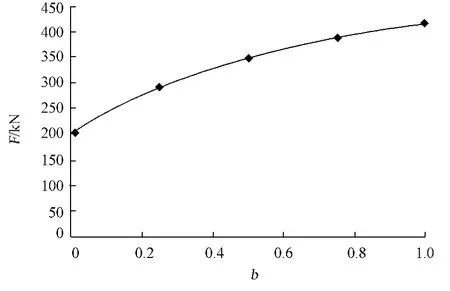
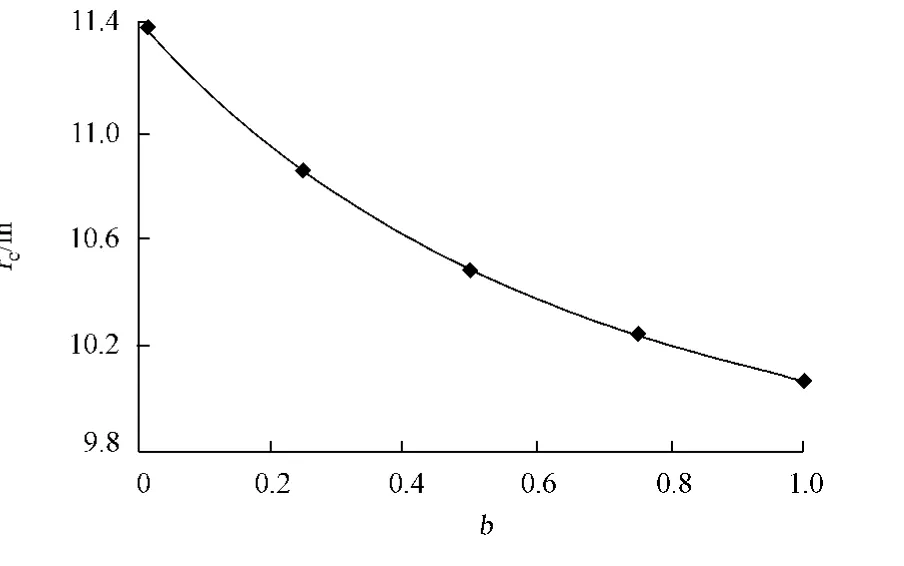
對于外凸型強度理論而言,b的取值范圍為[0,1].當b=0時,統一強度理論退化成 Mohr-Coulomb強度理論,它界定了統一強度理論的下限;當b=1時,統一強度理論退化成雙剪強度準則,它界定了統一強度理論的上限;當0 圖1 力學計算模型Fig.1 Mechanical model 靜水壓力條件下,圓形斷面隧道圍巖的彈塑性力學分析可以看成是平面應變問題,并可以認為是主應力.塑性區內的徑向應力、切向應力和軸向應力的關系為 不考慮體積力時,平面應變問題的平衡方程為 當邊界條件r=r0時,錨桿在洞壁上產生支護的附加抗力=pa+pi,將式(4)代入式(5),可得 式(6)中:rc為有錨桿時的塑性區半徑. 塑性區邊界r=rc處的應力與原巖應力p的關系為 將式(7)代入塑性條件式(4),經整理后即可得r=rc處的應力為 式(8)表明:彈塑性界面的應力是一個取決于p,C1,φ1的函數,與支護抗力pa,pi無關. 令錨桿內端點的徑向應力為σm并位于塑性區內,則在彈塑性界面上的徑向應力為 由此可得 此外,由式(4)并考慮錨桿內端的分布力,有 聯立式(10),(11),可得有錨桿時的塑性區半徑rc,即 將式(12)代入式(6),(7),可得洞壁到錨桿內端區域內的應力解析解,即 將式(11)代入式(6),(7),可得錨桿內端到彈塑性邊界區域內的應力解析解,即 錨固區內彈性區的彈性應力為 彈塑性邊界條件為 在無窮遠處有 圍巖彈性區應力及位移為 式(20)中:rc≤r≤+∞. 為求得塑性區位移up,可假定小變形情況下塑性體積不變,即ε==0.將幾何方程代入,可得 該微分方程的解為 式(22)中:A為待定系數.由彈塑性界面r=rc上變形協調,有 令彈塑性界面上的應力差為M,由式(8)可得 將彈性區及塑性區位移表達式代入(23),可得 因而,可得有錨桿時的塑性區圍巖位移,即 對于點錨式錨桿,按錨桿與圍巖共同變形理論獲得錨桿軸力,有 式(27)中:u′為錨桿外端位移;u″為錨桿內端位移為錨固前的洞壁位移,原則上應按實測值確定,也可按經驗確定;Ea,As分別為錨桿彈性模量與錨桿橫截面面積. 塑性區的應力解和位移解同上.錨固區內彈性區的彈性應力為 錨固區外彈性區的彈性應力為 由彈塑性邊界條件=可得 在無窮遠處,有=+∞==+∞=p,C′=p/2.由兩彈性區界面=+∞=p,可得 兩彈性區位移協調后可得 聯立后可得 彈塑性邊界和兩彈性區邊界分別為 因而,塑性區位移為 錨固區內和錨固區外彈性區位移分別為 實例A 8合同段大帽山隧道為泉廈高速公路擴建隧道,擴建方案在原兩洞之間新建一座4車道隧道,并將右洞擴建為4車道,形成大斷面小間距隧道群.隧道洞身最大埋置深度約為110 m,轉化為等代圓[9]后,r0=8.69 m,rc=13.69 m,C=0.2 M Pa,φ=30,p=2.12 M Pa,pi=0.3 M Pa,G=210 M Pa.經計算,錨固外端位于彈性區內,故采用錨桿錨固端位于彈性區內的計算公式,結果如圖2~8所示. 圖2 軸向(或徑向)應力與半徑的關系Fig.2 Relationship between axial(o r radial)stress and the radius 圖3 應力下降值與參數b的關系Fig.3 Relationship between stress drop and parameter of b 圖4 塑性區與錨固區半徑的關系Fig.4 Relationship between plastic zone radius and anchor radius 圖5 參數b對軸向(或徑向)應力的影響Fig.5 Parameters b influence on Influence on axial(o r radial)stress 圖6 圍巖位移與半徑的關系Fig.6 Relationship between displacement and radius for different b values 圖7 參數b與錨桿軸力的關系Fig.7 Relationship between anchor axia force and parameters of b 圖8 參數b與塑性區半徑的關系Fig.8 Relationship between parameter b and plastic zone radius 由圖2,3可以看出,圍巖應力值在rm位置有一個跌落,其中的下降值為(r0/rm)pa的下降值.當錨桿錨固外端在圍巖塑性區時下降顯著,切向應力下降值為錨固端壓力的2.5~3.5倍,徑向應力下降值為錨固端壓力的1.0~1.5倍.這主要是由圍巖極限平衡條件中的C,φ值決定;當錨桿錨固外端在圍巖彈性區時下降減小,切向應力和徑向應力下降值相等,為錨固端壓力的1/3~1/4. 由圖4可以看出,隧道圍巖塑性區半徑rc隨著錨桿錨固區半徑rm增加開始階段顯著減小,呈雙曲線函數關系;到一定階段后,rc基本無變化,呈近水平直線變化.在圍巖塑性區半徑處,錨桿長度稍微增加錨固到彈性區時,可充分發揮圍巖體的承載能力,rc有適當減小.因此,合理、經濟地選擇錨桿長度,可以有效地控制圍巖塑性區在較小的范圍內. 由圖2~8可以看出,圍巖徑向應力隨著參數b的增大而增大;切向應力在塑性區隨著參數b的增大而增大,在彈性區則隨著參數b的增大而減小;塑性區半徑和隧道周邊圍巖徑向位移隨著參數b的增大而減小;彈塑性交界處的圍巖徑向應力及切向應力均隨著參數b的增大而增大. (1)采用統一強度理論分析的錨噴支護圍巖彈塑性結果,不僅包含了以往基于Mohr-Coulomb理論等結果,并給出一系列新的結果,適用于多種的材料.(2)參數b對隧道圍巖應力場、位移場、塑性區半徑及支護反力等均有影響,因此,在隧道彈塑性分析中合理選擇參數b具有重要的意義. (3)隧道圍巖塑性區半徑隨錨固區半徑先增大而減小,之后呈近水平直線變化;在圍巖塑性區半徑處,錨桿長度稍微增加錨固到彈性區時,可充分發揮圍巖體的承載能力. (4)圍巖應力值在錨固端位置有一個跌落,當錨桿錨固端在圍巖塑性區時下降顯著,切向應力下降值為錨固端壓力的2.5~3.5倍,徑向應力下降值為錨固端壓力的1.0~1.5倍;當錨桿錨固端在圍巖彈性區時下降值減小,切向應力和徑向應力下降值相等,為錨固端壓力的1/3~1/4倍. [1]葉明亮.地下結構圍巖錨固參數的彈塑性分析[J].貴州工業大學學報:自然科學版,1998,27(1):71-77. [2]許東俊,耿乃光.巖石強度隨中間主應力變化規律[J].固體力學學報,1985,6(1):72-80. [3]于學馥,鄭穎人,劉懷恒,等.地下工程圍巖穩定分析[M].北京:煤炭工業出版社,1983. [4]王抒,張頂立.隧道軟弱圍巖相似材料的力學性能試驗[J].華僑大學學報:自然科學版,2010,31(6):680-683. [5]俞茂宏.巖土類材料的統一強度理論及其應用[J].巖土工程學報,1994,16(2):1-10. [6]俞茂宏.雙剪理論及其應用[M].北京:科學出版社,1998. [7]宋俐,張永強,俞茂宏.壓力隧洞彈塑性分析的統一解[J].工程力學,1998,15(14):57-61. [8]胡小榮,俞茂宏.統一強度理論及其在巷道圍巖彈塑性分析中的應用[J].中國有色金屬學報,2002,12(5):1021-1026 [9]李世輝.隧道支護設計新論[M].北京:科學出版社,1999. (責任編輯:錢筠英文審校:方德平) Elastic-Plastic Unified Solution of Shotcrete-Anchorage Support Surrounding Rock Based on Unified Strength Theory ZHENG Qiang,L IN Cong-mou,M ENG Fan-bing Combining the mechanical mechanism of point ancho red bolts and twin shear unified strength theory,rock stress field of surrounding,displacement field and analytical solution of plastic zone radius in circular tunnel are educed under the two-way stress in an infinite homogeneous medium,the influence of the parameterbvalue of strength theory on the features of stress and displacement distribution in the elastic and plastic zone are analyzed.Furthermore,the trend of anchor support influence on radius of plastic zone is analyzed.It′s show n that the tunnel axial stress and the parameterbof strength theory affect tunnel surrounding rock stress field,disp lacement field,p lastic zone radius and support reaction etc;the stress value of surrounding rock drops in the outside end of anchorage zone,also surrounding rock stressoutside of anchorage in the plastic zone drops more than that in the elastic zone;with increasing the anchorage area radius,the plastic zone radius of tunnel surrounding rock increases initially,then decreases,finally almost doesn′t change. plastic;shotcrete-anchorage support;unified strength theory;surrounding rock U 451.2 A 1000-5013(2011)03-0326-06 2010-12-12 林從謀(1957-),男,教授,主要從事巖石動力學和地下結構的研究.E-mail:cm lin@hqu.edu.cn. 福建省科技計劃重點項目(2007H0055);福建省自然科學基金資助項目(2006J0445)2 力學計算模型建立
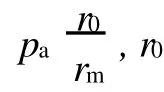
3 錨固圈位于塑性區內
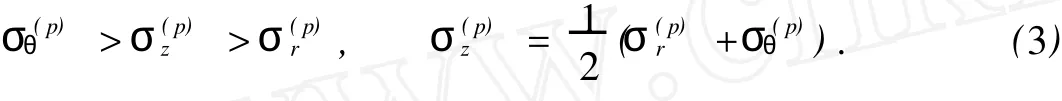
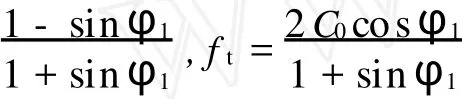

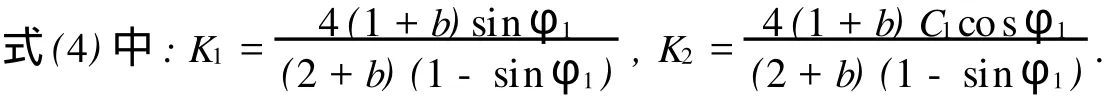



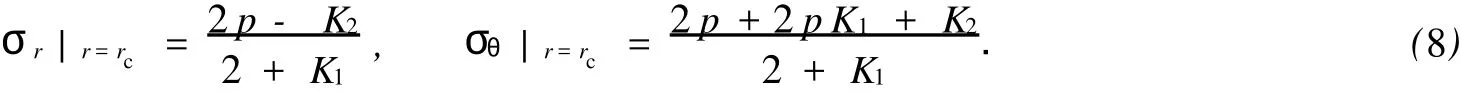


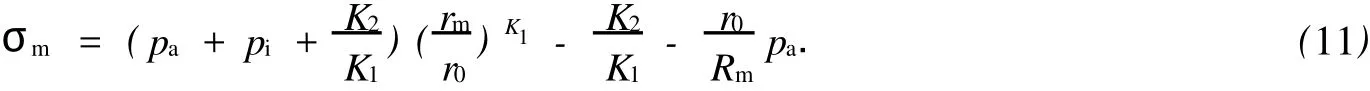
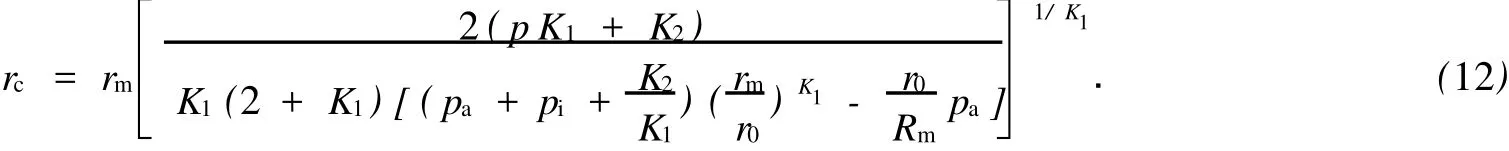
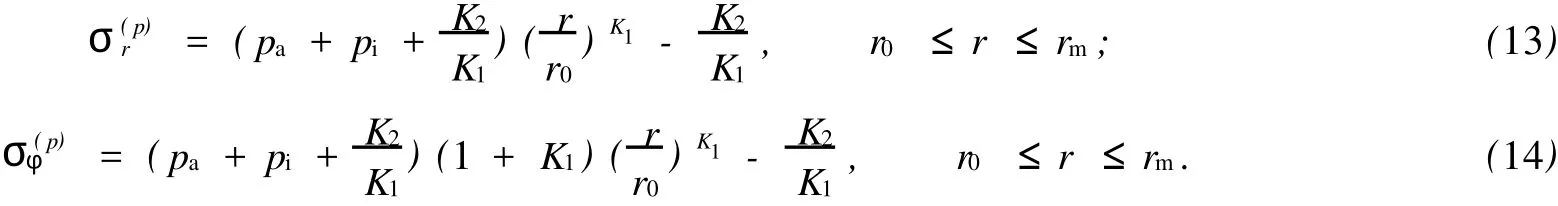

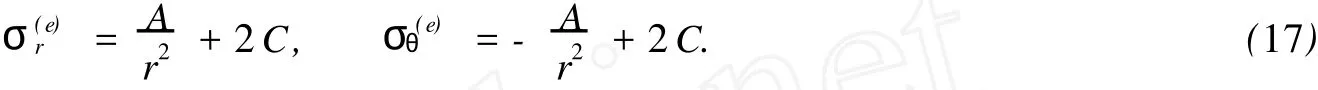
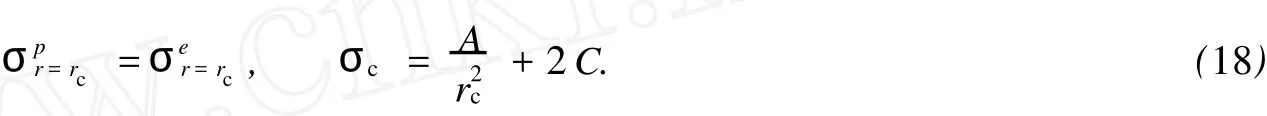

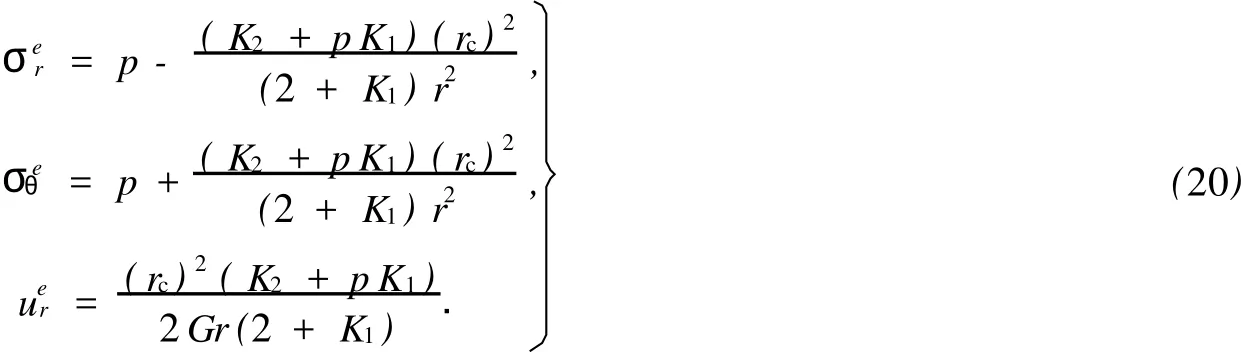



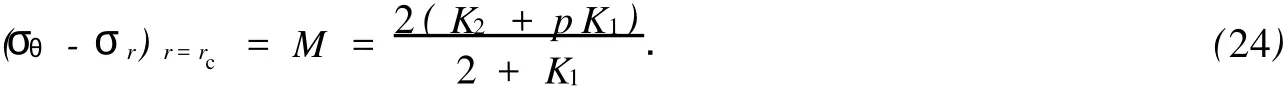
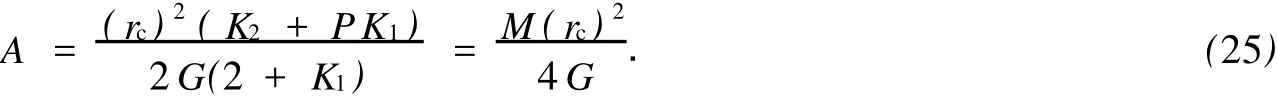
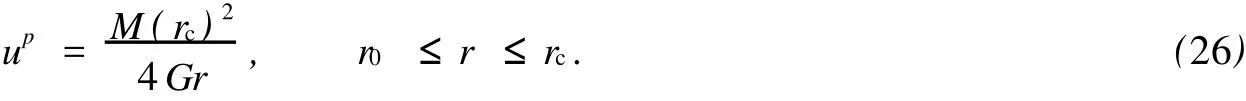
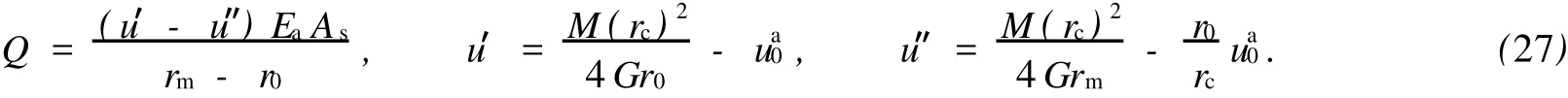
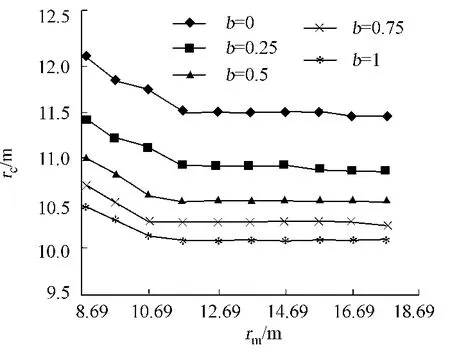
4 錨桿錨固端位于彈性區內
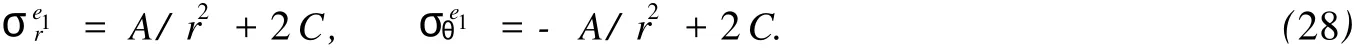




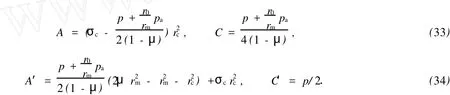
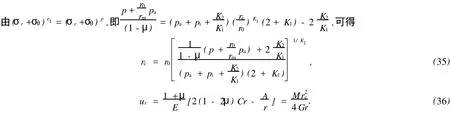
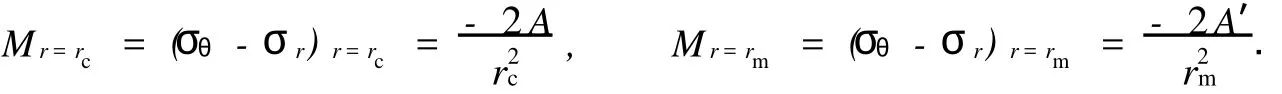
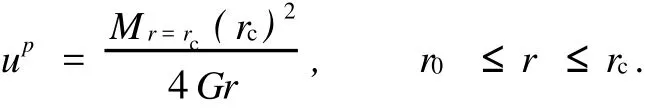
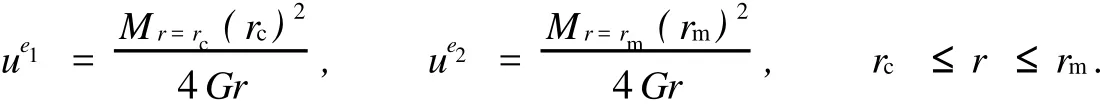
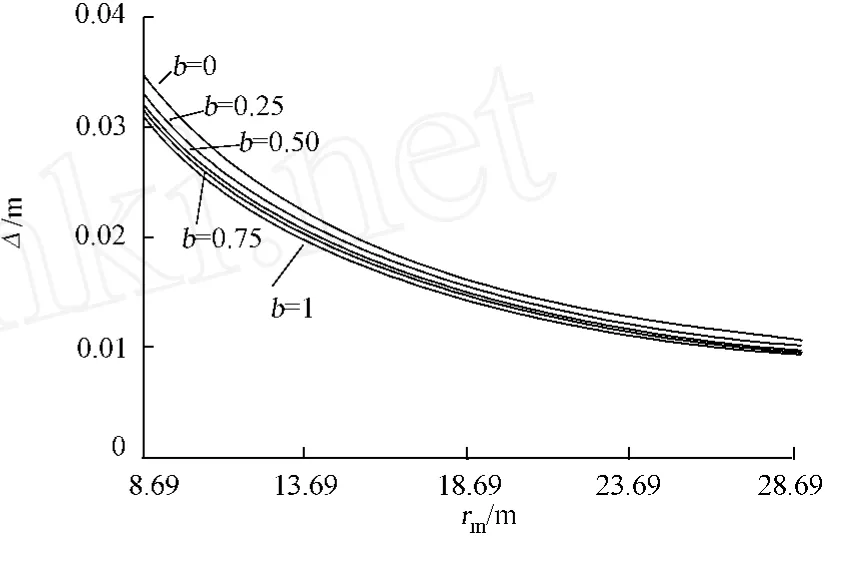
5 工程實例分析
6 結論
(Research institute of Geotechnical Engineering,Huaqiao University,Quanzhou 362021,China)

