鋼管混凝土拱橋可靠度分析

康 海 貴， 張 晶， 余 大 勝，2

（1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024；2.上海建工集團，上海 200022）

0 引 言

近年來，隨著拱圈材料強度的提高、結構體系的更新及施工工藝的改進，特別是鋼管混凝土材料在工程中的廣泛應用，拱式結構在大跨度橋梁結構中又重新煥發了青春.目前世界上跨徑最大的鋼管混凝土拱橋為四川巫山長江大橋，跨度達到460m.

然而，鋼管混凝土拱橋作為一種應用新材料的橋型，其理論研究目前還相對滯后，跟不上發展的步伐.對鋼管混凝土拱結構受力特性的研究還剛剛開始，其大長細比、曲桿、壓彎等特性與直桿的軸心受壓如柱子的受力特性是不同的；而直接套用圬工拱橋或鋼筋混凝土拱橋的計算方法也不太合理，更何況拱橋的設計理論也不完善.目前鋼管混凝土拱橋可靠度研究還處于構件可靠度階段，其體系可靠度計算還沒有進入實用階段.結構體系可靠度計算方法主要有區間估計法和點估計法.其中點估計法應用較為廣泛.本文用應力疊加法擬合成橋施工過程，運用RSM－FORM分析法計算結構體系可靠度，并深入討論在各種不利工況下結構的安全情況.

1 RSM－FORM分析法

RSM－FORM分析法綜合運用RSM（response surface method）、FEM（finite element method）、FORM（first order reliability method）計算結構主要失效模式的可靠指標，該方法包括3方面的內容：①采用RSM近似表達極限狀態方程；②采用FEM進行確定性分析；③運用FORM計算結構主要失效模式的可靠指標.因為各主要失效模式之間是串聯體系，所以可以通過點估計計算結構體系可靠度.其中①、②部分在ANSYS上運用APDL語言編寫，③部分運用FORTRAN語言實現.

Maymon［1］在商用軟件ANSYS平臺上利用APDL語言成功地實現了利用確定性分析軟件計算驗算點位置.Borri等［2］同樣在ANSYS平臺上利用它內含的優化模塊計算驗算點位置，繼而分析結構的可靠度.

Bucher等［3、4］利用 ANSYS的結構分析功能，結合響應面分析、Monte Carlo抽樣和方向抽樣方法進行結構可靠度計算，開發的SLang（CAL－reliability）在有限元程序FEAP上集成了一次可靠度算法、二次可靠度算法、Monte Carlo模擬法，既可以計算元件可靠度，也能夠分析系統可靠度.

2 鋼管混凝土橋梁體系可靠度分析

2.1 實例簡介

本次計算以某拱橋為實例，該拱橋由主橋和引橋組成.主橋由三孔不等跨中承式鋼管混凝土拱橋（主跨部分見圖1）組成，長為403.928m；拱肋布置在快車道與慢車道之間，為兩條分離式平行無鉸鋼管混凝土拱肋，中心距離為18m，主橋總寬度為32.5m.主拱計算跨徑為143.666m，計算矢高為35.017m，凈矢跨比為1／4.117.主拱拱肋由2根700mm×10mm上弦鋼管、2根700mm×10mm下弦鋼管、245mm×10mm豎斜腹桿及300mm×10mm橫聯鋼管組成等截面鋼桁架，拱肋高3.4m、寬1.8m，上、下弦鋼管內填充C50混凝土.國內首次在嚴寒地區建造鋼管混凝土拱橋，經驗不足，導致在施工過程中主橋拱軸線均勻下降，最大位移在拱頂處，下降300 mm，建模過程參見文獻［5、6］.

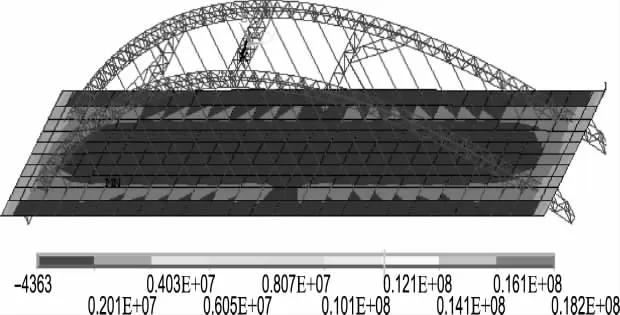
圖1 結構整體的von Mises應力等值線Fig.1 Structural von Mises stress isoline

2.2 分析模型

為真實反映橋梁施工過程、最不利活載情況及拱肋實際合攏高度，計算模型選擇如下：

（1）橋梁靜力計算依據可靠度設計理論，采用極限狀態設計方法，運用應力疊加法擬合結構的實際受力情況；

（2）車道荷載的布置分為6車道和2車道，其中2車道為荷載偏載情況，縱橋向按主跨1／2跨截面影響線、1／4跨截面影響線、1／8跨截面影響線布載；

（3）橋梁模型分為設計拱軸線和拱軸線頂部下降0.3m.

因鋼管混凝土結構是分步施工的，應力疊加法所考慮的荷載效應如下：

①鋼管鉸接時自重荷載效應S（1）；

②鋼管鉸接時溫降荷載效應S（2）；

③鋼管鉸接時混凝土自重荷載效應S（3）；

④鋼管固結、混凝土溫度收縮荷載效應S（4）；

⑤安裝橋橫梁和面板后，橋面板和橫梁自重荷載效應S（5）；

⑥汽車、人群荷載效應S（6）；

⑦橋梁的溫度下降荷載效應S（7）.

可靠度分析共定義了5個極限狀態方程，也即橋梁的5個主要失效模式，結構失效模式判斷準則如下：

（1）汽車、人群荷載作用時，跨中撓度不允許超過預拱度L／1 000，拱橋在設計時考慮恒載對橋梁拱肋撓度的影響而設計了預拱度，因此極限狀態方程中只考慮汽車、人群荷載等活載產生的撓度；

（2）主拱肋鋼管桿件的應力不能超過屈服應力，鋼管的屈服應力極限狀態方程為

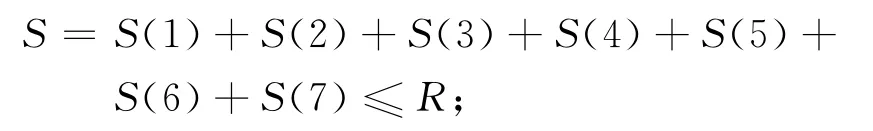
（3）主拱肋腹桿的應力不能超過屈服應力，腹桿的屈服應力極限狀態方程為

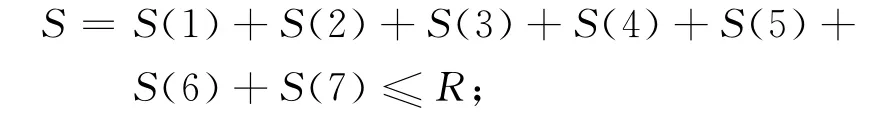
（4）主拱肋混凝土的拉應力不能超過屈服應力，混凝土的屈服應力極限狀態方程為

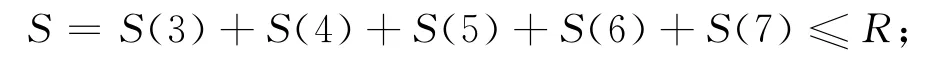
（5）主拱肋混凝土的壓應力不能超過屈服應力，混凝土的屈服應力極限狀態方程為

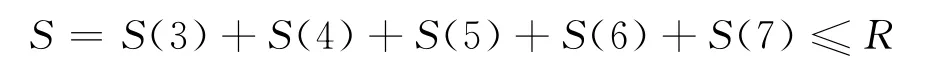
功能函數可以寫做：

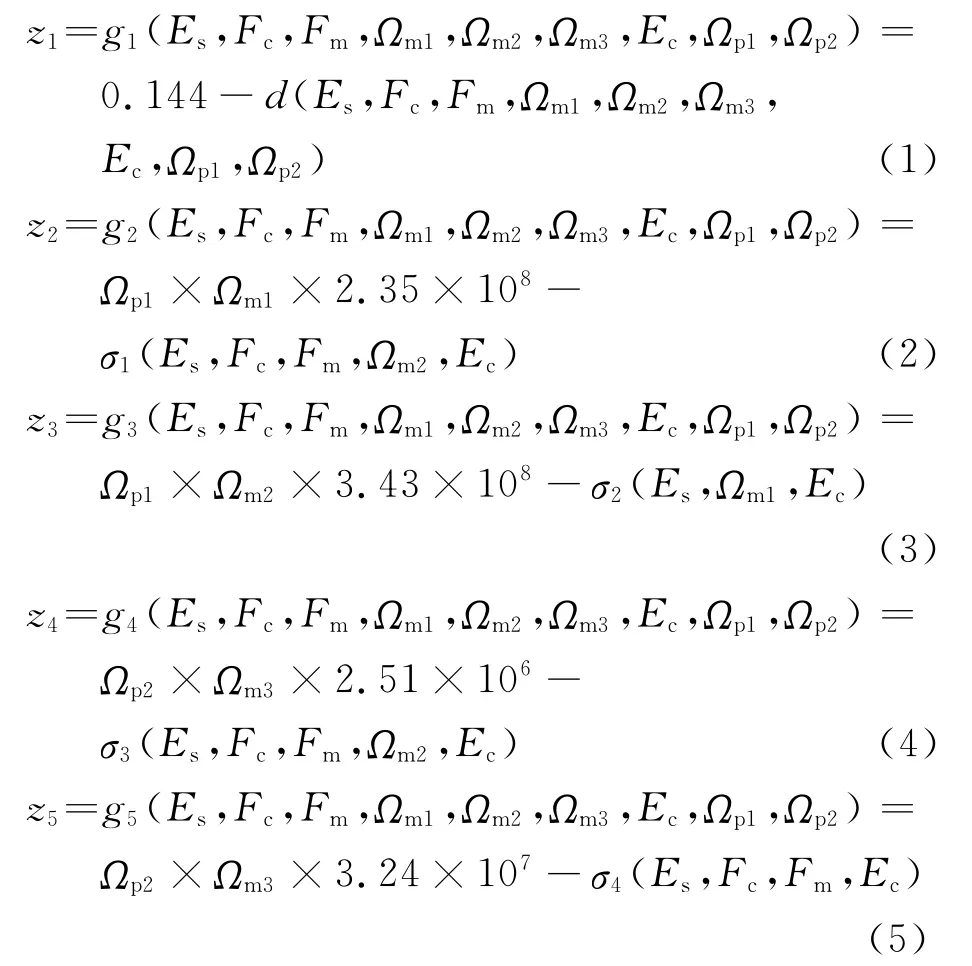
式中：d為跨中撓度，因為鋼管混凝土橋梁對于拱肋最大撓度還沒有規范，實際工程中一般鋼管混凝土拱橋取值為L／1 000；σ1為16Mn鋼的最大von Mises應力；σ2為A3鋼的最大von Mises應力；σ3為C50混凝土的最大von Mises拉應力；σ4為C50混凝土的最大von Mises壓應力.

在第2～5個極限狀態函數的定義上，采用各桿件最大應力不超過屈服應力，并沒有特別指定某個桿件，這在一定程度上反映了整個結構體系的可靠度，只不過把構件之間理想化為簡單的串聯體系.

可靠度分析是通過反復變更幾何參數、材質、荷載等分析參數實現的，其特征值的分布類型、均值和標準差取值參考文獻［7］.文中的橋梁計算，依據荷載調查和橋梁在設計、施工、使用過程中各因素的考慮，其分析參數見表1.

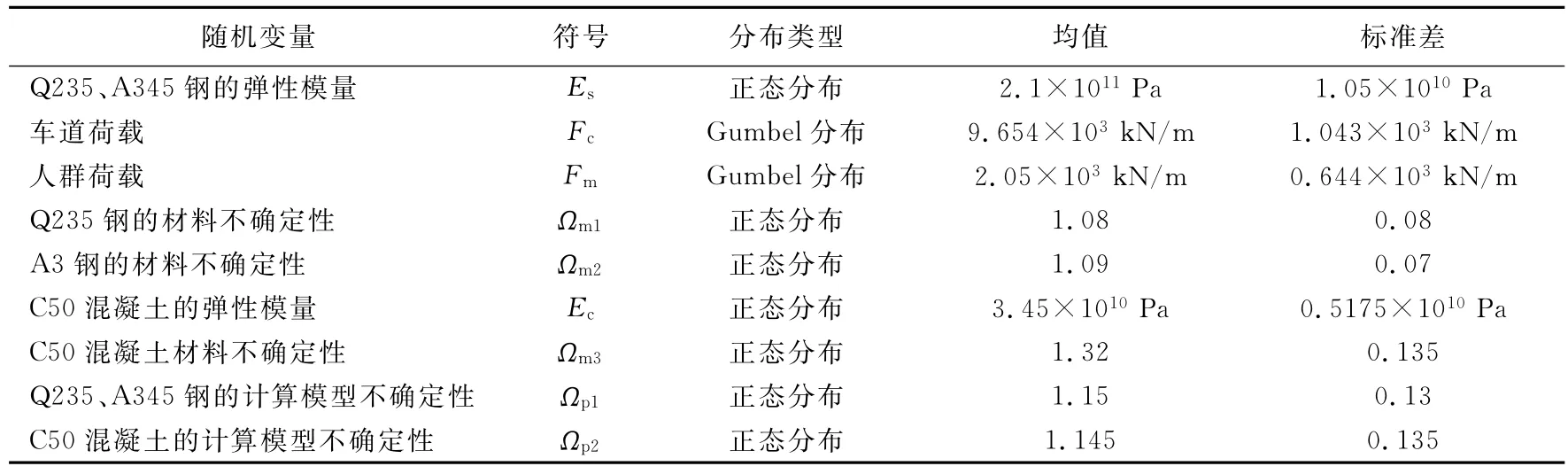
表1 大橋結構隨機輸入變量的統計特征Tab.1 Statistics of the random variables for the bridge

2.3 靜力可靠度分析

2.3.1 失效模式的可靠指標計算結果匯總 各工況下的可靠指標β見表2.

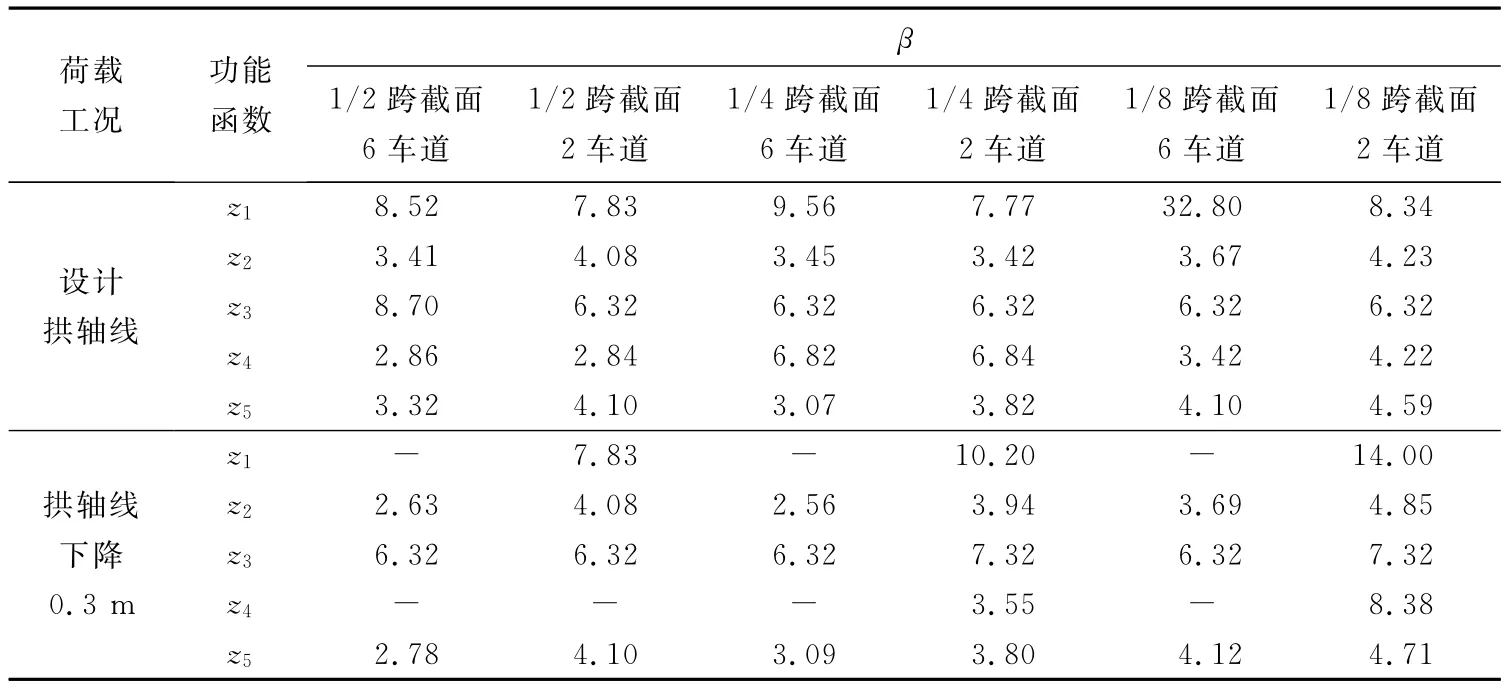
表2 各失效模式的可靠指標Tab.2 Reliability indices of different failure modes

由表2可知，橋梁的撓度較小，趨于安全；結構的最不安全環節主要集中在拱肋鋼管屈服破壞和拱肋內混凝土受壓破壞.為此有必要在兩種拱軸線情況下，對結構的主要失效模式作一比較.

2.3.2 橋梁主要失效模式可靠指標比較 由圖2、3可知，下降拱軸線的主要失效模式可靠指標與設計拱軸線相比較，更多的工況下沒有大的變化，但是在橋梁的控制截面，下降拱軸線比設計拱軸線的可靠指標低；下降后的主要失效模式為1／2跨截面6車道時的拱頂鋼管偏心受壓破壞.

2.3.3 橋梁體系可靠度 本次計算對失效模式的判斷基于靜力計算和經驗.通過計算結構主要失效模式得到橋梁體系的可靠度.各布載方式下的5種失效模式之間是串聯體系；不同的布載方式之間也是串聯體系.同一布載方式下各失效模式間的相關性非常強，相關系數接近于1.0，因此同一布載方式下可靠指標最小的失效模式可以代表該體系的可靠度情況.目前還沒有不同布載方式間相關性的統計資料，為了體現不同工況下結構的反應特點，本文考慮各工況相互獨立，即相關系數為0.整座橋梁鋼管失效的可靠指標可以用點估計法的近似計算法得到，利用串聯體系的相乘原理得到的結果能滿足精度要求.

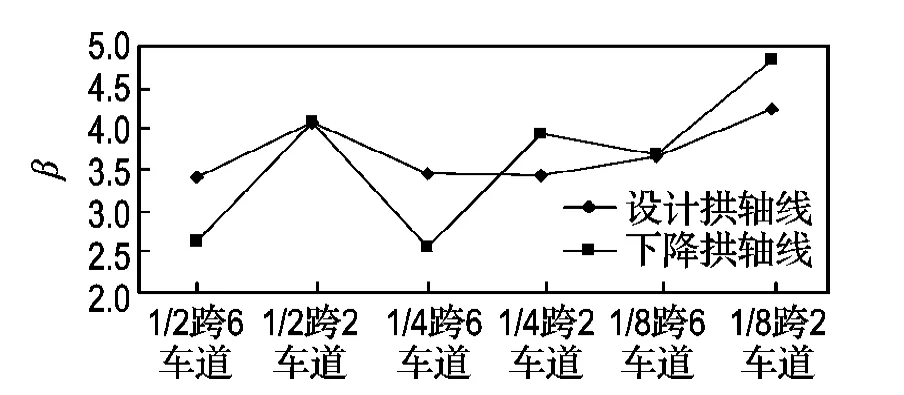
圖2 拱肋鋼管極限狀態控制截面可靠指標比較Fig.2 Comparison of steel cube reliability in the control section of main arch rib under ultimate state

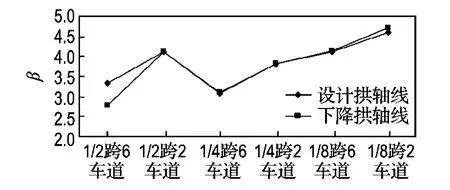
圖3 拱肋混凝土極限狀態控制截面可靠指標比較Fig.3 Comparison of concrete reliability in the control section of main arch rib under ultimate state

表3給出了2種拱軸線在正常使用荷載情況下的結構體系可靠度（Pf為失效概率）.

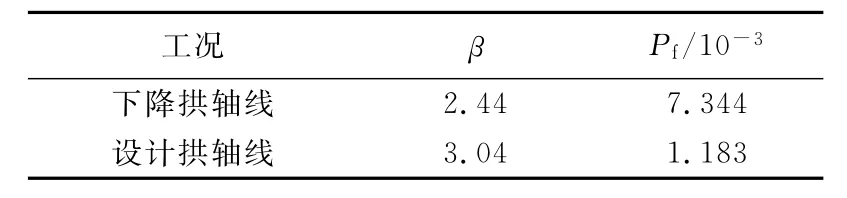
表3 橋梁體系可靠指標對照Tab.3 Comparison of the structural system reliability in arch bridge

3 結 論

（1）鋼管混凝土拱橋的拱肋撓度和腹桿極限狀態的可靠指標很大，可靠性較高；

（2）按1／4、1／8跨截面影響線布載時的失效模式都發生在拱腳處；按1／2跨截面影響線布載時，失效模式發生在拱頂拱肋處.

（3）按1／2跨截面影響線布載時可靠指標最低，是橋梁的最不利布載方式；

（4）拱軸線下降0.3m后，體系可靠指標由設計拱軸線時的3.04下降到2.44，失效概率增加了5.2倍.由此可見鋼管混凝土拱橋施工過程中精度控制的重要性.

［1］MAYMON G.Direct computation of a stochastic structure using a finite element code ［J］.Structural Safety，1994，14（3）：185－202

［2］BORRI A，SPERANZINI E.Structural reliability analysis using a standard deterministic finite element code［J］.Structural Safety，1997，19（4）：361－382

［3］BUCHER C G.Adaptive sampling — an iterative fast Monte Carlo procedure ［J］.Structural Safety，1988，5（2）：119－126

［4］BUCHER C G，BOURGUND U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7（1）：57－66

［5］張勝民.基于有限元軟件ANSYS 7.0的結構分析［M］.北京：清華大學出版社，2003

［6］張立明.ALGOR、ANSYS在橋梁工程中的應用方法與實例［M］.北京：人民交通出版社，2003：271－314

［7］中華人民共和國建設部.GB50153—92工程結構可靠度設計統一標準［S］.北京：中國計劃出版社，1992