在役鋼筋混凝土框架結構抗震性能評估

陳健云， 溫瑞智， 王寶峰

（1.大連理工大學 土木工程學院，遼寧 大連 116024；2.中國地震局 工程力學研究所，黑龍江 哈爾濱 150080）

0 引 言

結構可靠度研究目的在于使結構抗震設計理論與方法更合理.從方法上講，在役結構的可靠性分析和擬建結構沒有本質差別，但其性能、環境都經歷了一定的變化，對結構功能和使用時間的要求也可能較設計階段有所不同，這一點使現有建筑物的可靠性分析具有很多與擬建結構不同的特點.

在役結構抗力效應與擬建結構的最大區別是抗力效應的下降，已有許多學者對此進行了研究［1、2］.牛荻濤等［3］提出了服役結構抗力的非平穩隨機過程模型，建立了預測抗力平均值和標準差的數學模型.姚繼濤等［4］指出既有結構當前的抗力宜采用隨機過程概率模型描述.高小旺等［5］通過考慮鋼筋混凝土框架結構構件的各種不確定因素來綜合推斷鋼筋混凝土框架結構層間屈服和極限變形的概率統計特征.

由于在役結構已經服役了一段時間，對在役結構進行抗震安全性評估所采取的地震動有不同的確定原則.目前常用方法有等烈度方法（對在役結構后役期抗震安全性評估時采用當地的設防烈度）、等超越概率方法（無論在役結構后役期多長，始終保持相同的超越概率）［6］.

歐進萍等［7、8］綜合考慮了地震烈度的隨機性、地震動的隨機過程性及其動力效應，討論了相應于設計基準期內結構隨機地震作用的統計參數和概率分布.本文在此基礎上，充分考慮在役建筑物的實際特點，以及所處的實際環境，進一步考慮建筑物在服役一段時間以后抗力和地震作用隨時間的變化，對在役結構進行抗震性能評估，并比較其中的差別.

1 在役建筑物地震動參數

評估烈度是為了確定在役建筑物抗震評估用地震作用而規定的地震烈度，相當于設計時的“設防烈度”.在役結構的評估可以按照抗震風險評估中等超越概率原則確定抗震設防標準，以確保結構在后續使用期內與原設計在設計基準期內具有同等的風險水平.在役建筑物的評估基準期Ta（即評估荷載基準期）可定義為后續使用期內小震烈度對應的重現期，它是一個隨后續使用期變化的量：

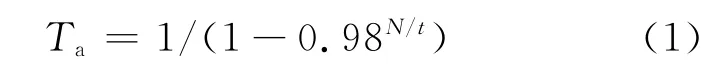
式中：N為設計使用期（a），t為結構的后續使用期（a）.

由設計基準期內地震烈度的概率分布函數可推得任意評估基準期Ta內超越烈度i的概率，以基本烈度I0表示，任意評估基準期Ta內超越烈度i的概率為

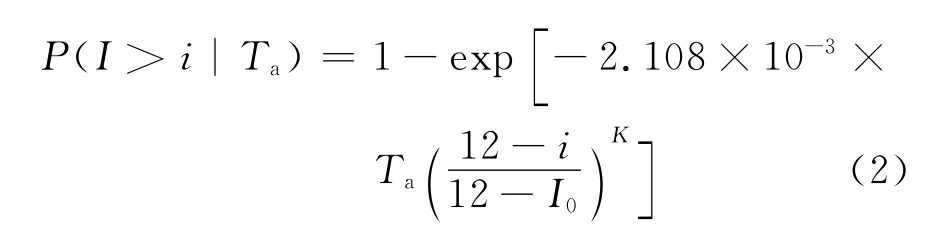
利用上式可以求出某個場地在給定超越概率條件下任意評估基準期內的地震烈度i.

高小旺等的研究統計表明，在50a設計基準期內地震烈度較好地符合極值Ⅲ型分布，分布函數為［9］

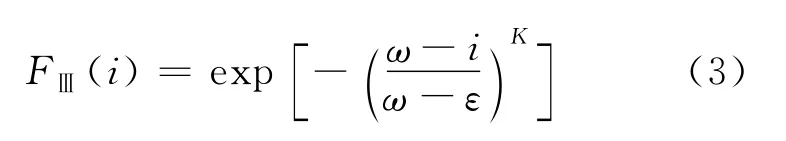
其中ω＝12，為烈度上限值；ε為眾值烈度，在一定時期內超越概率為1－e－1＝0.632的烈度；K為形狀參數，確定方法及取值見文獻［10］.

地震影響系數最大值αmax與地震烈度的關系可表示為

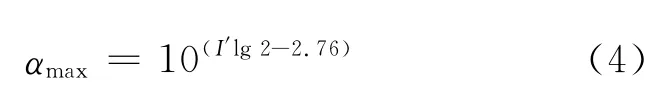
式中：I′為與后續使用期內的評估烈度相對應的眾值烈度或罕遇烈度.

在地震工程中地震動空間分布一般是用對應于基巖的地震動參數衰減關系得到的，針對場地條件對設計地震動的影響，李小軍［11］給出了如下調整公式：

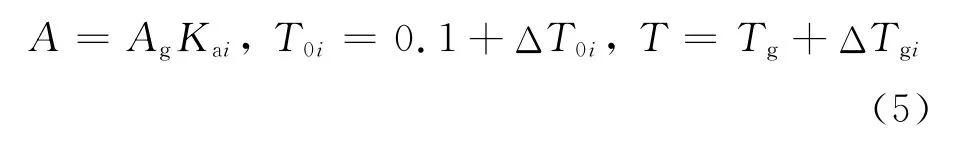
式中：Ag、Tg代表基巖場地的地震動反應譜參數，Kai、ΔT0i和ΔT是不同場地的反應譜調整系數.具體值參考文獻［11］.

2 基于概率Pushover分析的結構體系抗震可靠度評估

2.1 在役結構的抗力衰減模型

隨時間變化的抗力不確定性可分為材料性能的不確定性、幾何參數的不確定性和計算模式的不確定性.本文通過不同發生概率的抗力曲線（能力曲線）表示結構抗力的隨機性.

抗力隨機過程模型可表示為

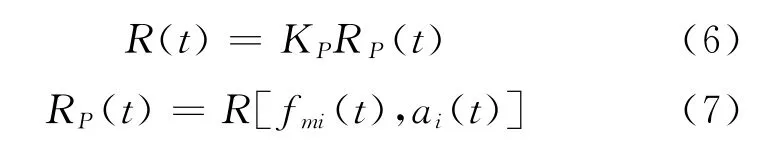
式中：KP為描述計算模式不確定性的隨機變量；RP（t）為結構的計算抗力，由Pushover分析確定；fmi（t）和ai（t）為第i種材料的性能和幾何參數，是時間t的函數，本文指的是混凝土和鋼筋這兩種材料的時變規律［12、13］.

通過結構可靠度的靈敏度分析，可得到影響結構抗力的m個主要隨機影響因素Ai（i＝1，2，…，m）［14］.將主要影響因素Ai的概率空間離散為n個子空間，離散事件Aij（j＝1，2，…，n）出現的概率為P（Aij），在影響參數為確定性的aij時，aij對應結構體系抗力的概率為P（aij）.在分析過程中如果分別代入結構使用期為t時的結構抗力參數，則可求出結構體系在使用期為t時的抗力.

由于在役建筑物的抗力隨服役時間變化，本文采用非平穩隨機過程模型描述在役建筑物的抗力，并假定在役建筑物的抗力服從對數正態分布.任意時刻t抗力R（t）的概率密度函數可以表示為

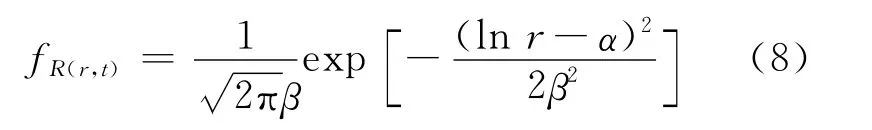
其中α和β為參數，由抗力R（t）的平均值和標準差σ確定.

鋼筋混凝土框架結構層間屈服和極限變形的概率統計分析，需要收集大量的試驗資料，或考慮各種隨機因素，針對不同參數取值進行大量計算分析得到不同破壞狀態變形指標等參數的概率統計特征［5］.

在目前的研究水平下，考慮目前多因子模型研究的廣度和深度的不足，加上問題本身存在的客觀復雜性、困難性，本文以指數型模型為基礎，對抗力的衰減考慮結構所處環境中各種因素的影響，從總體上進行折減.

文獻［15］指出對于抗力均值的衰減模型，采用3種已有模型得到的計算結果將基本吻合，抗力均值采用的指數型衰減函數表達為［15］

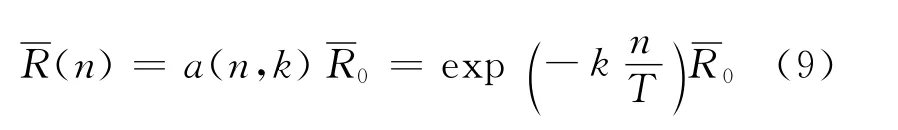
衰減函數中a（n，k）可視為以a為單位的結構抗力的確定性衰減函數，可通過設計使用年限T與已使用年限n來確定，參數k＝－lna（T），一般取指初始結構構件抗力的均值指在役結構構件當前抗力的均值.

假設抗力衰減函數的方差隨時間呈線性增長，設新建結構的方差為σ（R0），既有結構當前的方差為σ（R（n）），且σ（R0）≤σ（R（n）），則任意時間n的σ（R（n））可按線性插入法確定［2］：

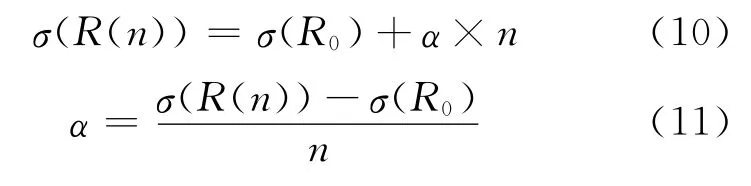
2.2 隨機需求譜模型

Pushover分析方法的需求譜曲線由規范反應譜確定，本文通過隨機地震作用模型描述需求譜曲線的隨機性.

確定性烈度下的隨機地震作用符合極值I型分布，概率分布函數表示為

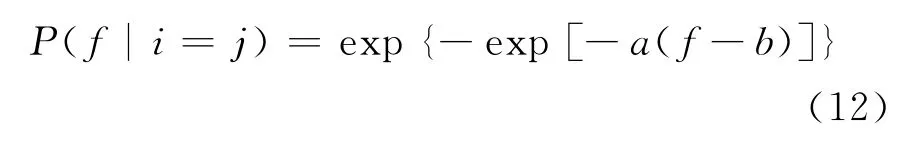
其中分布參數a、b按下式計算：

確定性烈度下的隨機地震作用的均值和變異系數分別表示為

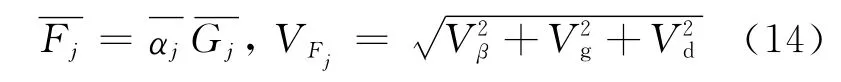
2.3 在役結構可靠度極限方程

以結構總體破壞指標建立的結構可靠度分析極限狀態方程為

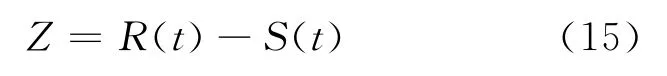
式中：R（t）是結構抗力；S（t）指荷載.

結構體系的失效概率按下式求得：

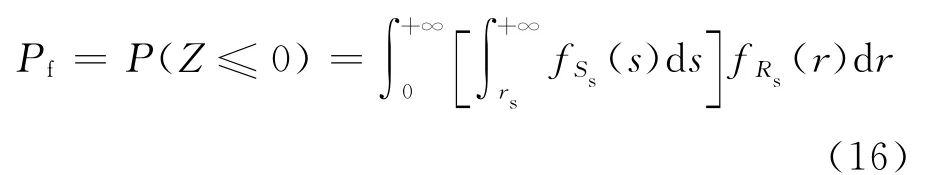
3 計算實例

某市一9層鋼筋混凝土框架結構，設計基準期是50a，采用三跨平面計算模型，邊跨4.2m，中跨6.6m，建筑物高度為第1層4.5m、第2～8層3.3m、頂層4.2m.構件幾何尺寸、混凝土等級如表1所示.該結構中梁柱的縱向鋼筋為Ⅱ級，箍筋為Ⅰ級.建筑地點設防烈度為7度、Ⅱ類場地，設計地震分組為第1組.在2～9層上每個節點有豎直向下作用的集中恒荷載7.50kN；2～8層的邊跨A－B、C－D作用分布荷載－26.80kN／m，9層是－30kN／m；2～9層的中跨B－C作用－5.25kN／m；2～8層中跨的1／3和2／3處作用集中荷載－9.64kN，頂層是－10.8kN.

表1 結構構件參數Tab.1 Structure component parameters mm

3.1 基于地震動等超越概率的不同后續使用期內結構地震動響應

通過Pushover方法對結構在不同評估烈度所對應的多遇和罕遇地震下結構在不同后續使用期內的地震反應進行了計算，最大層間位移角θmax的計算結果如表2所示.

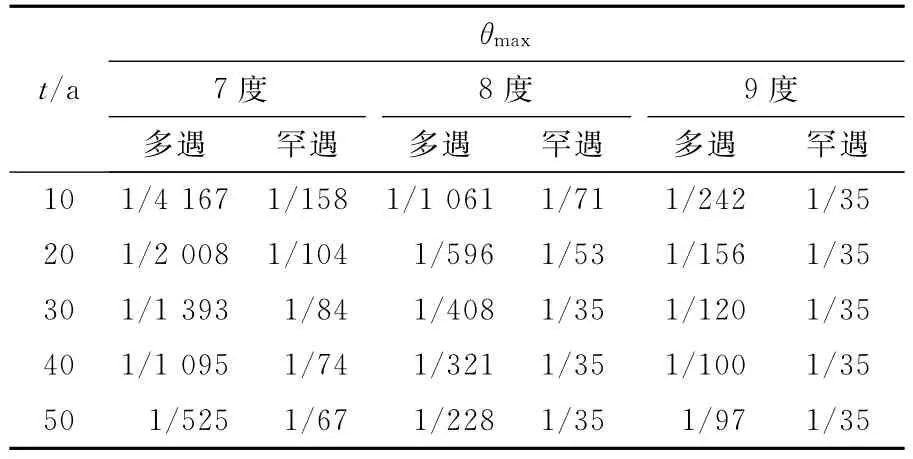
表2 不同后續使用期內性能點的最大層間位移角Tab.2 The maximum inter－story drift angle at various re－services term of the performance point

從表2中可看出，盡管隨著使用年限的增加，結構的抗力不斷衰減，但是按照等超越概率原則所承受的地震動也降低了，因此隨著后續使用年限的縮短，性能點的位移反應反而不斷減小.

從分析結果中可以看出：

（1）對應于7度設計烈度條件下，多遇地震作用下樓層內最大彈性層間位移的最大值小于規范中規定的彈性層間位移角限值1／550，滿足規范中的要求，說明結構隨著后續使用期的縮短，仍然滿足規范規定的抗震變形驗算；罕遇地震下結構薄弱層處的彈塑性層間位移的最大值仍然小于規范中規定彈塑性層間位移角限值1／50，滿足罕遇地震下薄弱層處的彈塑性變形計算.

（2）對應于8度設計烈度條件下，多遇和罕遇地震作用下結構早期基本不滿足規范中的層間位移角限值，隨著后續使用期的縮短結構的層間位移逐步減小，后20a內滿足規范規定限值，這是因為雖然結構抗力隨著使用年限減少逐漸降低，但是結構遭遇的地震作用也是同時相當于減小的.

（3）對應于9度設計烈度條件下，多遇地震作用下彈性層間位移大于規范限值，但結構仍處于“中震可修”的狀態；在9度罕遇地震作用下，彈塑性層間位移值基本保持不變，結構處于完全毀壞狀態.

3.2 結構體系的失效概率和易損性曲線

本文分別針對等烈度和等超越概率兩種情況對結構的失效概率進行了比較研究，所采取的震害等級劃分如表3所示，其中θe為規范中彈性層間位移角限值.不同破壞等級對應的易損性曲線如圖1所示.經計算得出的抗力時變函數隨著后續使用期的減少表現出的衰減系數如圖2所示.

表3 結構的震害等級劃分Tab.3 Damage levels of structures

比較圖3、4可以看出：

（1）按等超越概率方法計算的各個破壞狀態下的失效概率，除對應于9度設計烈度情況下的輕微破壞和中等破壞的易損性隨后續使用年限有增大趨勢外，其余情況下基本上是隨著后續使用年限的減小而減小的，且隨著破壞狀態的加劇失效概率減小的趨勢逐漸變緩.但是按等烈度方法計算的各個破壞狀態下的失效概率，趨勢正好相反，大致是隨著后續使用年限的減小而增大.

（2）等烈度方法計算出的各個破壞狀態下的失效概率大于等超越概率方法計算的結果，考慮抗力衰減與按等烈度方法計算的各個破壞狀態下的失效概率結果最大，抗力不衰減與按等超越概率方法計算的結果最小，本文采用的考慮抗力衰減與按等超越概率方法計算的結果處于中間位置，因為等烈度方法實際上是把在役結構評估基準期等同于結構設計基準期，當在役結構后役期小于結構設計基準期時，結構的抗震風險水準將會提高，年超越概率同樣得到提高；而等超越概率方法是無論在役結構在役期或者后役期有多長，它始終保持相同的超越概率，實際上它保持的是與設計結構相同的抗震風險水平.

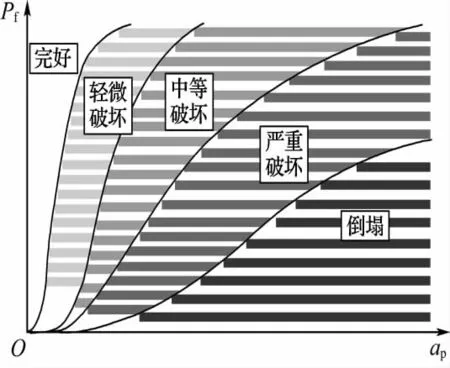
圖1 不同破壞狀態的易損性曲線Fig.1 The vulnerability curves under different damage states

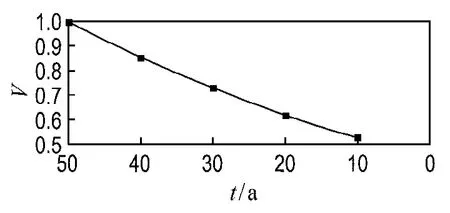
圖2 抗力時變曲線Fig.2 Time－varying resistance curve

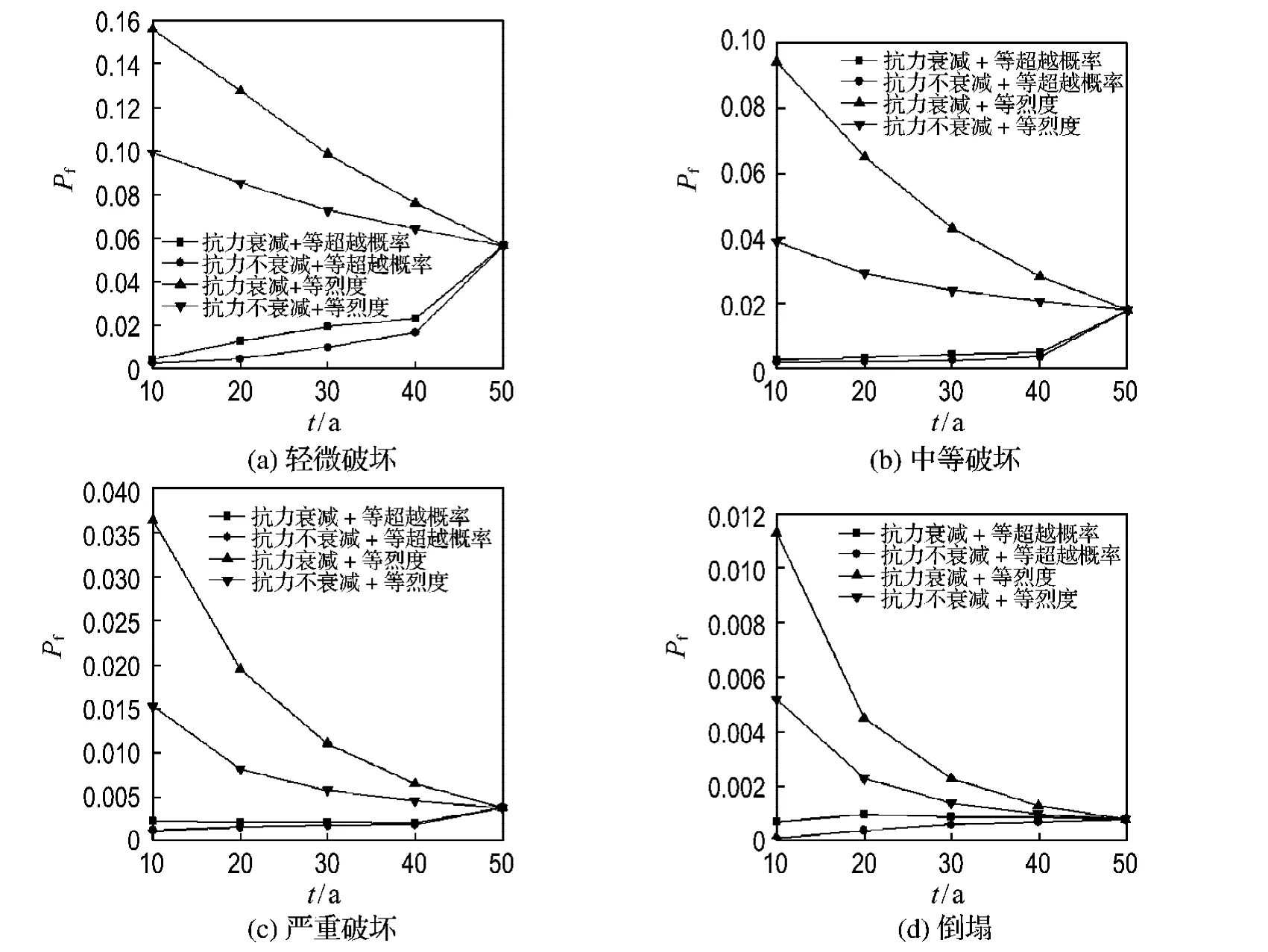
圖3 7度地震下各組合反應不同破壞狀態的比較Fig.3 The comparison of the different damage states with 7degree earthquake response of different combinations

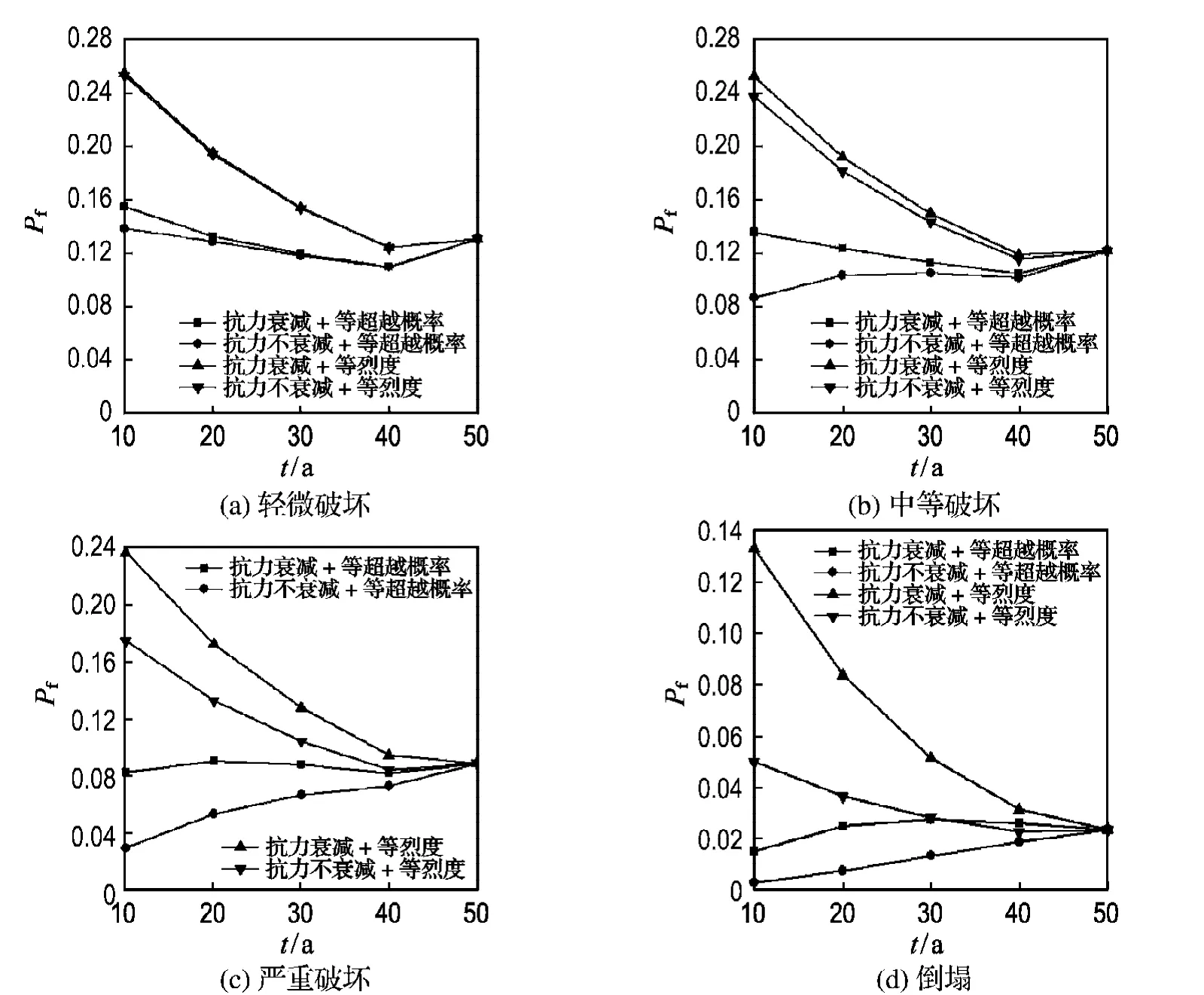
圖4 9度地震下各組合反應不同破壞狀態的比較Fig.4 The comparison of the different damage states with 9degree earthquake response of different combinations

4 結 論

（1）通過結果數據分析比較了等超越概率方法和等烈度方法的不同，并且結合是否考慮抗力的衰減，對4種不同的分析組合進行了比較，得出的結果可作為以后對建筑結構抗震評估的參考依據，但是抗力衰減是很復雜的，本文與實際情況相比對其進行了很大的簡化，因此如何考慮實際結構的具體情況，對在役結構進行更為準確的計算，仍需更多努力.

（2）在對在役結構的抗震性能評估中，應充分考慮場地土對地震動參數的影響，并據此做出適當的調整，同時要充分考慮到在役結構的后續使用期小于設計使用期這一實際情況，使得分析結果更加接近實際情況.

［1］貢金鑫，趙國藩.考慮抗力隨時間變化的結構可靠度分析［J］.建筑結構學報，1998，19（5）：43－51

［2］張耀華，王鐵成，楊建江.考慮抗力時間衰減既有結構可靠度分析［J］.山東農業大學學報，2006，37（3）：429－435

［3］牛荻濤，王慶霖，董振平.服役結構抗力概率模型及統計參數［J］.西安建筑科技大學學報，1997，29（4）：356－359

［4］姚繼濤，劉金華，吳增良.既有結構抗力的隨機過程概率模型［J］.西安建筑科技大學學報，2008，40（4）：445－449

［5］高小旺，沈聚敏.鋼筋混凝土框架房屋不同破壞狀態的抗震可靠度分析［J］.建筑科學，1993（1）：3－10

［6］丁伯陽，趙 冬，李通坤，等.在役結構后役期的設防烈度探討［J］.地震學報，2005，27（6）：677－681

［7］歐進萍，段宇博，劉會儀.結構隨機地震作用及其統計參數［J］.哈爾濱建筑工程學院學報，1994，27（4）：1－10

［8］歐進萍，侯綱領，吳 斌.概率Pushover分析方法及其在結構體系抗震可靠度評估中的應用［J］.建筑結構學報，2001，22（6）：81－86

［9］高小旺，鮑靄斌.地震作用的概率模型及其統計參數［J］.地震工程與工程振動，1985，5（1）：13－22

［10］李亞琦.中國地震危險性特征區劃［D］.哈爾濱：中國地震局工程力學研究所，1999

［11］李小軍，彭 青，劉文忠.設計地震動參數確定中的場地影響考慮［J］.世界地震工程，2001，17（4）：34－41

［12］牛荻濤，王慶霖.一般大氣環境下混凝土強度經時變化模型［J］.工業建筑，1995，25（6）：36－38

［13］牛荻濤，王慶霖，王林科.一般大氣環境混凝土中鋼筋銹蝕量的估計［J］.工程力學，1997，14（1）：92－99

［14］王春光，石永久，王元清，等.結構可靠度計算中的敏感性因素分析［J］.清華大學學報（自然科學版），2000，40（6）：108－111

［15］李桂青，李秋勝.工程結構時變可靠度理論及其應用［M］.北京：科學出版社，2001