數學解題思維與解法發現的途徑

廣 東 葉國強

數學解題思維與解法發現的途徑

廣 東 葉國強

掌握思考方法是學習數學的重要環節，本文圍繞數學常用思考方法展開論證，揭示解題規律。

解題途徑；細分；變換；試猜；逼近

蘇聯教育家加里寧說過：“數學是思維的體操。”這確實至理名言。學好數學，能使思維敏捷、清晰、精細。數學的訓練價值在何處，其思維規律是什么？不少人的做法是“大量運動”訓練，認為做題千萬，奧妙自得，無須問什么規律。這當然談不上科學性，“熟讀唐詩三百首，不會作詩也會吟”，乃是找不到“規律性”時不得已而為之，時至今日，似乎已到了大力研究數學思維規律，科學地設計“思維體操”的時候了。下面就數學解題的思維過程及解法發現的途徑進行探討。

解題思維過程究竟是什么樣才最為合適？許許多多人都在思考與研究這個問題。蘇聯著名的數學家C.A亞諾夫斯卡婭對“解題是什么”的回答驚人的簡單：“解題就是把習題歸結為已經解過的問題”，就是說，要努力把非基本題分解成或歸結為基本題。蘇聯心理學家魯賓斯坦認為，“人們解題是一個改編習題的過程”。在這個過程中，通過綜合習題條件和要求之間的聯系，對這些條件和要求進行不斷的分析、綜合與概括的過程。世界著名的數學家波利亞指出，要構想出一個解題計劃的思路，經常有用的辦法是：不斷地變換你的問題，“試驗對問題作各種修改。我們必須一再地變化它……直到最后成功……”。解決數學問題的思維過程，可以認為就是不斷變換問題的過程，從而也是一種試錯的過程。

下面就以“細分”、變換”、“試、猜”、“逼近”為綱，具體分析數學解題法發現的一般途徑。

一、化解與疊加

“化整為零”，“化大問題為小問題”，“分而治之”，歷來是各方明智之士解決困難的訣竅之一，也是我們在數學解題中經常使用的一種思想方法。

具體地把一個數學問題分解開來的方法，又有兩大類型：一是把一個較困難的問題，分解成一組系列題，這組題目中，前一個題的結果往往直接影響到后一個題的解答：通常是后一個題的一個或幾個已知條件；二是把一個大問題，分割成有并列關系的幾個題，這幾個題目之間，在解決方法上可能會有某種相似或聯系，但沒有前一個題的結果，后一個題一般仍然可以獨立地予以解答。前者的關鍵是發現幾個解題理論中的所謂中途點；后者的要津，是找到一個或幾個比較容易處理的所謂導引特款（波利亞）。

（一）中途點與縱向分解

其意義和實質在于：通過縱向地“分解大問題為小問題”，用兩個或多個較簡單的問題“串聯”來代替一個難題。找到有希望恰好落在通向“終點”的道路上的中途點，能大大地縮小解題的嘗試范圍。

（二）導引特款與橫向分解

所謂導引特款，通常指的是對于待解決的問題，可以起導引作用的某特殊情形。波利亞認為，“從一個或幾個導引特款出發，利用特殊情形的疊加去得出一般問題的解”，是數學解題中的一個有用模式。疊加，這里是把各種特殊情形采用適宜的方式組合起來的意思。教科書上圓周角定理的證明是這個模式的一個典型例子。

二、等價與映射

一個數學問題，往往具有種種不同的表達形式，相應地也有種種不同的處理方法。由于這些處理方法的難易程度各不同，這樣，這些表達形式的難易就會因人而異。因此，要解決一個問題，對不同的人，就在于選擇一種恰當的表達形式，以便利用他自己所熟悉的工具。從這種觀點來看，把一個問題變換成種種等價形式，或映射到另一個領域中去，勢必將大大地增加這個問題的可能性。下面舉一些例子加以說明。

1.命題的等價變換。找到命題的等價條件，通過恒等變換是常用的手法。

三、試探與猜想

偉大的數學家、教育家波利亞在《數學與猜想》一書中指出：“數學家的創造性工作成果是論證推理，既證明；但是這個證明是通過合情推理，通過猜想而發現的，只要數學的學習過程稍能反映出數學的發明過程的話，那么就應當讓猜測、合情推理占有適當的位置”。他強調教學必須為發明作準備，或至少給一點發明的嘗試，他向教授呼吁"讓我們猜想吧！"這是應該引起我們重視的問題。在數學教學中適當反映數學的發現過程，培養學生直覺思維，學會通過合情推理，提出猜想，這是現代數學教育工作中的重要任務。

1.觀察發現

許多數的性質，是由觀察發現的，著名的哥德巴赫猜想，就是在觀察3+7=10,3+17=20,13+17=30后發現這三個式子都是兩個奇素數之和為偶數，進而在觀察最小的兩個奇素數之和3+3=6，再觀察超過6的偶數8=3+5,10=3+7=5+5,12=5+7,14=3+11=7+7，……從而提出大于4的偶數都是兩個奇素數之和的猜想。可見觀察是發現問題的第一步，觀察力是發現能力的基礎。在數學教學中我們贏盡可能給學生以觀察發現的機會，如講異面直線時，可以讓學生觀察所在教室的墻的交線的位置關系，在講用祖衡原理求證球的體積之前，讓學生觀察實驗，將半球裝滿水或砂子，倒入等低同高的圓柱體內，讓學生發現圓柱體內水面高度，恰好是圓柱體內的高的，在觀察的基礎上，猜想兩個半球體積是圓柱體積，即然后再證明。

2.合情推理的訓練

合情推理的方法是多方面的，沒有固定的標準。常用的有歸納法，類比法，特殊化和一般化的方法。

（1）歸納推理

歸納法是對某些單個的、特殊的食物進行分析比較，從中歸納出共同特征和規律，提出猜想，發現解決問題的方法，發現新的知識。歸納推理在數學的起源和發展中都起了重要作用，如微積分的建立是牛頓和萊姆尼茨將十七世紀以來許多數學家研究的成果，如求變化率的速率，拋線的切線，極值問題歸納為微分，而把處理從加速度求距離，求曲線長等歸納為反微分問題，這是歸納發現的例子。在數學史上提出猜想再證明的例子屢見不鮮。

為了培養學生歸納發現的能力，在數學中應盡可能讓學生進行歸納發現活動。例如在學習一元二次方程根與系數的關系時，可讓學生解幾個具體的方程。如

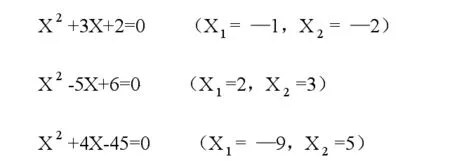
引導學生在觀察基礎上歸納發現根與系數關系。再如再解一些比較抽象的問題的時候，可以從具體例子開始研究運用歸納推理，尋求一般解法。在教學生歸納方法的時候，要注意培養學生科學的態度。首先要有探索真理的勇氣，大膽提出猜想，同時要堅持實事求是的態度，如果發現猜想不符合實際，就要有勇氣修正它，沒有充分理由，不輕易放棄原有的猜想。要通過不斷實踐檢驗猜想，從理論上證明猜想的正確性。

（2）類比推理

由于時差的緣故，我越來越不喜歡去美國出差試車，而且在生理和心理層面，潛意識里越來越擔心試駕那種主打舒適豪華氣質的車型，因為一旦被新車的從容舉止所感染，我很容易犯困。而且試車地點越是陽光明媚，試駕行程越是不緊不慢，我就越容易就范。尤其是在當地時間的下午，相比在駕駛席上安逸地掌控車輛，我更樂于在副駕駛或者后排座椅的舒適區里被時差掌控，把車輛和手機調成靜音狀態，美美地睡上一覺。

通過類比可以發現新知識、新方法。古代魯班師傅在山上砍樹被野草劃破皮膚后，他發現野草邊緣上有許多鋒利的鋸齒，類比設想發明了木工的鋸子。數學的發現中也常從類比開始。在類比中要抓住事物的本質屬性，找到他們內在的聯系才能進行類比，如平面圖形和空間圖形有相似的特征，平面上兩條直線不能圍成一個有限圖形，三條直線可以圍成一個三角形；在空間將直線換成平面，出現三個平面不能圍成有限圖形，四個面可以圍成一個四面體。從兩者以數目最少的簡單分界為元素所圍成的圖形看，三角形與平面的關系、四面體與空間的關系是一致的，存在類比關系。可以從平面圖形的性質類比猜想立體幾何的性質。在類比中一定要向學生說明，這是合情推理的一種猜想，它的正確性一定要經過證明才能成立。

（3）從特殊化到一般化的方法

在尋找較大一類范疇的問題的解法遇到困難時，可以把這一范疇縮小到比較特殊的情況，從而可以發現一般情況的解法。即從對象的一個給定的集合，轉而研究包含在這集合的"特殊化"的探索法，由于矛盾的普遍性寓于特殊性中，通過特殊化，可以打開解決一般問題的思路。這種特殊化方法是我們探求復雜問題的解法的一種有力的手段。如從任意n多邊形引進一個限制（所有邊和角相等），即對正n邊形進行研究，進而對n=3的情況，即等邊三角形進行研究。特殊化的發現的好處是：1從邏輯上看，概念的外延縮小，則它的內涵增多，研究起來比較容易；2從認識論上看，復雜的問題經過特殊化后，由淺入深，比較符合人的認識過程；3從方法論上看，講復雜問題特殊化后就可以解決比較簡單的問題，進而發現解決復雜問題的解法。

（4）推廣的方法

在探求新知識時，人們總是從舊有的知識出發，對舊有知識加以更系統深入的分析和研究，在此基礎上謀求更多的新的知識的發現，稱作"推陳出新"，常用的方法是推廣，即從一個小范疇的事物的研究過度到包含這一小范疇的事物的更廣闊的大范疇的事物的研究。在數學上，對一個定理可以從不同的角度來考慮推廣新的結論。在代數方面，可以對式子中的一些特定的量進行推廣。

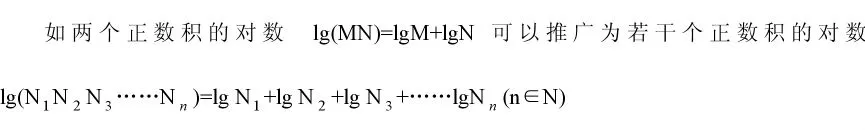
四、逐步逼近的過程

認識是一個過程，是思維對客體的永遠接近。

某些新穎的數學問題，難以找到某個題型為仿解的基礎，但如果可以判斷，該問題的"解"可以按某種方式一步步地逼近之；或者，它的"解"可能存在的區域，通過某一種設計合理的方式，從無限集可結到一個有限集，進而還可以一次次地把"解"的可能存在域縮小、再縮小……，以盡量減少直接檢試的個數、次數。這是我們這里所說的逐步逼近的又一層意思。

1.順推

從已知條件和有關的知識出發，你能推出些什么？再進一步呢？分別考慮各個部分，各個細節，看能否在往前推進一點？

順推，猶如從石堆里抓老鼠時，可以在通過各種信息估計老鼠所藏的地方（結論之所在），把石頭一塊接一塊地搬開（這就更接近目標了！），以達到最求的目的；又如攻城堡時，把外圍的零星據點一個接一個地拔除，以最終攻克城堡。順推時，要注意瞄準結論，即我們將"奔向"的“目標”。

2逆溯

逆溯就是從結論出發，向條件逐步推倒，即不斷提問：通常有哪些途徑，可以算出所要求的某一個量，或推導出所需要的一個結論？在逆溯一步！

逆溯是圍繞著目標的思考。猶如指揮中樞在作戰地圖前集中討論戰斗方案時，總是圍繞著將要被攻克的目標進行多方面、多角度的分析一樣。逆溯時，要時時對照條件。猶如制訂作戰方案時，不能超越本身的條件一樣。

以上借分析例題闡發思想方法，用思維規律啟示引導解題過程，旨在讓更多同行參加探討，讓數學解題更具科學性。

[1]朱勻華主編.中學數學思考方法與解題途徑.中山大學出版社，1984.8.

[2]蘇式冬主編.中學數學研究[M].廣東教育出版社，1990.12.

（作者單位：云浮市中等專業學校）

（編輯 王旸）