響應曲面法優化同向旋轉雙螺桿擠出機最大固體輸送量的研究
袁捷朝,羅 兵,畢 超,王文飛,伊大龍
響應曲面法優化同向旋轉雙螺桿擠出機最大固體輸送量的研究
袁捷朝,羅 兵*,畢 超,王文飛,伊大龍
(北京化工大學機電工程學院,北京100029)
采用響應曲面法對φ34 mm同向旋轉雙螺桿擠出機的最大固體輸送量進行研究。建立了以最大固體輸送量為目標函數的二次式多項數學模型,探討了目標函數的主要影響因素及其交互作用。結果表明,模型所預測的最大固體輸送量和實驗值之間的誤差小于10%,當螺桿轉速為124 r/min、螺紋元件螺旋升角為32°、物料粒徑為2.7 mm時,最大固體輸送量達到534 g/min,這比優化前的最大固體輸送量提高了7.2%。
同向旋轉雙螺桿擠出機;固體輸送;響應曲面法;優化
Abstract:The maximum output of solid convey forφ34 mm co-rotating twin screw extruder was optimized by response surface methodology method.A quadratic multinomial equation model using the maximum output of solid convey as the objective function was built,and the main influencing factors and their corresponding relationships were discussed.It showed that the deviation between predicted values by the model and experimental values was less than 10%.The maximum output of solid convey was obtained as follows,screw speed was 124 r/min,the helix angle of the screw was 32°,and the diameter of the solid particle was 2.7 mm.After optimizing the factors,the maximum output of solid convey was 534 g/min and was increased by 7.2%compared with the value before optimizing.
Key words:co-rotating twin screw extruder;solid convey;response surface methodology;optimization
0 前言
雙螺桿擠出機在聚合物加工中的應用十分廣泛。同向雙螺桿擠出機固體輸送段主要使用計量加料,螺槽一般為非充滿狀態,其輸送機理較為復雜。近年來國內外的學者也對同向雙螺桿的固體輸送現象和機理進行了一定的研究。Carrort等[1]認為嚙合同向旋轉雙螺桿固體輸送有2種機理,即沿螺槽方向的輸送以及在上嚙合區沿軸向的正位移輸送,并認為上嚙合區的正位移輸送量就是全部的正位移輸送量。Potente等[2]將輸送區分成部分填充進料和完全填充壓縮區,建立了力和力矩方程,求解得到最大輸送量。劉廷華等[3]根據可視化實驗觀察有色示蹤粒子的運動,建立了側螺槽非充滿散粒體態的固體輸送模型,以區域型和邊界型相結合的數值計算方法求解了應力場和速度場。張沛和郭強等[4-5]利用可視化實驗研究螺紋元件中的粉料和粒料輸送特性,并建立具有3個子輸送區的固體輸送理論模型。
雖然前人對固體輸送機理和模型進行了大量而有效的研究,但由于固體輸送機理較為復雜,影響固體輸送行為的因子較多,目前建立的模型與實際情況都有一定的差異,有的模型只考慮了單個因子對固體輸送行為的作用,但未考慮因子之間的交互影響。因此,本文擬用響應曲面法來分析同向旋轉雙螺桿固體輸送段最大固體輸送量的影響因子,研究其對目標函數的線性、曲面和交互作用,并在研究基礎之上對影響因子進行優化。
響應面分析法由1組數學和統計學方法組成,可用于確定各因子及其交互作用在加工過程中對非獨立變量的影響,精確地表述因子和響應值之間的關系[6]。采用該統計學方法,能以較少的實驗次數和時間對實驗進行全面的研究。本文所采用響應曲面法中的Box Behnken設計法是以回歸方法作為函數估計的工具,將影響因子和實驗結果之間的關系函數化,定量地分析各因子及彼此之間交互作用對響應值的影響。
1 實驗部分
1.1 主要原料
聚丙烯,粒料,平均粒徑3.8 mm,北京燕山石化公司;
聚對苯二甲酸乙二醇酯,粒料,平均粒徑3.1 mm,美國杜邦公司;
聚酰胺6,粒料,平均粒徑2.4 mm,北京燕山石化公司。
1.2主要設備及儀器
雙螺桿擠出機,LSM30/34,德國Lestritz公司;
臺式干燥箱,DG/200-002,重慶試驗設備廠。
1.3 實驗步驟
主機轉速為90~130 r/min-1,螺紋元件螺旋升角為17°~35°,物料粒徑為2.4~3.8 mm。由于實驗和物料條件所限,實驗中選取了3種粒徑不同的物料,可能對實驗結果產生一定影響。
實驗裝置如圖1所示,實驗前先將物料干燥,對每種物料加料量進行標定。擠出機AB段即為擠出機的固體輸送段,其長度為10D(D為螺桿外徑),可以置換不同螺旋升角的螺紋元件。實驗過程中,按照設定值調節螺桿轉速,進行計量加料,逐漸增大加料量,得到溢流前的加料量即為該種工況下的最大固體輸送量,變換不同升角的螺紋元件、主機轉速和物料粒徑,得到不同工況下的最大固體輸送量并記錄,該實驗均在常溫下進行,機筒不加熱。

圖1 實驗裝置示意圖Fig.1 Schematic diagram for the experimental equipment
2 結果與討論
2.1 因素及水平的選取
響應曲面的實驗設計分為2個步驟,第一步為單因子實驗,其目的為篩選對實驗響應值影響較大的因子,單因子實驗結果表明,主機螺桿轉速、螺紋元件螺旋升角和物料粒徑對最大固體輸送量有較大影響;第二步為響應曲面實驗,其目的為進一步研究影響因子的顯著性和交互作用,本文的響應曲面實驗采用Design-Expert軟件中的Box-Behnken方法,選取主機螺桿轉速、螺紋元件螺旋升角和物料粒徑作為基礎優化因子,以最大固體輸送量為響應值,實驗因數及水平見表1。

表1 Box-Behnken實驗影響因素及水平Tab.1 The factors and their levels of Box-Behnken experiment
2.2響應曲面結果分析
響應曲面實驗方案及實測結果如表2所示。方差分析如表3所示。通過對表2的實驗數據進行多項式回歸分析建立二次響應回歸模型,擬合得到二次方程:

從表3可以看出,實驗所選用的模型擬合度較好。回歸方程的方差分析結果表明,回歸方程的F值達到179.02,說明該模型顯著,回歸方程的決定系數達到99%以上,該模型能夠用于雙螺桿擠出機最大固體輸送量的預測。
式(1)的回歸系數顯著性檢驗表明:因子A、B、C對最大固體輸送量的線性效應皆顯著,因子A2、B2、C2對最大固體輸送量的曲面效應顯著,因子A C對最大固體輸送量的交互效應顯著,因子AB、B C對最大固體輸送量的交互效應不顯著。顯著性檢驗結果見表4。

表2 Box-Behnken實驗設計及實測結果Tab.2 Design and result of Box-Behnken experiment

表3 最大固體輸送量二次多項式模型方差分析Tab.3 Variance analysis for quadratic polynomial model of the maximum output of solid convey

表4 最大固體輸送量回歸方程顯著性檢驗Tab.4 Significance test of regressive coefficient from the regression equation of maximum output of solid convey
圖2為物料粒徑一定(3.1 mm)時,螺桿轉速和螺旋升角對最大固體輸送量交互影響效應,從圖2可以看出,二者的交互作用不顯著。
圖3為螺旋升角一定(26°)時,螺桿轉速和物料粒徑對最大固體輸送量的交互影響效應,從圖3可以看出,當螺桿轉速較低時,粒徑為3.1 mm時固體輸送量達到最大值;當螺桿轉速較高時,粒徑為2.75 mm時固體輸送量達到最大值,這說明螺桿轉速和物料粒徑對最大固體輸送量有著較為明顯的交互作用。

圖2 螺桿轉速和螺旋升角交互影響最大固體輸送量的曲面圖Fig.2 Surface layer of the mutual-affection of screw speed and helix angle of screw on the maximum output of solid convey
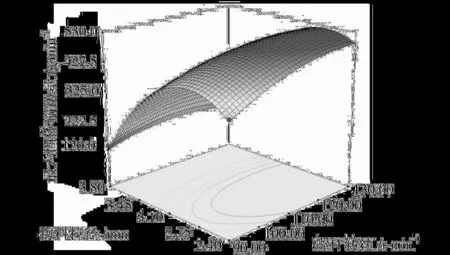
圖3 螺桿轉速和物料粒徑交互影響最大固體輸送量的曲面圖Fig.3 Surface layer of the mutual-affection of screw speed and diameter of solid particle on the maximum output of solid convey
圖4 為螺桿轉速一定(110 r/min)時,螺旋升角和物料粒徑對最大固體輸送量的交互影響效應。從圖4可以看出,二者的交互作用不顯著。
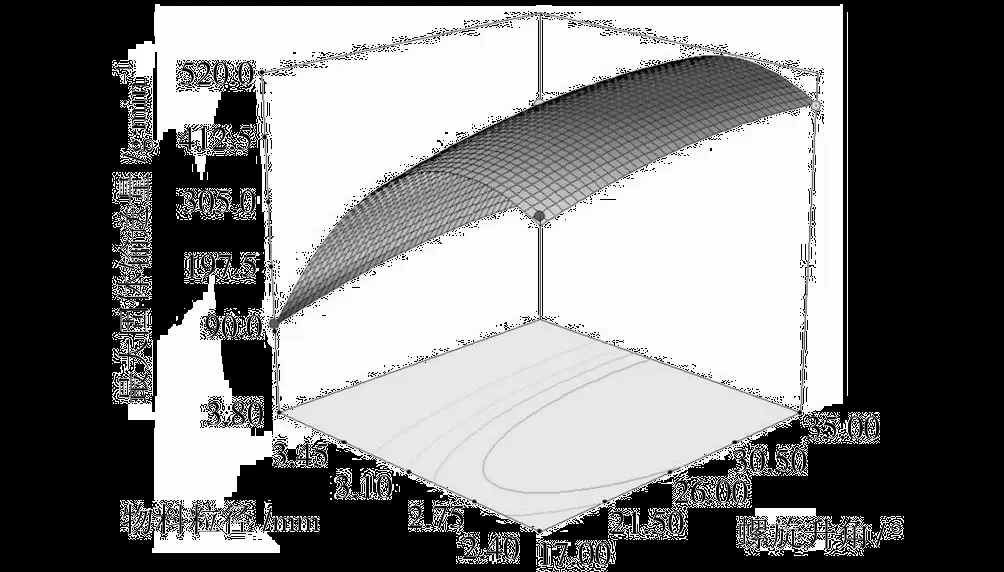
圖4 螺旋升角和物料粒徑交互影響最大固體輸送量的曲面圖Fig.4 Surface layer of the mutual-affection of helix angle and diameter of solid particle on the maximum output of solid convey
2.3方程的驗證和應用
為驗證回歸方程(1)的準確性,選取6組前文實驗設計中沒有用到的工藝條件進行固體輸送實驗,同時使用回歸方程對該6組工藝條件下的最大固體輸送量進行預測,將得到的實驗結果和回歸方程的預測值進行分析和對比,得到的最大固體輸送量的預測值與實測值如表5所示。從表5可以看出,理論值和實測值的誤差均在10%之內,說明響應曲面法所建立的模型與實驗所得到的數據比較吻合,其誤差可能來自于實驗條件和測量精度的限制。

表5 最大固體輸送量的實測值及預測值Tab.5 Experimental values and prediction values of the maximum output of solid convey
對方程(1)的各參數進行優化分析,可以得到3個因子的最佳水平為螺桿轉速124 r/min、螺紋元件螺旋升角32°、物料粒徑2.7 mm,此時最大固體輸送量為534 g/min,這一優化值比表2中固體輸送量的最大值提高了7.2%。
3 結論
(1)通過響應曲面法建立了影響主機最大固體輸送量的二次多項數學模型,探討了各因子之間的交互作用。通過對最大固體輸送量二次多項式數學模型進行求解,將模型得到的理論值與實測值進行對比,證明該模型與實測值之間的誤差在10%以內,能夠用于最大固體輸送量的預測;
(2)由響應曲面實驗分析可知,提高最大固體輸送量的最佳水平為螺桿轉速124 r/min、螺紋元件螺旋升角32°、物料粒徑2.7 mm,此時的最大固體輸送量為534 g/min,這一優化值比優化前最大固體輸送量提高了7.2%。
[1] Carrot C,Guillet J,MayJ F.Modeling of the Conveying of Solid Polymer in the Feeding Zone of Intermeshing Corotating Twin Screw Extruders[J].Polymer Engineering&Science,1993,33(11):700-708.
[2] Potente H,Melisch U.Theoretical and Experimental Investigations of the Melting of the Pellets in Co-rotating Twin Screw Extruders[J].Int Polym Process,1996,11(2):101-108.
[3] 劉廷華,朱復華.嚙合型同向旋轉雙螺桿擠塑螺槽非充滿的固體輸送的理論研究(Ⅰ)理論模型[J].中國塑料,1996,10(9):81-85.
[4] 張 沛,耿孝正,朱林杰.同向嚙合雙螺桿固體輸送特性的可視化研究——螺紋元件的粉料輸送[J].中國塑料,1999,13(5):90-95.
[5] 郭 強,耿孝正,張 沛.同向嚙合雙螺桿固體輸送可視化研究——螺紋元件的粒料輸送[J].中國塑料,1998,12(5):85-93.
[6] Annadurai G,Sheeja R Y.Use of Box Behnken Design of Experiments for the Adsorption of Verofix Red Using Bionpoly[J].Bioproc Eng,1998,18:463-466.
Optimization of Maximum Output of Solid Convey for Co-rotating Twin Screw Extruders by Response Surface Methodology
YUAN Jiechao,LUO Bing*,BI Chao,WAN G Wenfei,YI Dalong
(School of Mechanical Engineering,Beijing University of Chemical Technology,Beijing 100029,China)
TQ320.66+3
B
1001-9278(2011)01-0102-04
2010-08-16
中央高校基本科研業務費項目(ZZ0913)
*聯系人,luobing@mail.buct.edu.cn

