AS級Internet拓撲層次性分析與建模

郭虹，楊白薇，蘭巨龍，劉洛琨

（1. 國家數字交換系統工程技術研究中心，河南 鄭州 450002;

2. 信息工程大學 信息工程學院 通信工程系，河南 鄭州 450002）

1 引言

近些年來，Internet的商業化行為促使互聯網快速成長，現今 Internet已滲透到社會生活的方方面面。但是，人們對支撐各種網絡應用的互聯網拓撲的內在結構特征和演化規律的理解卻遠未成熟。當前全球范圍內正掀起重新規劃和設計新一代互聯網的熱潮，下一代互聯網的研究和設計將秉承繼承和發展的思路。需要對當前互聯網的基礎設施和行為進行充分、深入地認識。

基于拓撲測量，對互聯網進行拓撲特征分析，從中提取出標識網絡內在結構的主要特征，是有效利用和進一步指導網絡建設的重要前提；利用拓撲分析結論模擬構建出網絡拓撲，能為許多不便于在實體網絡上開展的實驗和協議開發、研究提供準確的網絡仿真環境；而將模型生成的拓撲特征與實際網絡進行對比、評估，能進一步加深人們對實際互聯網拓撲的認識和理解[1,2]。

互聯網拓撲按不同粒度劃分為路由器級(RL,router-level)和自治域 (AS, autonomous system)級。與RL級相比，AS級位于更“高”一層，其特征與變化對互聯網的影響更為巨大，相關研究對下一代網絡的發展意義更為重大；而且AS 級規模相對RL級規模小得多，能夠進行更深層次、更復雜的計算分析，以探究更為隱秘的客觀特性和規律[2]。

自 20世紀末復雜網絡研究興起后，許多拓撲宏特征被定義以刻畫拓撲結構的內在特性，包括節點度分布、平均路徑長度、聚集系數、同配系數和富人俱樂部系數等。為了向互聯網研究人員提供更準確的網絡拓撲模型，拓撲建模研究者先后提出了大量的拓撲模型或生成算法，如隨機網絡模型、層次模型、小世界模型、冪律模型、局域世界模型等。其中，Waxman、Transit-Stub[3]、WS、BA、LW[4]、PFP[5,6]等模型比較著名。但是，早期的互聯網拓撲建模研究受限于拓撲數據的獲取，對拓撲的內在機理認識不足，且大多數模型側重于對度優先偏好連接和冪律度分布的刻畫，對實際互聯網的其他拓撲特征刻畫還存在一定的差距[7]。

“層次性”是互聯網中普遍存在的基本特性之一。互聯網的規劃建設及商業模式特點使其呈現出明顯的層次結構。了解、量化網絡的層次性有助于人們更深入地認識互聯網的內在拓撲特性，對于研究互聯網的演化機制非常重要。早期基于對“層次性”的直觀理解，將網絡劃分為 Stub域或 Transit域，提出了具有嚴格層次結構的互聯網靜態拓撲模型Transit-Stub[3]。文獻[8]在研究了復雜網絡中的層次組織后提出了層次模塊性，并給出一種網絡層次性的數學刻畫——簇度相關性。為研究網絡核心結構，文獻[9]提出了核數以及k-core分解以量化節點的中心程度。文獻[7,10]初步探討了節點度與核數之間的關系，建立了靜態的層次模型。

鑒于目前對AS級拓撲層次性分析、建模不足，本文基于對互聯網實測數據的層次性分析，提出了一種對真實互聯網AS級拓撲層次特征符合程度更逼近的建模方法，并通過計算機建模仿真分析說明其合理性及有效性。

2 AS級拓撲的層次性質

AS級拓撲可抽象為點和邊組成的無向簡單圖，節點代表自治域(AS)，邊則代表AS之間的BGP連接。AS級拓撲具有隨機性、小世界現象、冪律性、聚集性、層次性和富人俱樂部現象等性質[1]。

2.1 度的高可變性

1999年，Faloutsos 3兄弟在對互聯網數據分析時發現其拓撲的節點度分布表現出形如P(k)∝k-λ的冪律，在雙對數坐標中近似為一條斜率為-λ的直線。冪律分布的發現顛覆了稱霸多年的隨機網絡模型，揭示出互聯網拓撲的一個重要性質——度的高可變性：即拓撲中節點度值的范圍很大，大部分節點的連接度較小，少部分節點的連接度很大。度的高可變性揭示出在AS級拓撲中不同節點扮演不同的角色：少數的高度值節點成為Hub節點，負責全網的連通性，網絡中存在層次性。

2.2 層次性

冪律是基于節點度對拓撲的局部描述，層次性則是對其的宏觀描述。1997年，Paxson基于拓撲實測數據，提出基于節點度值將AS級互聯網劃分為4個層次，初步揭示了兩者之間的內在聯系。但是，度僅代表了最少的局部信息，基于節點度的層次性劃分方法存在一定的偏差和主觀性[11]。

2.3 簇度相關性

文獻[8]在對復雜網絡的實證研究中發現，受地理因素限制的網絡缺乏層次性，例如美國西部電力網和路由器層網絡；而AS級Internet中節點的地理位置因素不確定也不重要，具有明顯的層次性，并給出了網絡中層次性的定量刻畫——簇度相關性，發現AS級拓撲的簇度關系近似為

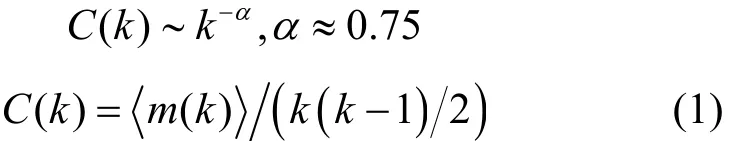
其中，＜m(k)＞表示度為k的所有節點的鄰居之間平均存在的邊數，C(k)表示度為k的節點的平均簇系數[12]。

2.4 核數

一個圖的k-核是指反復移除圖中所有節點度小于等于k的節點及其連接的邊，直到所有剩余節點的度都大于k所余下的子圖[13]。

定義1 節點的核數：如果一個節點屬于k-核，而不屬于(k+1)-核，則該節點核數為k。節點的核數越大，越意味著該節點位于拓撲圖的中心。

定義 2 圖的核數：圖中節點核數的最大值即為圖的核數。

由定義1和定義2知，節點/圖的核數能夠標識出節點/子圖在拓撲圖中的深度，核數較節點度值具有更客觀的層次性刻畫能力。

3 AS級拓撲的層次性分析

本節基于AS級Internet拓撲的實測數據，對其進行層次性分析。

3.1 數據來源

AS級拓撲數據獲取主要有2種方式：1) 基于BGP路由表和更新消息推測的被動測量方式，如量方式，將測量出的 IP路徑映射為 AS路徑，如但獲取的僅是控制層面的拓撲，且由于ISP通常將BGP路由信息視作商業機密，通過推測BGP路由信息將無法獲得ISP未對外公開的私有連接。主動測量相對難實現，但展現的是數據層面的拓撲。為客觀分析AS級拓撲的層次性，本文采集、綜合了取出2003年12月到2006年12月共7個真實的一個真實的AS級拓撲圖。

3.2 基本拓撲特性

本節對上述數據集逐一進行拓撲特性分析，如表1所示。其中，N和E分別是拓撲圖中總的節點數和邊數；是平均節點度；是平均最短距離；＜C＞

由表1可知，隨著時間的演化，真實互聯網呈現指數的加速增長；網絡同時具有小的平均最短距離和大的平均聚集系數，具有小世界效應；網絡的同配系數 r≈-0.23，意味著低度值節點的鄰居中大部分是高度值節點，低度節點傾向于和高度節點連接；k≤3的節點占全網的絕大多數，網絡中不穩定的部分主要是度值為1的葉子節點。表1的分析結果與文獻[20]的結論一致。

3.3 層次性分析

1) 拓撲圖的核數與最高核

拓撲圖的核數與最高核對于層次性分析具有重要意義。對上述數據集的核數與最高核情況進行絡節點數，En為最高核內的連接數，Ep(為與最高核相關連接的比例。由表2可知，隨著時間推移，Internet的網絡規模不斷增長，AS級拓撲圖的核數2004年以后逐漸趨于28；最高核所含節點數占全體節點數的比例在0.182%～0.511%之間；最高核內連接數占全網總連接數的比例在 1.17%～3.05%之間；外部節點與最高核的相關連接占了全網總連接的很大一部分，在44.41%～54.95%之間。充分說明真實 AS級互聯網中網絡的核心很少突然出現或消失，近年來一直趨于穩定；最高核內連接稠密，影響力滲透到全網，決定并影響著網絡的整體性能，非常重要。

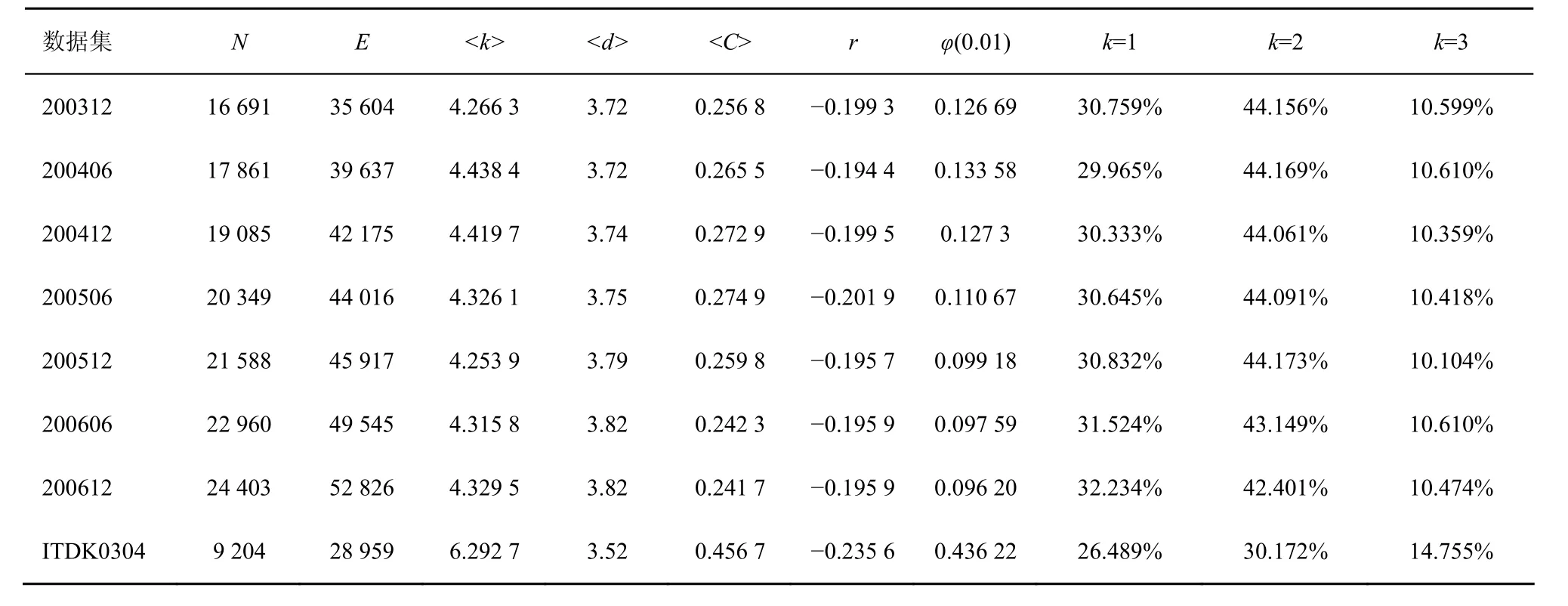
表1 AS級Internet的基本拓撲特性

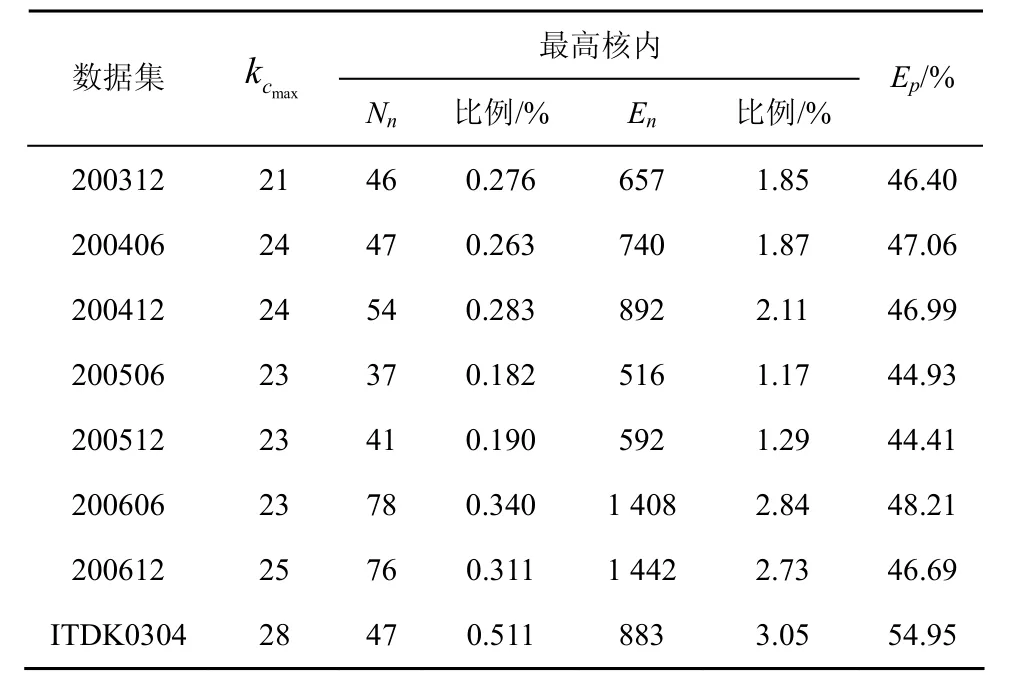
表2 AS級Internet的核數與最高核分析

2) 節點的核數-度分布

節點核數標識節點在拓撲圖中的深度，拓撲圖中各節點的核數與其度值之間存在著一定的關系，了解拓撲圖中節點的核數-度分布是認識AS級拓撲層次性的一個重要度量。圖1(a)給出ITDK0304數據集的節點核數-度分布，為雙對數坐標。

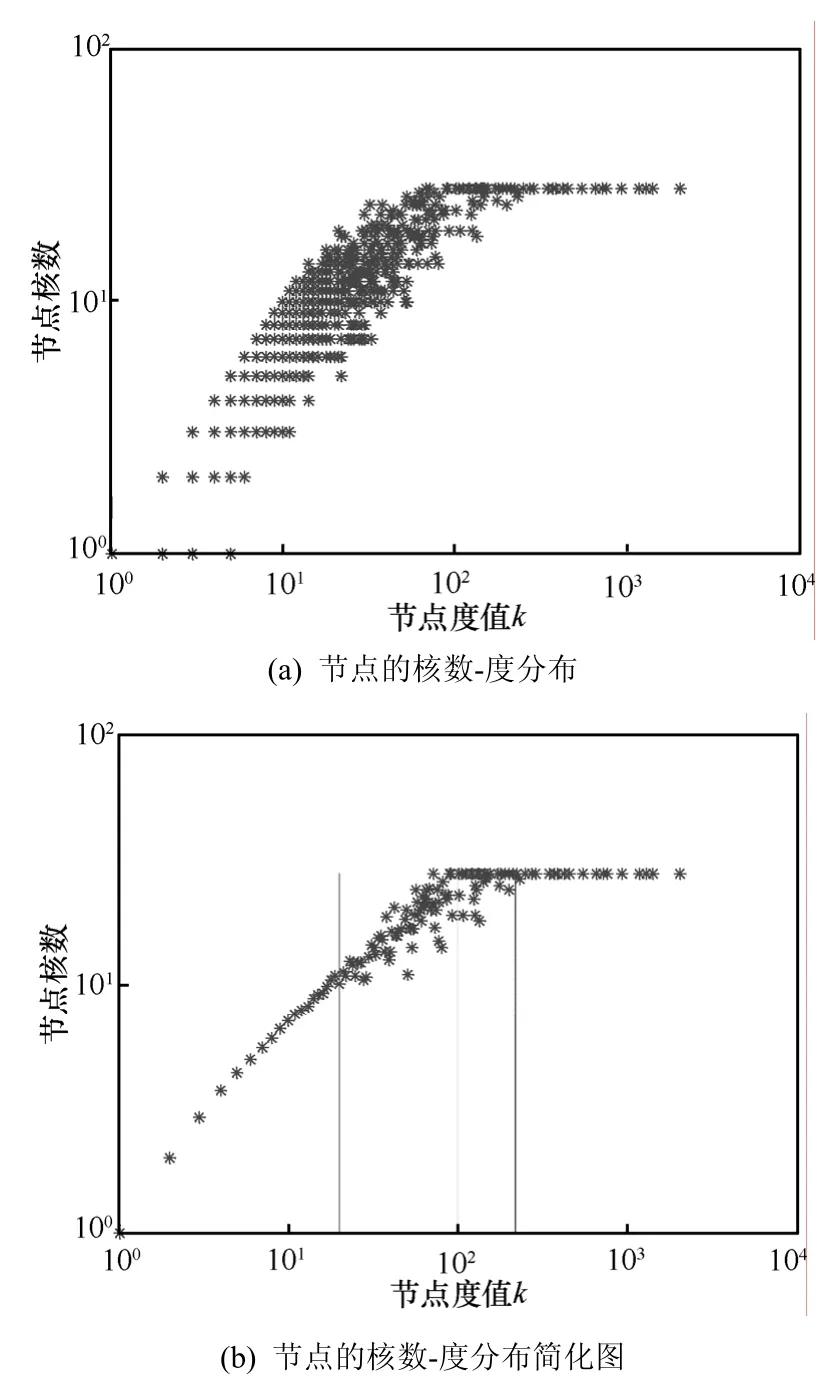
圖1 ITDK0304拓撲圖的節點核數-度分布

由圖1(a)可以看出真實AS級拓撲中各核數內節點的度值較為分散，度值越大的節點具有高核數的可能性越大，但是，即便一個節點的度數很高，它的核數也可能很小。為使兩者之間的關系明晰，對相同度值，取全體節點核數的平均值，得到簡化圖，如圖 1(b)所示。由簡化圖可以看出，AS級拓撲中低度值節點(k＜20)的核數與度值呈正相關；高度值節點(k＞120)主要集中于高核區域內，且隨著度值的增加，節點核數不再增加；但部分高度值節點(20＜k<120)的核數散落于其他層。

3) 拓撲圖的k-core分解

k-core分解是一種非常有效的提取網絡中心部分的方法。為進一步研究AS級拓撲圖中各核的細節，對上述數據集逐一進行k-core分解，記錄各核內節點的數目 N(kc)、占全網節點數的比例 Np、平均度值＜k＞、平均連接數＜cn＞、各核所擁有的連接占全網總連接的比例E1、各核內部連接占該核所擁有連接的比例E2、各核與最高核的連接占該核所擁有連接的比例E3。

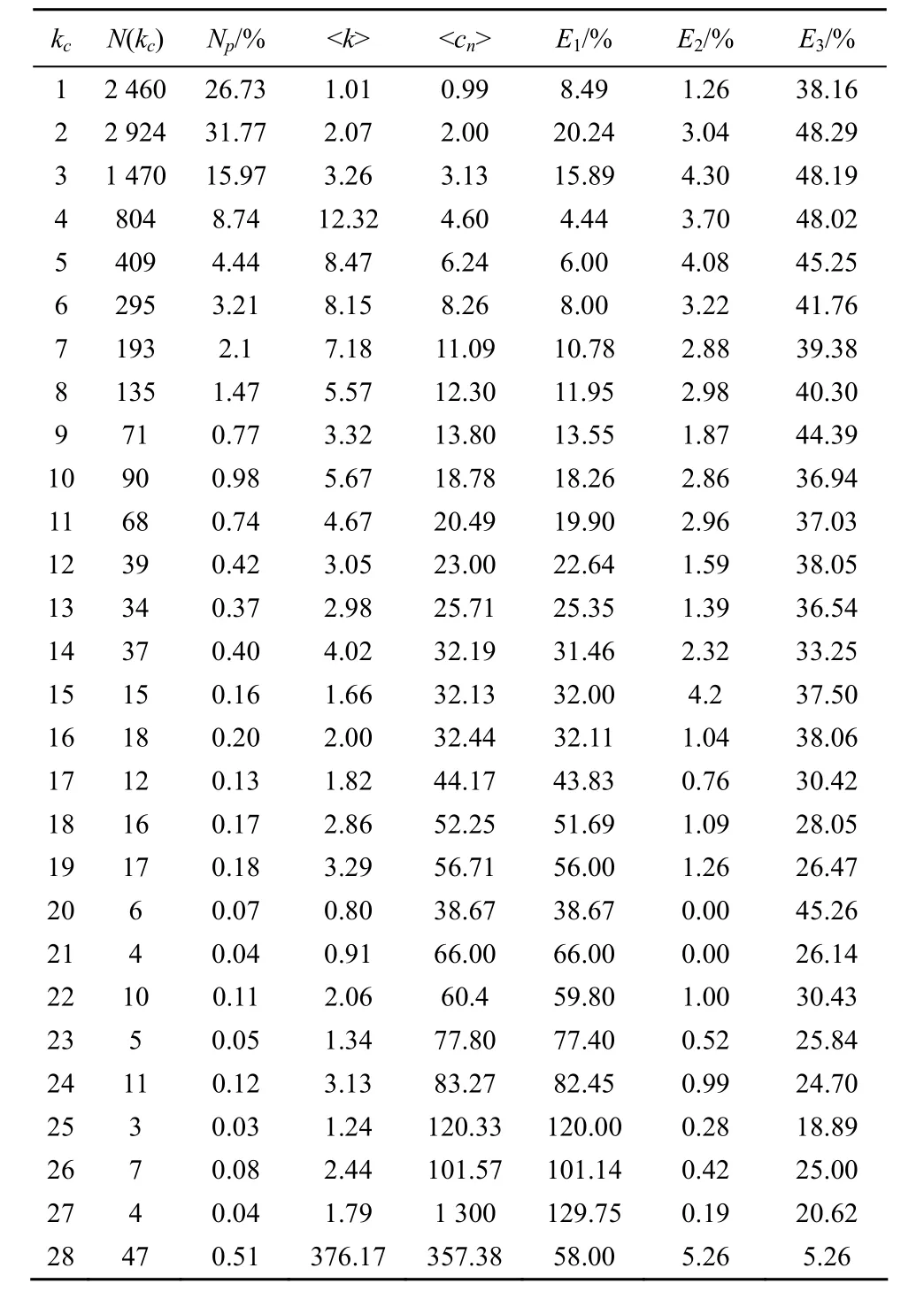
表3 ITDK0304數據集的k-core分解

由表3的k-core分解結果，可知以下幾點。

① 隨著 kc的增大，真實的 AS級拓撲圖中各核子圖的尺寸雖然有一些波動，但相較全網規模的增長各核節點比例幾乎是穩定的；各核所擁有的連接占全網總連接的比例 E1也基本穩定，只在 kc=1,2,3處波動大一點，說明網絡中不穩定的部分主要是低核數（也是低度值）節點。

② 核數較低(kc=1,2,3)的節點占總節點數的大部分(74.47%)，其余核數(kc＞3)節點數較少。

③ 最高核包含了大量的“度”，意味著最高核雖然只包含著少數節點，但都為高度值節點，0.5%的最高度值節點都在最高核內。

④ 與最高核有關的連接占據網絡連接中相當大的一部分(58%)；最高核內部的連接只占該核所擁有連接的5.26%，其余大部都分散在與其他各核之間的連接上。說明最高核的影響力巨大，滲透到網絡的各個核數內。

⑤ 與低核數節點相關的連接也占據了網絡連接中的相當一部分(44.62%)，而這些核內部的連接只占核所擁有連接的的很小一部分(1.26%～4.3%)，其余部分均是與最高核的連接。

說明最高核影響力巨大，滲透到網絡的各個核數內，對其的刻畫將決定整個層次模型的成敗。

4) 拓撲圖的簇度分布

圖2給出ITDK0304的簇度分布，表明在真實的互聯網AS級拓撲圖中C(k)與k之間確實存在著高度的負相關性，并隨著k的增加而遞減，遞減的斜率大致在-0.75左右。但目前很多互聯網拓撲模型并不能很好地再現這一負相關性。

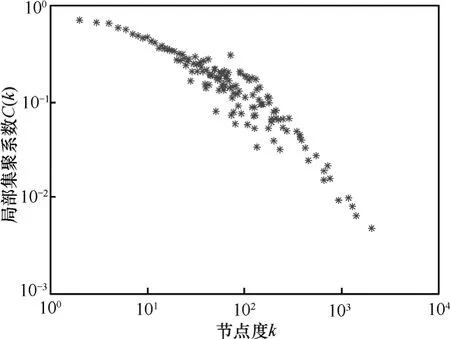
圖2 ITDK0304拓撲圖的簇度分布

4 AS級拓撲層次建模

按據層次性分析結論，建立基于核數劃分的AS級互聯網拓撲層次動態演化模型 IAT-HDEM(Internet AS-level topology hierarchical dynamic evolution model)。

4.1 層次模型的關鍵

層次模型的關鍵在網絡核心刻畫與層次劃分。

1) 網絡核心刻畫

網絡核心即網絡的最高核，盡管最高核內節點數很少，但最高核的影響滲透到網絡的各個層次；且最高核隨互聯網演化已逐漸趨于穩定。對網絡核心的刻畫決定著層次模型的成敗。如何刻畫網絡核心呢？按據上述數據集的 k-core分解統計結果，IAT-HDEM 模型的最高核數設為maxck=28；最高核內的節點數為 N28=N×0.294 5%，連接平均數為E28=E×2.113 8%。

鑒于最高核內都為高度值節點，由網絡演化視角看，隨著網絡演化，不斷進入網絡的新節點按高概率與網絡的核心節點連接。所以，在基于度擇優偏好連接概率的動態網絡演化模型中，初始網絡內節點成長為高度值節點的概率很大，將網絡核心設為初始網絡。

2) 層次劃分

節點的核數與其地位、規模正相關；節點核數較度值具有更客觀的層次性刻畫能力。表3表明：低核數節點(kc≤3)占據了網絡中絕大部分節點數(74.47%)和連接數(44.62%)；最高核雖然節點比例很少(0.51%)，但與最高核相關的連接卻占了全網連接的一半強(58%)，將最高核單獨刻畫；4～27，各核節點所占比例極低，且隨著核數kc增加，影響力相當，將中間核層合并處理。

層次劃分的設想如下：按照核數高低將網絡內所有節點共劃分為6個層次：Ω1（核數kc=1的節點集），Ω2（核數kc=2的節點集），Ω3（核數kc=3的節點集），Ω4（核數kc=4,5的節點集），Ω5（對應核數kc=6,7,…,maxck-1的節點集），Ω6（對應核數maxck的節點集，為最高核集Ωmax）。

在確定6個層次后，各層次內部的具體細節又如何？以ITDK0304數據集為例，對數據集進行層次分析，如表4所示。由表4可得到IAT-HDEM模型的思想：新節點進入網絡按層次選擇概率 H，選擇相應的層次加入；再按各層間連接概率p選擇目標節點層次；按偏好擇優概率從目標層次中選擇相應的宿主節點加邊連接，實現網絡的動態演化增長。

4.2 基于核數劃分的AS級層次動態演化模型

為建立IAT-HDEM模型，并獲得具體的模型參數，對上述數據集分別進行層次分析，并對相應參數進行算術平均，得到層次建模參數，如表5所示。由表5知，節點加入各層次的概率不同，差別很大；網絡中各層內、層間節點間有相互連接，連接概率不盡相同；各層與網絡核心層的連接相對于與其他層次的連接較多。

1) 模型算法

IAT-HDEM模型算法描述如下。

模型輸入：N，E（期望的網絡規模）。

模型輸出：網絡拓撲的鄰接矩陣A。

模型初始化：建立6個層次集合Ωi，并按Hi確定各集合的最終大小：

網絡演化過程如下。

Step1 產生初始網絡。

m0=N×0.295%，e0=E×2.114%，初始網絡節點間隨機連接，并記錄到A中，形成Ω6=Ωmax。因e0相較 m0而言稠密得多，能確保初始網絡每個節點的度至少為1。

Step2 網絡增長。

① 在每一個時間步增加一個新節點vn。

② 按概率Hi，i=1,2,…,6，選擇新節點vn加入的層次i。當且僅當|Ωi|＜Ni時，新節點vn加入i層，vn∈Ωi；否則回到②。

例如，vn按概率選擇第6層，因為初始網絡已構建完成|Ω6|=N6，所以返回②重新選擇vn加入的層次；由于新節點加入第6層的概率很小(0.263%)，此事件基本不可能發生。但考慮到在網絡逐漸演化過程中，可能出現某一層次先加入完畢的情形，故做此處理。

③ 當 1≤i≤5時，為新節點增添 m條連接。從 vn節點出發，引出 m條邊與宿主節點vhj(j=1,2,…,m)相連。對某個宿主節點 vhj的選擇方法為：按概率pij選擇宿主節點 vhj歸屬的目標層次j，vhj∈Ωj；如果j層次的|Ωj|≤3，則視目標層次節點集合為空，即刻為Ωj增加一個新節點vn'= vhj∈Ωj，連接vn與vn'，轉入④。否則，從Ωj中按非線性擇優出宿主節點 vhj，連接vn與 vhj。對vn節點重復此操作m次，完成新加入節點vn與不同層次不同節點間的m條連接。更新當前網絡內的節點數。

④ 當③中目標層次的節點集合視為空時，為Ωj增加了一個新節點vn'∈Ωj，并連接了vn與vn'。為使對新節點的操作一致，還需要對vn'增加m-1條邊。

重復上述過程，直至網絡增長到期望規模N。

宿主節點的選擇思想為：先選擇宿主節點的層次，再從目標集合中按非線性擇優概率選擇宿主節點。為了突出和說明基于核數劃分層次建模的有效性和合理性，IAT-HDEM模型簡化了網絡演化過程中存在的節點和邊的消亡的模擬。

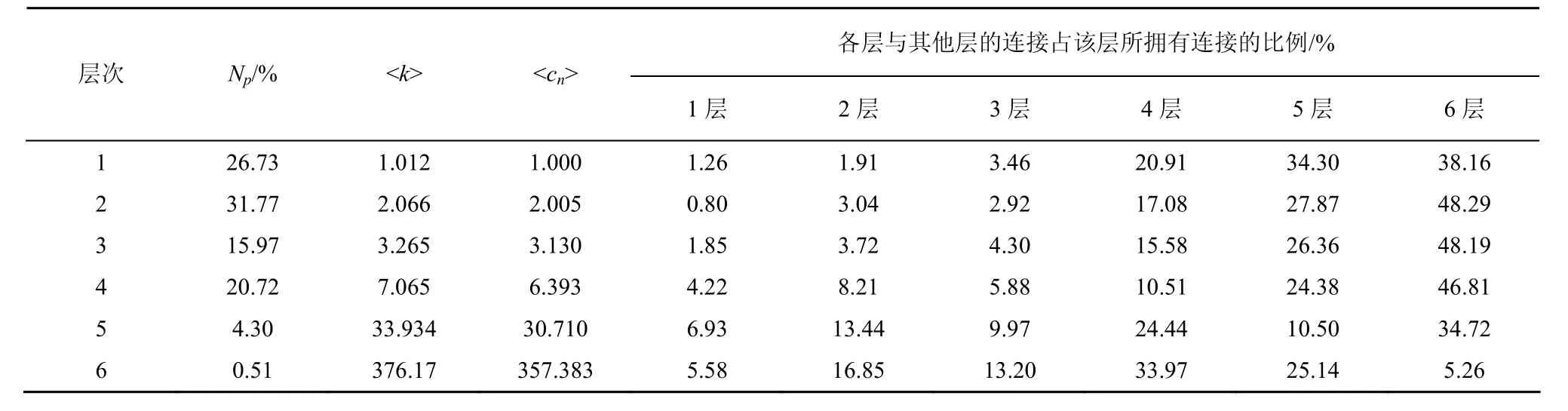
表4 ITDK0304數據集的層次分析

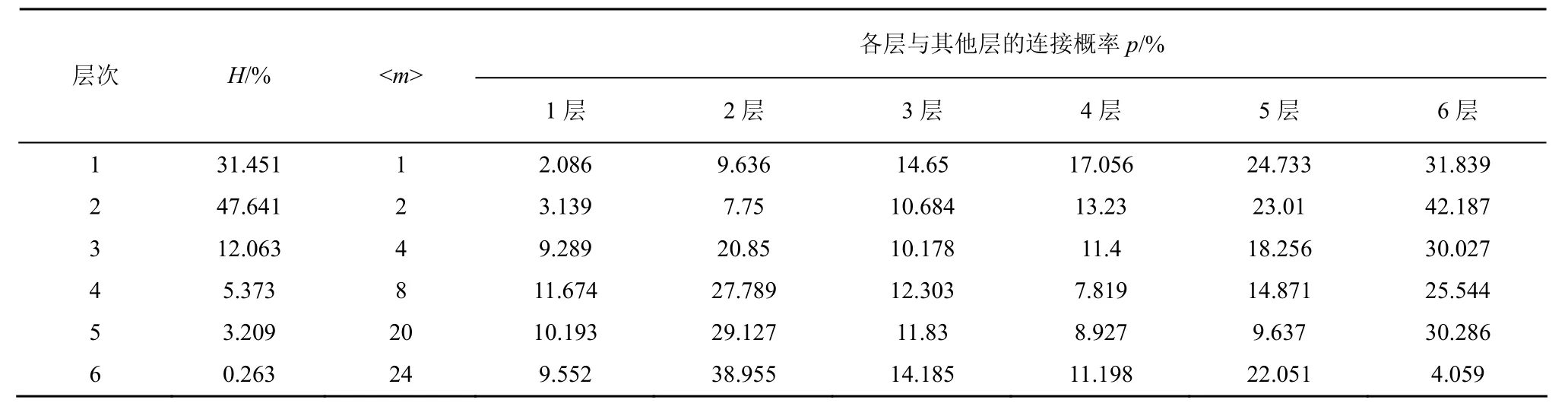
表5 IAT-HDEM模型層次建模參數

2) m的取值與概率

在IAT-HDEM模型中，對新加入各層的節點，為其分配的連接數為m。如果m的取值為固定值，則將導致各層次節點度值過于平均，違背了圖1(a)所反映出的節點核數-度分布的散落性。為避免各層次節點度值過于平均，m的取值應與節點歸屬的層次有關且為變值。即使不同時間步內加入同一層次的不同新節點，其m連接數也應按概率有所不同。

以ITDK0304數據集為例。在第1層，核數kc=1，這層中99.11%的節點度都為1，但是該層也含有少量的度大于1的節點（0.77%的節點度為2，剩余節點度為3或其他）。這意味著，進入第1層的節點其連接數有可能為2或3，但還是以大概率可能為1。按次類推，能分析、計算出各層節點的度分布，進而得出進入各層的節點應以怎樣的概率擁有怎樣的連接數。據此處理，不僅能確保各層節點的平均連接數能與期望值接近，還能避免各層各節點連接數過于同一的情形。

具體IAT-HDEM模型中m的參數按據來自對上述數據集的統計平均。例如，第1層m的取值為1、2、3，對應概率分別為98.30%、1.60%、0.10%；第 2層 m的取值為 2、3、4、5、6、7，對應概率分別為 90.80%、5.60%、1.60%、0.70%、0.70%、0.60%；第3層m的取值為3～15；第4層m的取值為4～29；第5層m的取值為6～60。每一層m的取值范圍，盡可能取到剩余節點所占概率和小于1%。

3) 擇優連接概率

現有的大多拓撲模型，都以優先連接理論為基礎，不同的是各模型的優先連接概率的計算公式。IAT-HDEM模型中在選定目標層次后，采用優先連接方法選擇宿主節點，擇優連接概率[7]為

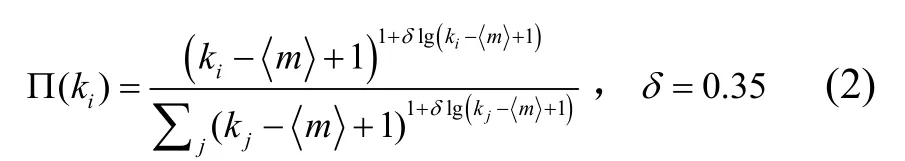
現有的多種優先連接概率公式多以節點度值為計算基數，與之相比略有不同的是，式(2)的基數選取為節點度值與節點歸屬層次的＜m＞（各層的平均連接數）之差。這是因為，在層內優先連接開始時，各層內節點的度值相差不大，基本接近＜m＞，這使得一般的擇優概率難以發揮作用，故要去除各層相應的＜m＞值后再進行擇優。為確保選擇概率不為0，選擇二者之差+1作為計算基數。

4.3 算法復雜度分析

IAT-HDEM模型算法主要分為3步：新節點按層次選擇概率選擇相應的層次加入；再按各層間連接概率選擇目標層次和在目標層次內按偏好擇優概率選擇相應的宿主節點；新節點與宿主節點間連邊，實現網絡的動態演化增長。所以其算法時間復雜度和空間復雜度均與網絡規模相關。由于引入了一些概率模型，算法的復雜度分析較為復雜，但仍可以粗略地進行估算。

時間復雜度介于O(N)和O(N2)之間。該算法需要輸出拓撲的鄰接矩陣A；在算法執行過程中，需要存儲相應的層次集合以及各節點對應的度和連接數等信息。所以，其空間復雜度約為 O(N2+N+2N)= O(N2+3N)。

可見，隨著網絡不斷演化，每個時間步內新加入節點的處理耗時不斷增加；當網絡規模很大時，IAT-HDEM算法輸出整體耗時在指數增長，與計算機仿真實驗的結果一致。

5 計算機建模仿真分析

本文在MATLAB中實現了IAT-HDEM模型，將建模結果與實際網絡進行比較以評價建模方法的優劣。

5.1 IAT-HDEM模型的宏特征

由于節點選擇層次和宿主節點連接按概率發生，每次仿真得到的網絡拓撲有所不同，本文采取多次實驗取平均的方法來統計 IAT-HDEM 模型拓撲的宏特征。文中仿真結果均為 10次獨立實驗取平均，如表6所示。

由表6可以看出，IAT-HDEM模型在相同的參數下，在平均節點度、平均最短距離、平均集聚系數、網絡的同配系數、Rich-club系數、圖的核數、度為1，2，3的節點在網絡中所占的比重方面與真實的AS級拓撲的宏特征接近。

表6 真實AS級拓撲圖與IAT-HDEM模型的宏特征比較

5.2 IAT-HDEM模型的冪律特性

冪律特性是衡量拓撲模型性能的重要指標之一，圖3為IAT-HDEM模型的節點度分布。

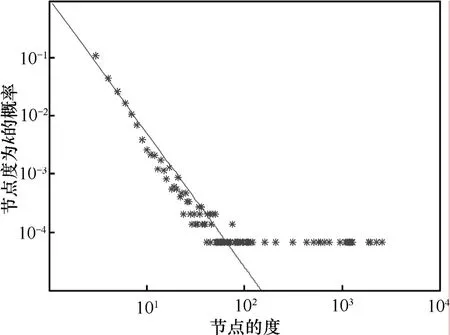
圖3 I IAT-HDEM模型的節點度分布（N=5 000）

由圖3可見，IAT-HDEM模型的節點度分布也呈冪律，且冪律指數并不隨網絡規模的增長而變化，圖中直線為斜率-2.3的冪律曲線，IAT-HDEM模型在冪指數上擬合得也很好。這說明基于核數劃分的層次動態演化模型在冪律特性方面也有突出表現，也從另一個側面說明，增長與優先連接并非唯一決定網絡拓撲冪律特性的重要因素，層次性也影響著網絡的冪律特性。

5.3 IAT-HDEM模型的層次特性

圖4給出IAT-HDEM模型的節點的核數-度分布，與圖1對比，IAT-HDEM模型呈現出類似的節點核數-度分布趨勢，略有不同的是，IAT-HDEM模型中高度值節點的核數整體偏小一些，這是由于實驗網絡規模所致。

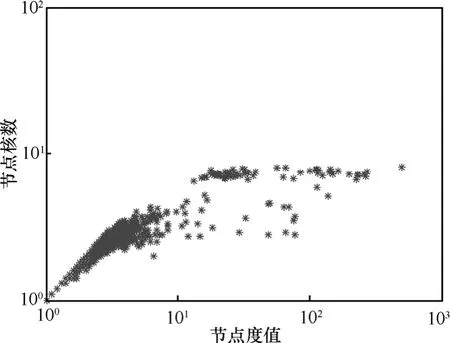
圖4 IAT-HDEM模型拓撲圖的節點核數-度分布（N=5 000）

圖5 給出IAT-HDEM模型的簇-度分布，與圖2對比，IAT-HDEM模型呈現出明顯的負的簇度相關性且斜率大致在-0.7左右，與文獻[8]結論一致。這說明即使基于核數劃分的 IAT-HDEM 模型也能呈現出傳統意義上的層次性。圖5進一步說明簇度的負相關性是增長網絡模型內在固有的特性之一[21]。

圖5 IAT-HDEM模型拓撲圖的簇度分布（N=5 000）

計算機建模仿真分析表明，IAT-HDEM 模型能較好地模擬真實互聯網AS級拓撲的宏特征、冪律特性和層次特性，是一種模擬互聯網AS級拓撲層次的動態演化模型。該模型具有如下優點：1) 以實測量數據為背景，優化模型參數，對真實拓撲模擬較好；2) 模型既能夠反映出AS級拓撲的層次性特性，同時又保留了其他多種特征；3) 該模型的提出，能夠為Internet拓撲建模構建一個較為合理的框架，例如可以基于層次劃分對AS間的商業關系進行建模。

6 結束語

本文基于對AS級Internet拓撲實測數據的層次性分析，提出了一種基于核數劃分的AS級互聯網層次動態演化模型(IAT-HDEM)。該模型以節點核數作為層次劃分按據，是按照拓撲圖自身內在的層次性進行劃分，角度重更為合理、細致。計算機建模仿真分析表明，該模型能較好地模擬出真實互聯網AS級拓撲的宏特征、冪律特性和層次特性。模型的提出，對進一步分析層次性質對網絡拓撲的重要意義提出了思路；此外，該模型可以作為 AS級Internet網絡拓撲建模的一個基本框架，在此框架基礎上，可以繼續刻畫其他拓撲特性，例如AS級的商業關系；或者添加AS節點和邊的生、滅描述等，這將是下一步的研究工作。基于測量建立拓撲模型，這正是互聯網拓撲建模研究現階段被忽略的，本論文的工作做了良好嘗試，而模型參數的可測性會對模型價值產生重大影響，對于探究網絡的演化機理意義重大。

[1] 楊家海, 吳建平, 安常青. 互聯網絡測量理論與應用[M]. 北京: 人民郵電出版社, 2009.299-324.YANG J H, WU J P, AN C Q. Internet Measurement Theory and Applications[M]. Beijing: Posts & Telecom Press, 2009.299-324.

[2] 周苗,楊家海,劉洪波等. Internet 網絡拓撲建模[J].軟件學報,2009,20(1):109-123.ZHOU M, YANG J H, LIU H B, et al. Modeling the complex Internet topology[J]. Journal of Software, 2009,20(1):109-123.

[3] ZEGURA E W, CALVERT K L, DONAHOO M L. A quantitative comparison of graph-based models for Internet topology[J].IEEE/ACM Transactions on Networking, 1997, 5(6): 770-783.

[4] LI X, CHEN G A. Local-world evolving network model[J]. Phys A,2003, 328: 274-286.

[5] ZHOU S, MONDRAGón R J. Accurately modeling the Internet topology[J]. Physical Review E, 2004, 70(6):8-15.

[6] ZHOU S. Characterising and modelling the Internet topology the rich-club phenomenon and the PFP model[J]. BT Technology Journal,2006, 24(3):108-115

[7] 張昕, 趙海, 王莉菲等. AS級Internet拓撲分析[J]. 通信學報, 2008,29(7): 50-61.ZHANG X, ZHAO H, WANG L F, et al. Analysis on the Internet AS-level topology[J]. Journal on Communications, 2008, 29(7): 50-61.

[8] RAVASZ E, BARABáSI A L. Hierarchical organization in complex networks[J]. Physical Review E, 2003, 67(2):12-20.

[9] GAERTLER M, PATRIGNANI M. Dynamic analysis of the autonomous system graph[A]. Proceedings of IPS 2004[C]. Budapest, Hungary,2004.

[10] 張君, 趙海, 周艷. Internet路由級節點的度與核數的關系[J]. 東北大學學報(自然科學版), 2008, 29(5): 653-656.ZHANG J, ZHAO H, ZHOU Y. Relationship between degree and core number of internet nodes at router level[J]. Journal of Northeastern University(Natural Science), 2008, 29(5): 653-656.

[11] CHEN Q, CHANG H, GOVINDAN R, et al. The origin of power laws in Internet topologies revisited[A]. Proceedings of IEEE INFOCOM Conference[C]. New York, USA, 2002. 608-617.

[12] 張國強,張國清.Internet網絡的關聯性研究[J]. 軟件學報, 2006,17(3): 490-497.ZHANG G Q, ZHANG G Q. Research on Internet correlation[J].Journal of Software, 2006,17(3):490-497.

[13] HAMELIN A, LGNACIO J, LUCA D A, et al. Alessandro V k-core decomposition: a tool for the visualization of large scale networks[EB/OL]. http://arxiv.org/abs/cs. NI/0511007, 2005.

[14] Routeviews project [EB/OL]. http://www.routeviews.org,2008.

[15] DONNET B, FRIEDMAN T. Internet topology discovery: a survey[J].IEEE Communications Surveys & Tutorials, 2007, 9(4): 56-69.

[16] CAIDA[EB/OL]. http://www.caida.org,2008.

[17] MAHADEVAN P, KRIOUKOV D, FOMENKOV M, et al. The internet AS-level topology: three data sources and one definitive metric[EB/OL]. http://www.caida.org/outreach/papers/2006/as topology/as topology. pdf, 2006

[18] 張國強, 張國清. 互聯網 AS級拓撲的局部聚團現象研究[J]. 復雜系統與復雜性科學,2006,3(3):34-41.ZHANG G Q , ZHANG G Q. Research on local clustering of the Internet AS level topology[J]. Complex Systems and Complexity Science, 2006,3(3):34-41.

[19] NEWMAN M E J. Assortative mixing in networks[J]. Physical Review Letters, 2002, 89(20):8701-8704.

[20] ZHANG G Q, ZHANG G Q, YANG Q F, et al. Evolution of the Internet and its cores[J]. New Journal of Physics, 2008, 10(12):3027-3038.

[21] LIANG T, CHEN P Z, DA N S, et al. Universal scaling behavior of clustering coefficient induced by deactivation mechanism[J]. Physical Review E, 2006, 74(4): 3-10.