一種改進的關聯規則算法在就業管理信息系統中的應用研究

周 賢

(湖南第一師范學院招生就業處，湖南長沙410002)

一種改進的關聯規則算法在就業管理信息系統中的應用研究

周 賢

(湖南第一師范學院招生就業處，湖南長沙410002)

隨著高校畢業生就業制度的改革和高等教育規模的迅速擴大，高校畢業生的數量迅速增加，高等教育的決策者很想知道高等教育學科專業結構、辦學基本條件與學生就業之間的關系，以判斷高等教育是否適應社會需求。以高校畢業生就業信息數據為研究對象，將一種改進的關聯規則算法應用于就業信息數據分析，希望從大量積累的歷史就業信息數據中挖掘出有意義的規則，以便以就業為導向，提高高等教育質量，提高學生就業率。

關聯規則;就業管理;信息系統

隨著計算機技術的發展，我國不少單位的管理工作都向信息化方向轉變。比如就業管理方面的信息系統已經在不少高校投入運行，而且經過若干年的應用，系統積累了非常重要的就業管理方面的數據。但就目前所使用的就業管理信息系統而言，一般只是提供一些簡單的功能，比如:信息錄入、信息查詢以及信息的統計等。隨著就業信息量的增加，如何從其中挖掘出有效的規則，并進一步指導高校教學以及就業管理就成為一個值得關注的問題。也就是說，通過數據挖掘技術，從就業管理信息系統的數據中挖掘出知識，從而預測未來［1］。

尤其是最近幾年，我國高校規模不斷增大，畢業生就業制度也有了一定的變化，每年畢業生數量呈大幅度增長的趨勢，高校教育也由原來的精英化教育逐漸轉變成大眾化教育。這時，一個關鍵問題就顯現出來了。那就是這么多的大學生涌入社會，如何保證這些學生都能就業就成為亟待解決的問題。我國政府、高校以及企事業單位都在努力緩解就業壓力。高校領導層也認識到了就業率與教學專業結構、辦學基本條件等之間的關系，但只能借助于挖掘技術，才能實現以就業為導向，提取合理性的規則，從而提升高校教育水平，促進學生就業率的提高。作者提出了一種改進的關聯規則看法:希望從就業信息數據中挖掘出有意義的規則。

一 關聯規則Apriori算法的基本思想

關聯規則挖掘在數據挖掘中是一個重要的課題，最近幾年已被業界所廣泛研究。而Apriori算法則是關聯規則中的一個經典算法。該算法能夠有效生成候選測試規則。其中，算法可以在K－項目集的基礎上生成(K+1)－項目集。首先，算法生成頻繁1－項目集所對應的集合，可以記為L1。在L1集合的基礎上再生成頻繁2－項目集的集合，可以記為L2，并再次在L2的基礎上生成L3，不斷按照這樣的規則進行循環處理，直到最終生成頻繁K－項目集。需要注意的是，生成一個Lk都必須經過一次數據庫的掃描處理［2］。

Apriori算法屬于層次化算法的范疇，實現過程也比較簡單。但存在的關鍵問題是:Apriori算法每次生成項目候選集的時候都需要對數據庫進行一次掃描操作，當數據庫比較大，也就是對應的候選集比較大時，Apriori算法會花費大量時間在數據庫的掃描操作上，從而直接導致Apriori算法在時間上的開銷過大。另外，由于數據庫中的數據并不是不變的，隨著應用的深入，數據庫中的數據也在不斷增加中，而Apriori算法在運行時會涉及到頻繁項目集以及關聯規則的生成。這里為了挖掘結果的有效性，必須對這些增加的數據再次進行Apriori算法挖掘，這也表示之前挖掘出來的頻繁項目集以及關聯規則是無效的，這樣將明顯不利用于關聯規則的高效挖掘［3］。同時，如果數據庫的規模大于主存的時候，該Apriori算法的不足之處越明顯，效率也會受到更大的影響。

二 關聯規則Apriori算法的優化

從Apriori算法分析中，不難發現，Apriori算法生成一次頻繁集，都會執行數據庫掃描操作來判斷候選頻繁項目集是不是屬于頻繁項目集。在實際的執行過程中，有些項明顯不屬于頻繁項目集的，但Apriori算法仍然要去掃描數據庫，這顯然是影響了Apriori算法的效率，為避免這些不必要的掃描操作還需要進一步進行研究。本文提出關聯規則挖掘的改進模式，在Apriori改進算法中涉及到的關鍵術語定義如下:

(一)信息系統的定義

信息系統可以用S={U，I，F}加以表示，所有對象的非空有限集合用U={X1，X2，…，Xp}加以表示，屬性的非空有限集合用I={I1，I2，…，Im}加以表示，我們也可以稱之為屬性集。

(二)分辨矩陣的定義

信息系統用S={U，I，F}加以表示，定義映射φi:Vi→{0，1}如下:

(三)分辨向量的定義

若Dj稱為項 Ij的分辨向量［4］。

三 Apriori優化算法的偽碼描述

基于分辨矩陣的關聯規則Apriori算法的優化思想描述如:

Stepl:錄入信息系統，同時設置最小支持度。

Step2:對數據庫進行掃描操作，并產生對應的分辨矩陣D。

Step3:由分辨矩陣生成頻繁1－項目集，同時將K設置成2。

Step4:根據Lk－1中的頻繁k－1項目集產生頻繁K－項目集，并將頻繁K－項目集命名為集合R。

Step5:根據集合R，產生對應的項集下標集W。

Step6:對W中每一個下標Wi，計算下標集L'(Wi)，若存在Wi∈W，使得L'(Wi)≠Φ，則將Wi從W中刪去，并加入L'中。

Step7:對剪枝后的W中的每一個下標Wi，生成對應的分辨向量DWi，計算支持度計數，如下所示:

若 support－count(Rwi)＜ min－sup×|D|，則將Wi從W中刪去，并加入到L'中。

Step8:若W≠Φ，則根據下標集W中的每一個下標，生成集合R所相應的項集，并生成K－項目集，用Lk加以表示，令K=K+1轉至Step4，否則Step9。

Step9:輸出分辨矩陣中符合最小支持度的頻繁目集，用L=∪KLK加以表示。

四 關聯規則改進算法在就業管理信息系統中的應用

Apriori優化算法的思想就是利用Lk－1中的k－1項集連接生成K－項集的集合R，最終生成分辨矩陣D。那么針對就業信息，根據Apriori優化算法的思想，首先應找出學生就業信息系統的頻繁一維謂項集，然后在頻繁一維謂項集的基礎上，發現所有的頻繁k維謂項集，從而產生學生就業信息系統分辨矩陣所對應的關聯規則。由此可見關于多維頻繁謂詞集的生成是核心內容。因此，應用流程的核心就是如何由頻繁K－謂項集求頻繁K+1謂項集，我們可以借助于函數的遞歸調用來實現，應用的實現過程如下:

算法開始執行后，第一步先找到頻繁1－項目集，也就是頻繁一維謂詞集;第二步在頻繁1－項目集的基礎上，生成頻繁二維謂詞集，由此循環，生成最終的頻繁k維謂詞集。比如:針對就業管理信息中的“專業英語”字段，算法將其定義了一維頻繁謂詞，則生成的二維頻繁謂詞就可以是“專業 －英語”、“生源地 －長沙”。當該二維頻繁謂詞的相關計數值滿足一開始設定的最小支持度，則可以生成三維頻繁謂詞:“專業 － 英語”、“生源地 － 長沙”、“綜合測評 －高”。

但是，如果該二維頻繁謂詞的相關計算值并不滿足一開始設定的最小支持度，則凡是包括“專業－英語”、“生源地－長沙”的相關模式是不再被掃描的。關聯規則挖掘算法就是會其他的二維頻繁項集進行計數，比如:“專業 －英語”、“生源地 －湘潭”，然后重復上面的比較操作。根據上述的步驟進行不斷的頻繁謂詞添加后綴并判斷，最終生成所有的頻繁k維謂項集。

Step1:與就業管理信息系統的數據進行連接操作，查詢定位相關信息，涉及到關鍵表的一些屬性維以及記錄數等等信息。

Step2:K=m=n=1，求一維頻繁謂詞項集，N=總屬性維數。

Step3:針對于就業管理信息系統中的一維頻繁謂詞集，可以選擇其中的第m個屬性作為起始屬性，并根據該屬性的n個成員作為頻繁維謂詞集，如果k的取值是1，那么當前的頻繁維謂詞集就是1維的。

Step4:將頻繁維謂詞項與數據庫表第i+1個屬性維中的第j個成員進行連接操作，產生對應的K+1謂詞項，同時對數據庫進行掃描并生成該謂詞項的計數。

Step5:判斷計數與一開始設定的最小支持度之間的大小關系。如果大于，則將K+1謂詞項作為當前頻繁維謂詞項，i及k進行步長為1的遞增;否則，計算j是否大于第i+1個屬性維中的成員總數，如果是，將i進行步長為1的遞增，j=1。

Step6:計算n是否大于第m個屬性維中的成員總數。如果是，則m++，n=1;反之，轉至Step3;

Step7:計算m是否大于N，如果是，則終止算法流程。反之，轉至Step3。

五 關聯規則改進算法在就業管理信息系統中的應用實例

某高校計算機科學與技術專業每學期都要統計學生的就業分配情況，現隨機抽取400名學生的畢業分配情況，將學號、數據結構課程成績、大學英語成績、文化課測評成績、綜合測評成績、行業、收入等7項數據輸入數據庫(如表1所示)。我們將找出數據結構課程成績和大學英語成績對就業行業的影響，文化測評成績和綜合測評成績哪個對收入的影響更大。

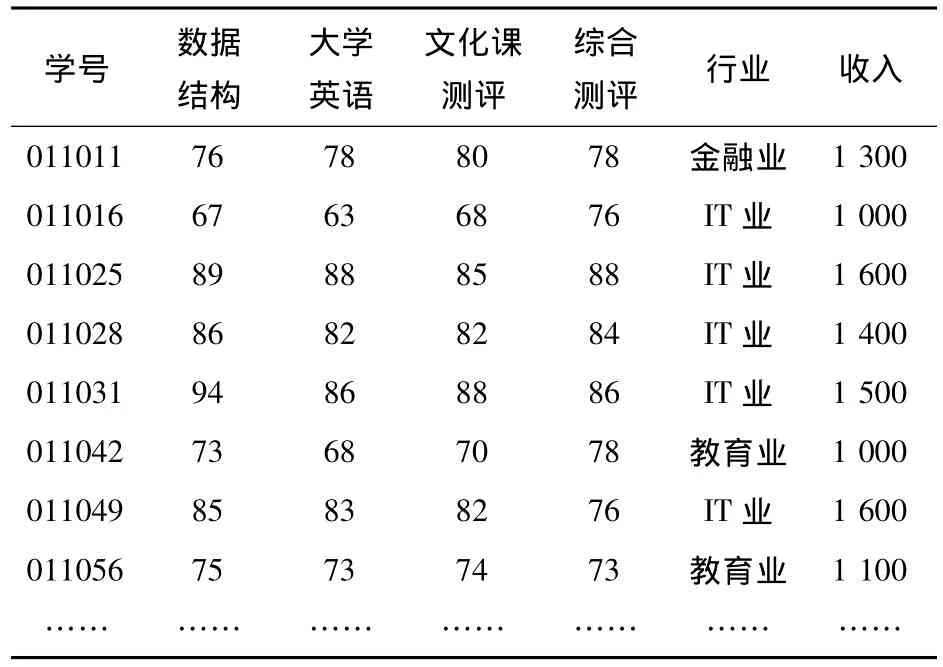
表1 就業評價信息表

在上表中，數據結構成績、大學英語成績、文化課測評成績、綜合測評成績及收入都是樹立屬性(非離散屬性)，這里，我們將其離散化。首先，對數據結構成績、大學英語成績、文化課測評成績、綜合測評成績采用統一的量化標準，分為兩個等級，成績高于85分的為良好，低于85分的為一般。將收入也量化為兩個值，高于1 500的為高收入，低于1 500的為低收入。

將表中的相關記錄進行編碼，將就業評價信息表中的記錄以 i1，i2，…，i8進行編碼。

輸入:就業評價信息表;輸出:分辨矩陣表。

(1)挖掘頻繁1－項集L1

輸入:分辨矩陣表和最小支持度min－sup=0．25

輸出:L1={i1，i2，…，i8}

(2)挖掘頻繁項集L

輸入:L14L

輸出:L=k∪=1k，其中 L1同上

L2={i14，i16，i17，i34，i45，i46，i47，i48，i56，i67}，

L3={i146，i147，i167，i456，i467}，

［1］閆 禹．數據挖掘技術在高校學生就業指導決策中的運用［J］．沈陽工業大學學報，2007，29(3):344－346．

［2］宋 波，李妙妍，趙 晶．利用泛型DAO模式改進輕量級J2EE架構［J］．計算機工程與設計，2009，30(24):5663－5666．

［3］劉美玲，李 熹，李永勝．數據挖掘技術在高校教學與管理中的應用［J］．計算機工程與設計，2010，31(5):1130－1133．

［4］李燚琳，張 璞．數據挖掘技術在教務信息挖掘系統中的應用［J］．制造業自動化，2010，32(4):200－203．

L4={i1467}。

(3)挖掘關聯規則集R

輸入:L，最小置信度min－conf=0．75

輸出:R1:i1i46(sup=0．3061，conf=0．789 5)

R1:i1i46(sup=0．2959，conf=0．878 8)

R2:i7i14(sup=0．2959，conf=0．763 2)

R3:i1i47(sup=0．2653，conf=0．787 9)

R4:i7i16(sup=0．2959，conf=0．878 8)

R5:i7i46(sup=0．2653，conf=0．896 6)

R6:i67i14(sup=0．2653，conf=0．812 5)

R7:i47i16(sup=0．2653，conf=0．896 6)

R8:i17i46(sup=0．2653，conf=0．812 5)

搜索原始數據庫，得到滿足最小支持度和最小置信度的關聯規則:

(1)數據結構(良好)。行業(IT):數據結構成績良好的學生從事IT行業。該規則的支持度為28%，置信度為72%。

(2)綜合測評(良好)。收入(高收入):綜合測評成績良好的學生的工資收入比較高。該規則的支持度為24%，置信度為81%。

(3)文化課測評(良好)。收入(高收入):文化課測評成績良好的學生的工資收入比較高。該規則的支持度為25%，置信度為74%。

規則(l)說明數據結構成績好的學生的實際編程能力很強，很適合從事IT行業，大部分學生的就業行業都是IT業。規則(2)和規則(3)說明測評成績高的學生的工資收入比較高。規則(2)的置信度高于規則(3)，且規則(3)的支持度高于規則(2)的支持度，這說明綜合測評高的學生獲得高工資的可能性更大，也就是在找工作的過程中，用人單位更注重綜合能力。因此，在培養學生的過程中，多注重綜合能力的培養。

G421

A

1674－5884(2011)10－0032－03

2011－07－18

周 賢(1981－)，男，湖南湘潭人，碩士生，政工師，主要從事高教管理研究。

(責任編校 楊鳳娥)