一類非線性二層規劃問題的神經網絡方法

洪云飛

(長江大學期刊社；長江大學信息與數學學院，湖北 荊州 434023)

呂一兵

(長江大學信息與數學學院，湖北 荊州 434023)

一類非線性二層規劃問題的神經網絡方法

洪云飛

(長江大學期刊社；長江大學信息與數學學院，湖北 荊州 434023)

呂一兵

(長江大學信息與數學學院，湖北 荊州 434023)

研究了下層為凸規劃的一類非線性二層規劃問題的神經網絡方法。在下層問題為凸規劃的情況下,將下層問題用其K-T最優性條件代替，從而把原二層規劃轉化為單層非線性規劃；構造該單層規劃的罰函數，提出求解該類規劃問題的神經網絡方法。數值試驗結果表明該方法是可行和有效的。

非線性二層規劃；罰函數；K-T最優性條件；神經網絡

在對多層規劃的研究中，二層規劃是一個重要的研究對象。二層規劃研究的是具有2個層次系統的規劃與管理問題，上層決策者只是通過自己的決策去指導下層決策者，并不直接干涉下層的決策；而下層決策者只需要把上層的決策作為參數，它可以在自己的可能范圍內自由決策。二層規劃的基本形式為：

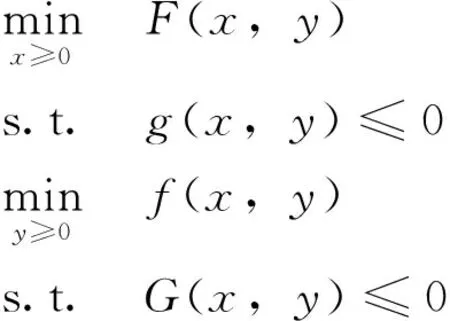
式中，x、y分別稱為上下層變量；F、f分別稱為上下層目標函數；g、G分別稱為上下層約束函數。當F、f、G、g全為線性函數, 則稱為線性二層規劃；否則稱為非線性二層規劃。

一般來說，求解二層規劃問題是非常困難的，文獻[1]指出線性二層規劃是一個Np-hard問題，文獻[2-4]對此結論給出了證明。對于一般的非線性二層規劃問題, 文獻[5-6]提出了基于下層問題的K-T最優性條件的求解方法。下面筆者主要研究F、f、G、g連續可微且f、G關于變量y是凸函數的一類非線性二層規劃問題：鑒于文獻[5-6]中的方法，將下層問題用其K-T最優性條件代替，從而將原二層規劃化為單層非線性規劃, 構造該單層規劃的罰函數，進而提出求解該類規劃問題的神經網絡方法。

1 非線性二層規劃問題的轉化

考慮如下線性約束的非線性二層規劃問題：

其中，x∈Rn，y∈Rm，F:Rn×m→R1，f:Rn×m→R1，P∈R(n+m)×(n+m)，c∈Rn，d∈Rm，Q∈Rm×m，D∈Rm×n，b∈Rm，A∈Rq×n，B∈Rq×m，r∈Rq。

定義1對于線性二層規劃問題，稱集合：

S={(x,y)|Ax+By-r≤0,x≥0,y≥0}

為其約束域。

對于固定的x，當下層問題滿足Slater條件，由凸規劃的最優性理論可知，下層規劃問題可以轉化等價如下Kuhn-Tucker最優性條件穩定點問題：

Qy+Dx+b+λTB=0λT(Ax+By-r)=0λ≥0Ax+By-r≤0

(2)

式中，λ=(λ1,…,λq)T是廣義拉格朗日乘子。用式(2)替換式(1)中的下層問題得：

記h(x,y,λ)=(Qy+Dx+b+λTB,λT(Ax+By-r))T，則問題(3)可簡寫為下格式：

2 非線性二層規劃問題的神經網絡模型

定義2問題(4)的罰函數[7]定義為：

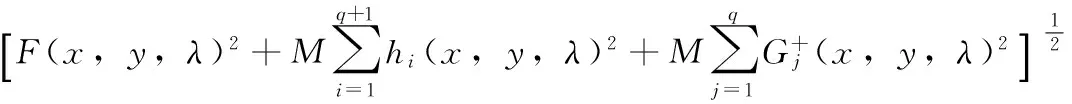
(5)

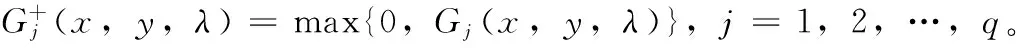
由此問題(4)可以對應轉化為如下罰函數優化問題：

記X=(x,y,λ)T，由式(5)則可定義其能量函數[7,8]為：

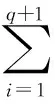
(6)

根據神經網絡理論，將優化設計變量與神經元輸出相對應，構造神經網絡的非線性微分方程(動力系統)為：

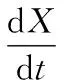
(7)

由式(6)和式(7)可得到能量函數隨時間的變化率為：

(8)

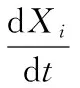
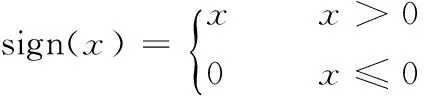
因此，式(7)可以具體化為：

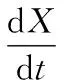
(9)

定理1若X*是網絡動力系統(7)或(9)在罰因子M下的平衡點，對于X≠0有E(X)≠0，則X*是網絡動力系統(7)或(9)的穩定點，且為罰函數優化問題的局部最優點。若X*是罰函數優化問題的一個最優解，則X*是網絡動力系統(7) 或(9)的在罰參數M下的平衡點。

定理1前一部分由式(8)可知是成立的，后一部分顯然成立。

3 數值試驗

考慮其理論最優解為如下的非線性二層規劃問題:

使用定步長四階龍格庫塔法求解上述問題的神經網絡動態方程(9)。選取初值為(x,y,λ1,λ2,λ3)=(5，5，1，1，1)，罰因子M=10000，步長為10-5，得到圖1。

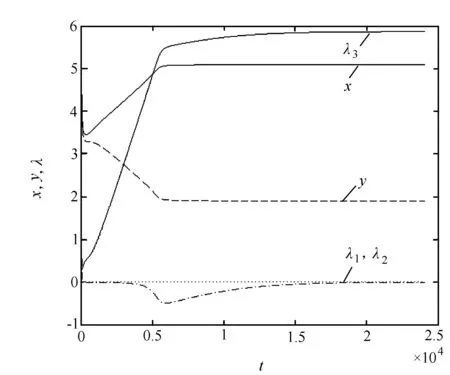
圖1 x、y、λ隨時間的變化曲線

從圖1中可以看到曲線最終都達到穩定狀態，由該方法得到最終的計算結果為(x,y,λ1,λ2,λ3)=(5.104，1.891，0.000，-0.000，5.870)，所以用神經網絡方法求得的優化解為(x,y)=(5.104，1.891)。數值試驗結果表明，神經網絡最終達到穩定狀態，可以得到非線性二層規劃問題的最優解。

4 結 語

給出了下層為凸規劃的一類非線性二層規劃問題的神經網絡方法，該算法的設計比較簡單，易于編程實現，同時值得注意的是利用罰函數構造神經網絡模型使得系統變量較少，同時可增大罰因子的值以加快網絡的收斂速度。但是在數值試驗的過程中，選取不同的初值對神經網絡的最終穩定狀態有不同的影響，尤其當選取決策變量的初值較小時，將得不到最優解的穩定狀態，而且罰因子過小起不到懲罰作用，過大又受機器性能影響。因此，該非線性二層規劃問題的神經網絡方法的全局穩定性研究方面以及初值有待進一步深入。

[1]Jeroslow R.The polynomial hierarchy and a simple model for competitive analysis[J].Mathematical programming，1985，32(2)：146-164.

[2]Ben-Ayed O，Blair C E.Computational difficulties of bilevel linear programming[J].Operations Research，1990，38(3)：556-560.

[3]Bard J.Some properties of the bilevel programming problem [J].Journal of Optimization Theory and Applications.1991，68(2)：371-378.

[4]Hansen P，Jaumard B，Savard G.New branch and bound rules for linear bilevel progra-mming [J].SIAM Journal scientific and statistical computing，1992，13(5)：1194-1217.

[5] Lv Yibing，Hu Tiesong，Wang Guangmin，et al.A penalty function method based on Kuhn-Tucker condition for solving linear bilevel programming[J].Applied Mathematics and Computation，2007，188(1)：808-813.

[6]呂一兵，陳忠，萬仲民，等.非線性-線性規劃問題的罰函數方法[J].系統科學與數學，2009，29(5)：630-636.

[7]孟志青，胡奇英，楊曉琪.基于精確罰函數的一類廣義非線性神經網絡模型[J].自動化學報，2003，29(5)：755-760.

[8]任麗君.基于罰函數法的神經網絡優化設計研究[J].紹興文理學院學報，2006，26(10)：36-39.

[編輯] 李啟棟

10.3969/j.issn.1673-1409.2011.12.002

O224

A

1673-1409(2011)12-0004-03