形式函數的可微性與共軛解析性
吳 曉,徐士河
(肇慶學院數學與信息科學學院,廣東 肇慶 526061)
形式函數的可微性與共軛解析性
吳 曉,徐士河
(肇慶學院數學與信息科學學院,廣東 肇慶 526061)
從復變函數的復形式出發,研究其可微和解析的充要條件,進而得出其共軛可微和共軛解析的條件,并給出了判定形式函數的可微性和解析性的應用。
形式函數;形式可微;解析; C-R條件
復變函數可微的條件是一個重要研究內容。現行教材中已對復變函數的可微性進行了討論,如文獻[1-2]研究了直角坐標系下的C-R方程,得到了函數可微的條件。復變函數共軛解析的前提是函數共軛可微,因而研究復變函數共軛可微的充要條件就尤為重要。下面,筆者定義了形式函數的形式導數與形式微分,根據復變函數可微的方法去研究了復變函數共軛可微的性質,從而得出形式函數的可微和解析條件。
1 預備知識
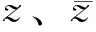
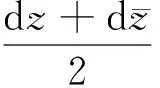
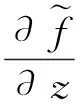
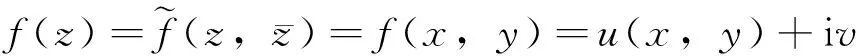
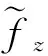
(1)
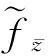
(2)
從而有:


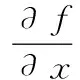

定義3若滿足:

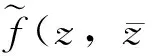
2 形式函數的解析性
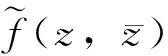
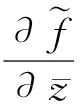
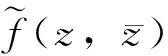
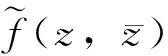
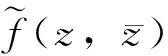
證明:

(3)
則代入式(3)得:
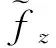
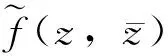
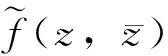
證明由于:
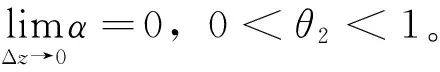
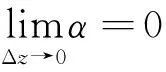
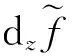
由解析函數的定義和定理3,可得到刻畫形式函數在區域D內解析的定理4。
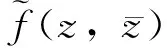
3 形式函數的共軛解析性

這時稱函數w=f(z)于點z共軛可導或可微。
引理2[4]設函數w=f(z)=u(x,y)+iv(x,y)在區域D內有定義,則函數f(z)在點z=x+iy∈D共軛可微的充要條件是:
(1)二元函數u(x,y)、v(x,y)在點(x,y)可微;
(2)u(x,y)、v(x,y)在點(x,y)滿足共軛解析條件:
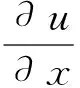
于是由引理2知,類似定理2容易得出以下結論。

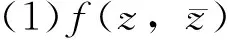

由于二元函數的可微性可以通過偏導數連續判斷出來,因而可得到下述推論。

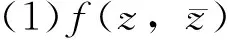


[1]鐘玉泉.復變函數論[M].第3版.北京:高等教育出版社,1978:52-71.
[2]杜應雪,許小艷.復變函數的可導性與解析性[J].中國科技信息,2006(13):272-287.
[3]譚小江,伍勝鍵.復變函數簡明教程[M].北京:北京大學出版社,2006:21-22.
[4]王見定.半解析函數共軛解析函數[M].北京:北京工業大學出版社,1988.
[編輯] 洪云飛
10.3969/j.issn.1673-1409.2011.12.004
O174.5
A
1673-1409(2011)12-0009-03

