例談方程整數解問題的解法

●

(新星學校 浙江蒼南 325800)

例談方程整數解問題的解法

●易永彪

(新星學校 浙江蒼南 325800)

在各類數學競賽和高中自主招生考試中,二次方程整數解問題備受關注.它將古老的整數理論與傳統的初中數學知識相結合,涉及知識面寬、范圍廣,往往需要靈活地運用相關概念、性質、方法和技巧,綜合性強,對學生的能力有較高的要求.本文將對方程整數解問題的解法與基本策略作一探索,旨在拋磚引玉.

1 巧用因式分解

例1方程-m4+4m2+2nm2+2n+5=0的正整數解有

( )

A．1組 B．2組 C．4組 D．無窮多組

(2009年浙江省溫州中學自主招生考試試題)

解原方程可化為

m4-(2n+4)m2-(2n+5)=0,

可得

[m2-(2n+5)](m2+1)=0.

因為

m2+1gt;0,

所以

m2=2n+5.

(1)

因此m為奇數,不妨設m=2k+1(k為自然數),代入式(1)得

k2+k-1=2n-2.

因為k2與k的奇偶性相同,所以k2+k-1是奇數,不能被偶數整除,因此2n-2只能為1，從而

n=2,m=3,

原方程只有1組正整數解.故選A.

例2已知方程a2x2-(3a2-8a)x+2a2-13a+15=0(a≠0)至少有一個整數根,求整數a的值.

解已知方程經整理得

[ax-(a-5)][ax-(2a-3)]=0,

解得

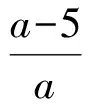
由題意知a為整數,因此a的取值為

1,3,5,-1,-3,-5.

評注分析方程的形式特征,可采用因式分解、求根公式等方法求得方程的根,再結合整除性質、奇偶性等進行求解.

2 巧用判別式

例3設m為整數，且4lt;mlt;40，方程x2-2(2m-3)x+4m2-14m+8=0有2個相異整數根，求m的值及方程的根．

解由題意知

Δ=4(2m-3)2-4(4m2-14m+8) =4(2m+1).

對4lt;mlt;40的整數m，要使Δ=4(2m+1)為完全平方數的m只能取為12和24，而

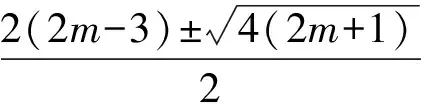
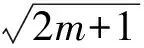
因此當m=12時，x1=16,x2=26；當m=24時，x1=38,x2=52.

例4已知p為質數,使二次方程x2-2px+p2-5p-1=0的2個根都是整數,求出p的所有可能值.

解由已知整系數二次方程有整數根,得

Δ=4p2-4(p2-5p-1)=4(5p+1)

為完全平方數,從而5p+1為完全平方數.因此可設5p+1=k2.注意到p≥2,因此k≥4,且k為整數，于是

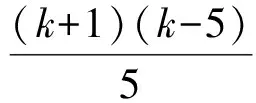
那么k+1與k-1中至少有一個是5的倍數,即k=5a±1(a為正整數),因此

5p+1=(5a±1)2=25a2±10a+1,

解得

p=a(5a±2).

由p為質數,5a±2gt;1,可知a=1,因此

p=3或p=7.

當p=3時,原方程變成x2-6x-7=0,解得

x1=-1,x2=7；

當p=7時,原方程變成x2-14x+13=0,解得

x1=1,x2=13.

故p=3或p=7.

評注因為整系數二次方程有整數根,所以Δ必為完全平方數．當問題比較復雜時，可通過恰當設元、引入參數,利用因式分解、數論等方法求解．

3 巧用韋達定理

例5求使關于x的方程kx2+(k+1)x+k-1=0的根都是整數的k值.

解當k=0時,x=1符合題意.

當k≠0時,設方程kx2+(k+1)x+k-1=0的2個根為x1,x2(x1≤x2),因此

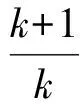
(2)

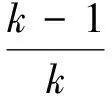
由式(2)-式(3)得

x1+x2-x1x2=-2,

于是

(x1-1)(x2-1)=3,

解得

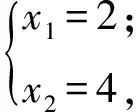
從而

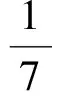
綜上所述,滿足題意的k值為

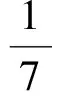
例6已知關于x的一元二次方程x2+cx+a=0的2個整數根恰好比方程x2+ax-b=0的2個根都大1,求a+b+c的值.

(2011年全國初中數學競賽試題)

解設方程x2+ax+b=0的2個根為α,β,其中α,β為整數,且α≤β,則方程x2+cx+a=0的2個根為α+1,β+1.由題意得

α+β=-a,(α+1)(β+1)=a,

兩式相加得

αβ+2α+2β+1=0,

即

(α+2)(β+2)=3,

解得

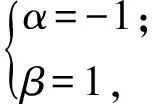
又因為

a=-(α+β),b=αβ,c=-[(α+1)+(β+1)],

所以a=0,b=-1,c=-2；或a=8,b=15,c=6,

故

a+b+c=-3或a+b+c=29.

評注從根與系數的關系式中消去參數,可得關于兩根的不定方程,借助因數分解、因式分解求解.

4 巧用主元更換

例7若關于x的方程ax2+2(a-3)x+(a-13)=0至少有一個整數根,求非負整數a的值.

ax2+2(a-3)x+(a-13)=0,

化簡得

(x+1)2a=6x+13,

因此

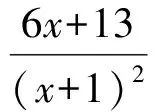
即

x2-4x-12≤0,

解得

-2≤x≤6.

因為x為整數,x≠-1,所以x的值可取為

-2,0,1,2,3,4,5,6.

把x分別代入求得a的值,且a為非負整數,可得a的值為1,13.

例8已知

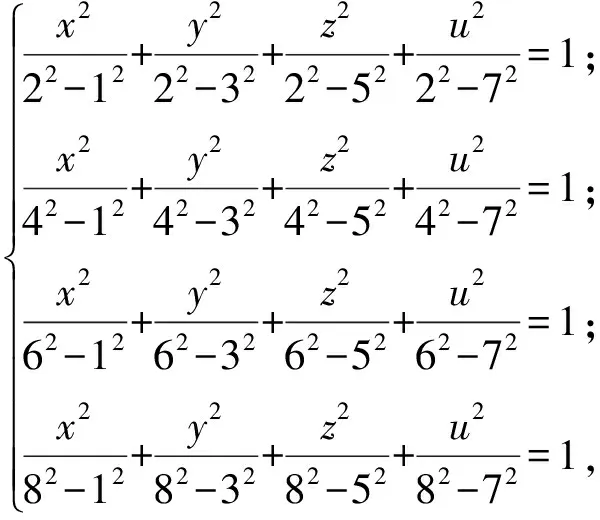
試求x2+y2+z2+u2的值．

解本題為四元二次方程，直接求解相當困難，但各個方程結構完全相同，因此可考慮更換主元．原方程與

等價，這里t的值為4,16,36,64.

當t≠1,9,25,49時,方程(4)與

(t-9)(t-25)(t-59)x2+

(t-1)(t-25)(t-49)y2+

(t-1)(t-9)(t-49)z2+

(t-1)(t-9)(t-25)u2-

(t-1)(t-9)(t-25)(t-49)=0

(5)

等價.而式(5)是關于t的四次方程，至多有4個根.因為t=4,16,36,64是式(4)的根，所以必為式(5)的4個根，即式(5)等價于

(t-4)(t-16)(t-36)(t-64)=0.

對比展開式t3的系數可得

x2+y2+z2+u2+1+9+25+49=

4+16+36+64，

故

z2+y2+z2+u2=36．

評注當一個方程按常規意義下的求解比較困難時,可以通過觀察方程的結構特征，選擇更換主元，使方程次數和結構形式發生變化，從而轉化為一個容易求解的問題．