關(guān)于“點(diǎn)共圓”問題的普及

●

(鎮(zhèn)海蛟川書院 浙江寧波 315200)

關(guān)于“點(diǎn)共圓”問題的普及

●劉清泉

(鎮(zhèn)海蛟川書院 浙江寧波 315200)

“點(diǎn)共圓”是數(shù)學(xué)競(jìng)賽中的一項(xiàng)重要內(nèi)容，三角形、四邊形中的很多內(nèi)容都與之關(guān)聯(lián).但隨著新課程改革對(duì)邏輯推理要求的降低，特別是初中教材中對(duì)“點(diǎn)共圓”涉及的不多，在數(shù)學(xué)競(jìng)賽中與“圓”相關(guān)內(nèi)容的比例也在降低.此時(shí),與“點(diǎn)共圓”的相關(guān)內(nèi)容和相關(guān)方法更顯得重要.本文力求用幾個(gè)平面幾何中相關(guān)的定理知識(shí)將這一內(nèi)容作一有機(jī)的整合.

1 基礎(chǔ)知識(shí)

如圖1～3，A，B，C，D四點(diǎn)共圓，得到如下3個(gè)結(jié)論:

(1)∠A=∠D；

(2)∠A+∠C=180°；

(3)∠PAD=∠C.

分別概括為：①同弦同側(cè)張角相等；②同弦異側(cè)張角互補(bǔ)；③外角等于內(nèi)對(duì)角.

圖1 圖2 圖3

在圖1和圖3中,分別可得：

(4)PA·PC=PB·PD；

(5)PA·PB=PC·PD.

即“圓冪定理”中的“相交弦定理”(記為④)和“割線定理”(記為⑤).同時(shí)，不難證明：定理①～⑤的逆命題也是真命題.原命題是“四點(diǎn)共圓”的性質(zhì)，其逆命題可作為“四點(diǎn)共圓”的判定.另外，一些特殊的四邊形，如矩形、等腰梯形、一組對(duì)角都為直角的四邊形是圓內(nèi)接四邊形，常常作為解題,特別是添加輔助線的切入點(diǎn).

2 知識(shí)應(yīng)用

2.1 費(fèi)馬點(diǎn)(三角形每個(gè)內(nèi)角都小于120°的費(fèi)馬點(diǎn))

例1△ABC的每個(gè)內(nèi)角都小于120°，在△ABC的內(nèi)部找一點(diǎn)P，使得PA+PB+PC最小.

分析為求線段和的最小值，先將“丫”字形的3條線段PA，PB，PC,通過旋轉(zhuǎn)變換轉(zhuǎn)化為一條折線段.

解如圖4，將△APB繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)60°得到△A′P′B.連結(jié)PP′，易證△PBP′為正三角形，從而

PB=P′P.

又由PA=P′A′，得

PA+PB+PC=A′P′+P′P+PC,

即對(duì)于△ABC內(nèi)的任意一點(diǎn)P，PA，PB，PC的長度之和等于2端A′，C固定的折線A′P′PC的長，當(dāng)且僅當(dāng)A′，P′，P，C共線時(shí)，其值最小.此時(shí)由

∠A′P′B+∠BP′P=∠BPP′+∠BPC=180°

及

∠BP′P=∠BPP′=60°，

得

∠A′P′B=∠BPC=120°，

從而

∠APB=∠BPC=∠CPA=120°.

此時(shí)點(diǎn)P稱為△ABC的“費(fèi)馬點(diǎn)”(又稱“正等角中心”).

圖4 圖5 圖6

怎樣用直尺、圓規(guī)來確定這個(gè)點(diǎn)呢？

如圖5，以△ABC的邊BC，CA為邊向外作正三角形△BCA′，△CAB′.連結(jié)AA′，BB′交于點(diǎn)P，易證△ACA′≌△B′CB，因此

∠A′AC=∠BB′C，

得A，B′，C，P四點(diǎn)共圓，從而

∠A′PC=∠AB′C=60°，

∠BPA′=∠APB′=∠ACB′=60°，

得

∠BPC=120°.

同時(shí)由∠CPA+∠AB′C=180°,得

∠CPA=120°，

于是

∠APB=∠BPC=∠CPA=120°，

故AA′，BB′的交點(diǎn)即為“費(fèi)馬點(diǎn)”.

更進(jìn)一步探究，此時(shí)再以AB為一邊向外作正三角形△ABC′，連結(jié)AA′，BB′，CC′,這3條線共點(diǎn)嗎？

如圖6，將AA′，BB′，CC′三線共點(diǎn)轉(zhuǎn)化為點(diǎn)C，C′及AA′與BB′確定的交點(diǎn)P三點(diǎn)共線.連結(jié)CP，C′P.由∠APB+∠AC′B=180°，得A，P，B，C′四點(diǎn)共圓，從而

∠C′PB=∠C′AB=60°.

進(jìn)而由∠C′PB+∠BPC=180°，得C，P，C′三點(diǎn)共線，證畢.

對(duì)于論證三角形每個(gè)內(nèi)角都小于120°的費(fèi)馬點(diǎn)的其他方法,以及三角形有一個(gè)內(nèi)角不小于120°的費(fèi)馬點(diǎn)退化為120°的內(nèi)角頂點(diǎn)問題,在此不再贅述.

2.2 托勒密定理與逆定理

2.2.1 托勒密不等式

例2對(duì)于四邊形ABCD，恒有

AB·CD+BC·DA≥AC·BD.

簡(jiǎn)證如圖7，在四邊形內(nèi)取點(diǎn)E，使得

∠1=∠2，∠3=∠4，

得

△ABE∽△ACD，

從而

即

AB·CD=BE·AC.

∠BAC=∠EAD，

因此

△ABC∽△AED，

從而

得

BC·DA=DE·AC，

于是

AB·CD+BC·DA=BE·AC+DE·AC=

(BE+DE)·AC≥

BD·AC.

進(jìn)一步，當(dāng)且僅當(dāng)B，E，D共線時(shí)等號(hào)成立，此時(shí)圖中∠5=∠1.又∠1=∠2，得∠5=∠2，即A，B，C，D四點(diǎn)共圓.由此不難得到：在圓內(nèi)接四邊形ABCD中，有

AB·CD+BC·DA=AC·BD(托勒密定理)；

對(duì)于四邊形ABCD，若AB·CD+BC·DA=AC·BD，則這個(gè)四邊形內(nèi)接于一圓(托勒密定理的逆定理).

圖7 圖8

2.2.2 用托勒密不等式證明費(fèi)馬點(diǎn)

例3△ABC的每個(gè)內(nèi)角都小于120°，在△ABC的內(nèi)部找一點(diǎn)P，使得PA+PB+PC最小.

簡(jiǎn)證設(shè)點(diǎn)P為△ABC的正等角中心(即費(fèi)馬點(diǎn))，如圖8,作出△BPC的外接圓，并設(shè)AP交該圓于點(diǎn)P′.由△P′BC為圓的內(nèi)接三角形，可證

PP′=PB+PC，

因此

PA+PB+PC=AP′.

設(shè)Q為不同于點(diǎn)P的任意一點(diǎn)，由托勒密不等式得

QC·BP′+QB·CP′≥BC·P′Q，

即

QC+QB≥P′Q，

故

QC+QB+QA≥P′Q+QA≥AP′=

PA+PB+PC，

當(dāng)且僅當(dāng)Q為圓與AP′在三角形內(nèi)的交點(diǎn)，即點(diǎn)Q與點(diǎn)P重合時(shí),取到等號(hào).

2.3 九點(diǎn)圓

例4點(diǎn)O1，O2，O3分別為△ABC中邊BC，CA，AB的中點(diǎn)，點(diǎn)H為△ABC的垂心，點(diǎn)H1，H2，H3分別為高足，點(diǎn)D1，D2，D3分別為AH，BH，CH的中點(diǎn).求證：點(diǎn)O1，O2，O3，H1，H2，H3，D1，D2，D3九點(diǎn)共圓.

分析欲證多點(diǎn)共圓，常用的辦法有:

(1)圓的定義：到定點(diǎn)距離等于定長；

(2)先證四點(diǎn)共圓，再證其余的點(diǎn)在這個(gè)圓上；

(3)先分別證明幾組點(diǎn)共圓，再證明這幾個(gè)圓重合.

圖9

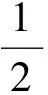
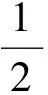
2.4 蝴蝶定理

(1)蝴蝶定理及常見證明方法.

例5在⊙O中，弦CD，EF過弦AB中點(diǎn)M，弦CF，DE分別交AB于點(diǎn)P，Q.求證：PM=QM.

方法1“軸對(duì)稱”法

分析如圖10，作直線OM(⊙O的對(duì)稱軸)，以O(shè)M為對(duì)稱軸作C的對(duì)稱點(diǎn)C′，則點(diǎn)C′在圓上.連結(jié)C′Q，可證△PMC≌△QMC′.又已知∠1=∠2，MC=MC′，可證∠3=∠4.由圓周角定理得∠3=∠5，即證∠4=∠5，故而轉(zhuǎn)化為C′，M，Q，E四點(diǎn)共圓的證明.

圖10 圖11

途徑1如圖11，連結(jié)CC′，C′E，易知CC′∥PQ，不難得到∠2=∠8=∠7.由C，D，E，C′四點(diǎn)共圓，得

∠6+∠7=180°，

從而

∠6+∠2=180°.

途徑2如圖12，連結(jié)C′E，延長C′M交⊙O于點(diǎn)D′，連結(jié)BD′，可得

∠2+∠6=180°.

注：以上2條途徑以“同線異側(cè)張角互補(bǔ)”作為落點(diǎn)得以證明，當(dāng)然也可以把“同線同側(cè)張角相等”(如圓周角∠EC′Q與圓內(nèi)角∠EMQ相等)作為落點(diǎn)得以證明.

圖12 圖13

方法2“相似”法

分析把一組對(duì)角都為直角的四邊形是圓內(nèi)接四邊形作為添加輔助線的切入點(diǎn).

簡(jiǎn)證如圖13，作OG⊥FC于點(diǎn)G，作OH⊥DE于點(diǎn)H.由垂徑定理得

連結(jié)OM,OP,OQ,MG,MH,易知

△FMC∽△DME，

得

因此

又∠F=∠D,得△FMG∽△DMH，故∠1=∠4.

由垂徑定理知OM⊥AB，又OG⊥FC，OH⊥FC，得O，G，P，M四點(diǎn)共圓，O，H，P，M四點(diǎn)共圓，從而

∠1=∠2，∠3=∠4，

即∠2=∠3，結(jié)合OM⊥PQ易證結(jié)論.

注：蝴蝶定理的證法很多，但在初中范圍內(nèi)這2種證法最易于接受.

(2)蝴蝶定理的推廣.

圖14 圖15

圖16 圖17

2.5 海倫公式的推廣

證明2S=ad·sin∠BAD+bc·sin∠BCD=

(ad+bc)·sin∠BAD.

由

BD2=a2+d2-2adcos∠BAD=

b2+c2-2bccos∠BCD=

b2+c2+2bc·cos∠BAD,

得

則

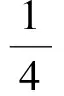
即

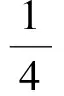
于是

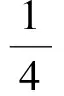
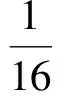
bc)-(a2+d2-b2-c2)]=

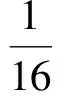
(b+c+d-a),

故

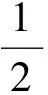
從以上內(nèi)容可以看出，“點(diǎn)共圓”在平面幾何

圖18

中廣泛存在且至關(guān)重要，平面幾何中的很多重要定理都與之相關(guān)，再譬如：(1)“法尼阿諾——許瓦茲問題”(在銳角△ABC的3邊各取一個(gè)點(diǎn)M,N,P，使△MNP的周長最短)中的光路三角形與高足三角形；(2)“米庫勒定理”(如圖18，延長凸五邊形ABCDE各邊得一五角星，它的5個(gè)三角形分別是△ABF，△BCG，△CDH，△DEI，△EAJ，它們的外接圓兩兩相交得到的不同于五邊形ABCDE頂點(diǎn)的5個(gè)交點(diǎn)為A′,B′,C′,D′,E′，求證：A′,B′,C′,D′,E′共圓)等.另外，一些“圓共點(diǎn)”的問題也可以轉(zhuǎn)化為“點(diǎn)共圓”的問題得以解決.