隨機事件的獨立性淺析

姚道洪，楊德志 (青島理工大學(臨沂)基礎課教學部，山東 臨沂 273400)

隨機事件的獨立性淺析

姚道洪，楊德志 (青島理工大學(臨沂)基礎課教學部，山東 臨沂 273400)

隨機事件的獨立性是概率論中特別重要的概念。從隨機事件獨立性的概念入手，多角度結合實例展開分析，闡述了隨機事件獨立性與互斥的關系，并結合條件概率與幾何概率對隨機事件獨立性的意義進行了探討。

隨機事件；獨立性；互斥；條件概率；幾何概率

1 隨機事件獨立性的定義

隨機事件的獨立性是概率論中特有的也是非常重要的一個概念。

定義1[1]2個隨機事件A與B，如果其中任何一個事件發生的概率不受另外一個事件發生與否的影響，則稱事件A與B是相互獨立的。

結合條件概率常常見到“事件B發生的概率不受事件A發生的影響”的對獨立性的解釋[2]，有時為了講的更清楚，也結合實例展開說明，如文獻[3]中講“顯然甲幣是否出現正面與乙幣是否出現正面是互不影響的”。其實“影響”2字文學色彩更濃一些，單是從此2字上是很難弄明白獨立性概念。定義1的缺點正如前面所說，有局恨性，不易理解，在此不加討論。

定義2[2]設A，B是2隨機事件，如果滿足等式：

P(AB)=P(A)P(B)

則稱事件A，B相互獨立，簡稱A，B獨立。

定義3[2]設A，B，C是3個隨機事件，如果滿足等式：

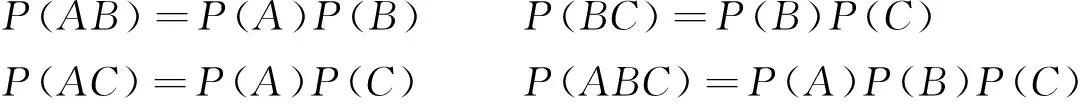
則稱事件A，B，C相互獨立。

對于以上定義，需注意以下幾點：

1)隨機事件的獨立性是指的事件概率的一種運算關系。從定義2中可以理解到，P(A)>0,P(B)>0時需滿足P(AB)=P(A)P(B)則稱A，B2事件相互獨立，在P(A)=0或P(B)=0時滿足P(AB)=P(A)P(B) 也指A，B2事件相互獨立，即不可能事件與其他任何事件都相互獨立。

2)要注意區分相互獨立與兩兩獨立。若是2個事件兩兩獨立，實際上就是指相互獨立，但多于2個事件時則不同，以3事件為例，兩兩獨立只是指滿足P(AB)=P(A)P(B)，P(BC)=P(B)P(C)，P(AC)=P(A)P(C)，沒有了條件P(ABC)=P(A)P(B)P(C)也就不能叫相互獨立了。

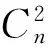
P(AiAj)=P(Ai)P(Aj) (i,j=1,2,…,n,且i≠j)

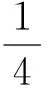
3)有一種理解是錯誤的：如果事件A與B是相互獨立的，則事件B發生(注：這里強調的是事件B發生，非事件B發生的概率)不受事件A發生與否的影響。

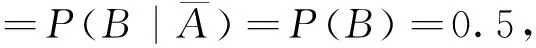
2 事件獨立性與互斥的關系

就獨立性與互斥而言，常常會被錯誤理解，認為二者都是一個發生與否與另一個不相干，2事件沒有關系也不能同時發生。互斥是指2隨機事件滿足A∩B=Φ。若A與B相互獨立且P(A)>0,P(B)>0，則P(AB)=P(A)P(B)>0，肯定不會有A∩B=Φ，即不但不能說明A∩B=Φ，恰恰能說明A∩B=Φ。當然了，如果A與B至少有一個是不可能事件，相互獨立仍然能夠說明互斥。

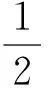
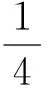
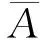
例4有2道單選題，記A1={第1道題答對}，A2={第2道題答對}，2事件是獨立事件，在2道題都不會的情況下亂猜答案，問只答對1道題的概率。

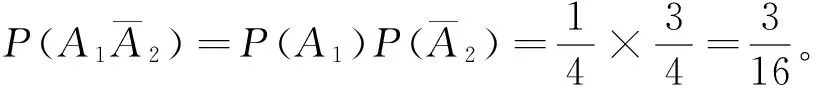
3 結合條件概率與幾何概率看獨立性

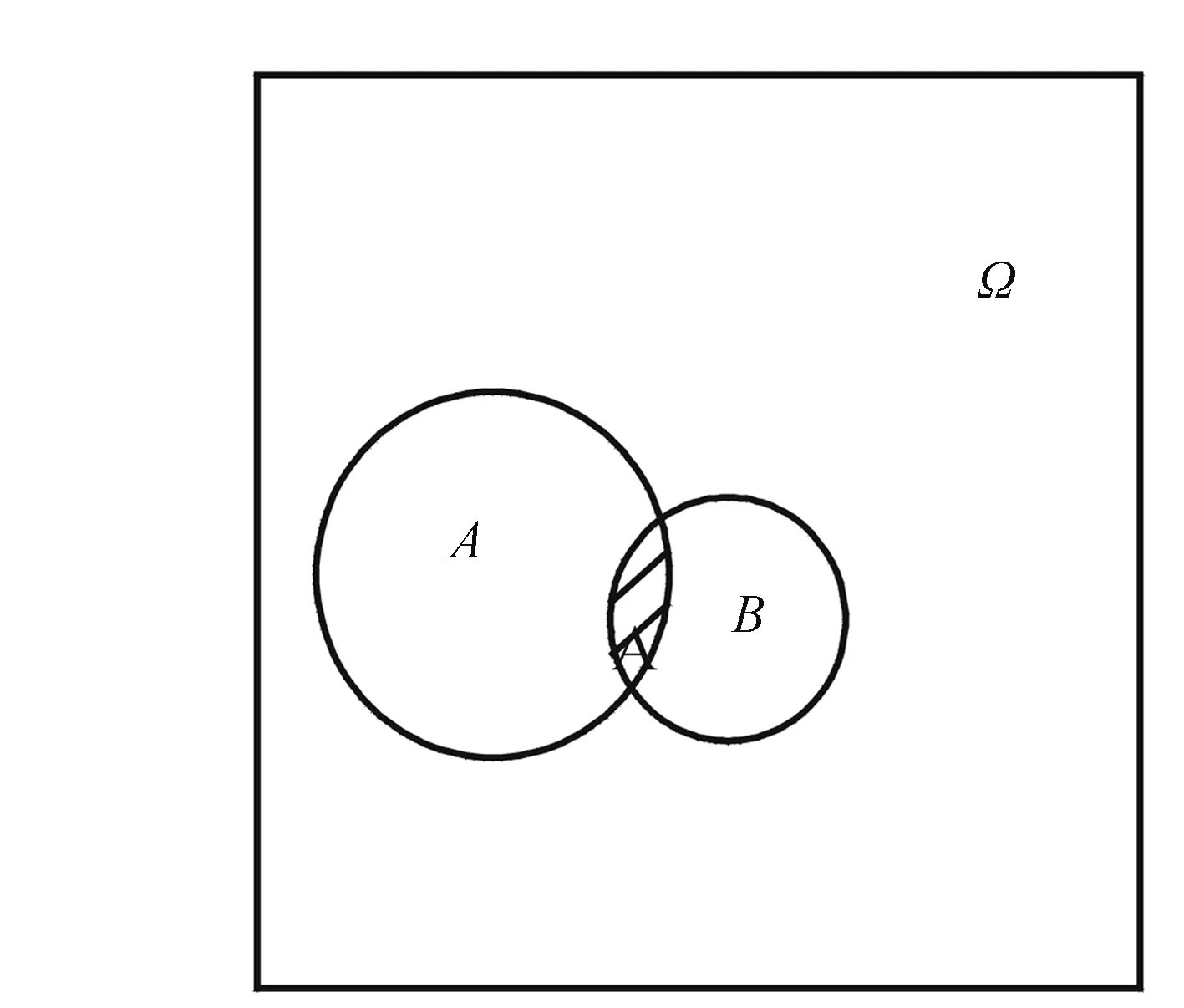
圖1 2事件獨立時反映的比例關系

如圖1:

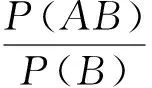
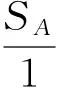
依條件概率知道，一般地，若計算A1，A2，…，An這n個事件同時發生的概率，需這樣計算：P(A1A2…An)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1)，所以計算起來相當繁瑣，每一個條件概率背后的實際意義可能會相當復雜，帶來的計算量也會非常大。如若能確保A1,A2,…,An這n個事件是相互獨立的，則只需利用P(A1A2…An)=P(A1)P(A2)P(A3)…P(An)來計算，大大減小了計算量，這也是為什么在很多時候做科學實驗時，要力求做到條件相同如同氣候、同溫度、同濕度、同高度等情況下重復試驗，以此來確保各事件的獨立性。

[1]龔德恩.經濟數學基礎(第3分冊)：概率統計[M].成都：四川人民出版社，2004.

[2] 鄭一，王玉敏，馮寶成.概率論與數理統計[M].北京：中國科學技術出版社，2007：33.

[3] 盛驟，謝式千，潘承毅.概率論與數理統計[M].北京：高等教育出版社，2009：20-21.

[4]張福利.隨機事件獨立性的教學探討[J].產業與科技論壇，2010，9(8)：212-213.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.10.047

O211

A

1673-1409(2011)10-0140-03