一類非線性廣義神經(jīng)傳播方程非協(xié)調(diào)元超收斂分析

郭志林 陸風(fēng)玲

(商丘師范學(xué)院數(shù)學(xué)系，中國 商丘 476000)

本文考慮下列變系數(shù)廣義神經(jīng)傳播方程

(1)

其中，X=(x,y)，Ω?R2為有界區(qū)域，?Ω為其光滑邊界，系數(shù)α(u)，β(X)滿足0<α0≤α(u)≤α1，0<β0≤β(X)≤β1，α0,α1,β0,β1為常數(shù)，且α(u),f(u),g(u)關(guān)于變量u滿足Lipschitz連續(xù)條件, 即

|ξ(u1)-ξ(u2)|≤Cξ|u1-u2|，u1,u2∈R,ξ=α,f,g,Cξ為正常數(shù)

(2)

且f(u),g(u)具有本文論證所需的二階有界偏導(dǎo)數(shù).

這一新型非線性發(fā)展方程，在神經(jīng)傳播過程中具有深刻的實際背景[1-3]，在生物、物理等領(lǐng)域有著廣泛的應(yīng)用，目前已有很多文獻(xiàn)對此方程進(jìn)行了研究[4-5].本文研究了方程(1)的非協(xié)調(diào)有限元在半離散格式下的收斂性.由于系數(shù)的非線性變化，相容誤差中的邊界估計若仍采用傳統(tǒng)的方法，將無法得到超逼近的結(jié)果，因此，通過引入平均值技巧，得到了相容誤差比插值誤差高一階的結(jié)果以及關(guān)于u在能量模意義下最優(yōu)的誤差估計和超逼近性質(zhì).最后，利用插值后處理技巧得到了半離散格式下整體超收斂結(jié)果.

1 單元的構(gòu)造

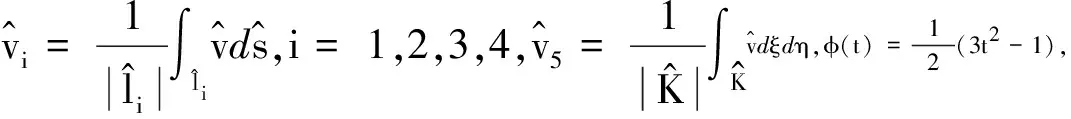
定義一般單元K上的函數(shù)v(x,y)如下：

相應(yīng)的有限元空間為

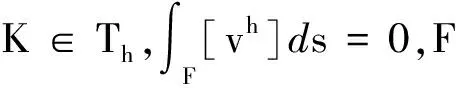
其中，[vh]表示vh跨過邊界F的跳躍度，當(dāng)F??Ω時，[vh]=vh.

2 各向異性網(wǎng)格下的半離散格式及收斂性分析

(3)

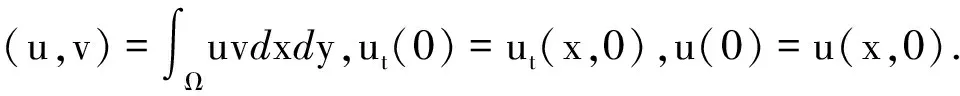
問題(1)的非協(xié)調(diào)有限元半離散格式為：求uh：[0,T]→Vh，使得

利用與[6]及[7]相同的方法可以證明, 當(dāng)t>0時，問題(4)的解是唯一存在的．

(▽(φ-Ihφ),▽v)h=0，

(5)

‖v‖0≤c‖v‖h，

(6)

(7)

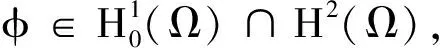
(8)

由上面的引理，我們得到

證令u-uh=(u-Ihu)+(Ihu-uh)=w+θ，其中θ∈Vh，?v∈Vh，由方程(1)和(3)得誤差方程

即

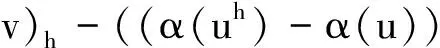
(9)

在(9)式中，令v=θt，兩邊對t從0到t積分，注意到θ(0)=θt(0)=0，有

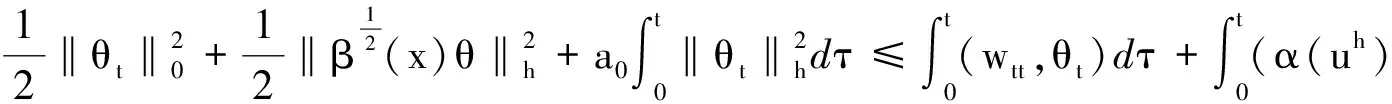
(10)

其中

由α(u)的有界性及ε-Young不等式

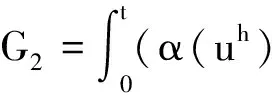
由α(u)的Lipschitz連續(xù)性及引理1可知

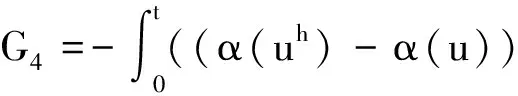
同理

由(7)式得

取適當(dāng)小的ε，整理得

由Gronwall不等式得

從而根據(jù)插值定理和引理2

定理1得證.

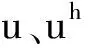
(11)

證G1，G4到G7用定理1的同樣證明方法.利用平均值技巧及α(u)的連續(xù)性，G2可以估計為

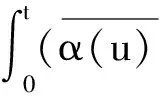
由(8)式得

同定理1，取適當(dāng)小的ε，整理并利用Gronwall不等式，即得(11).

利用文獻(xiàn)[10]的思想，構(gòu)造插值后處理算子I2h，完全類似于文獻(xiàn)[6]的證明，可以得到下面整體超收斂的結(jié)果：

注2對于(1)，這里我們只討論了β=β(X)的情形，而對于β=β(u)，目前還無法得到本文的收斂性結(jié)果以及整體超收斂的結(jié)論，這也是我們下一步主要研究的問題之一.

參考文獻(xiàn)：

[1] PAO C V. A mixed initial boundare value problem arising in neurophysicology [J]. J Math Anal Appl,1975,52(1):105-119.

[2] 程極濟,林克椿.生物物理學(xué)[M].北京:人民教育出版社,1982.

[3] 萬維明,劉亞成. 神經(jīng)傳播方程初邊值問題解的長時間行為[J].應(yīng)用數(shù)學(xué)學(xué)報, 1999,22(2): 311-315.

[4] 張志躍.一類廣義神經(jīng)傳播方程的有限元方法及數(shù)值分析[J].數(shù)學(xué)物理學(xué)報,2001,21(Z1):647-654.

[5] 王 波.一類神經(jīng)傳導(dǎo)方程的變網(wǎng)絡(luò)有限元方法及數(shù)值分析[J].生物數(shù)學(xué)學(xué)報,2006,1(1): 119-128.

[6] 石東洋,郝 穎. 廣義神經(jīng)傳播方程的一個各向異性非協(xié)調(diào)元超收斂分析[J].生物數(shù)學(xué)學(xué)報，2009,24(2): 279-286.

[7] 石東洋,張熠然.非定長Stokes問題的矩形型各向異性非協(xié)調(diào)元變網(wǎng)格方法[J].數(shù)學(xué)物理學(xué)報，2006,26A(5): 659-670.

[8] 明平兵.非協(xié)調(diào)元vs locking問題[D].北京：中國科學(xué)院計算數(shù)學(xué)研究院，1999.

[9] 胡俊.彈性力學(xué)問題的Locking-free[D].北京：中國科學(xué)院計算數(shù)學(xué)研究院，2004.

[10] CHEN S C, SHI D Y, ZHAO Y C.Anisotropic interpolation and qua-Wilson element for narrow qudrilateral meshes[J].IMA J Numerical Analysis,2004,24(1): 77-95.