小組合作學習在綜合實踐活動課上的運用
——“正方體涂色”教學實錄評析

●

(姜堰市第四中學 江蘇姜堰 225500)

小組合作學習在綜合實踐活動課上的運用
——“正方體涂色”教學實錄評析

●顏小兵

(姜堰市第四中學 江蘇姜堰 225500)

課題：正方體涂色

課型：活動課

活動目標：(1)通過正方體涂色分塊活動，使學生經歷從特殊到一般的認識過程，體會數學與生活的聯系；

(2)獲得研究問題的方法和經驗，加深對相關知識的理解；

(3)感受歸納的數學思維方法；

(4)培養學生的團結合作精神.

活動重點：探究研究問題的方法，譬如操作、分類、歸納、猜想、驗證等.

活動難點：正方體涂色問題中一般性規律的尋求.

活動方法：分組活動交流.

活動用具：正方體教具3個、多媒體課件，每小組準備小刀一把，表面涂色的正方體花泥3塊.

以下是本節課的教學實錄.

1 情境創設

師：今天是小明的生日，媽媽為她制作了一個大的正方體形狀的蛋糕，并把表面涂上了巧克力，小明決定和同學們一起分享，他把蛋糕切成了若干塊大小相同的小正方體分給同學們.那么每個同學所分到的蛋糕是否都涂有同樣多的巧克力呢？這節課我們就來做一個關于正方體的有趣活動——正方體涂色問題.

學生展開想象，各抒己見.

2 提出問題

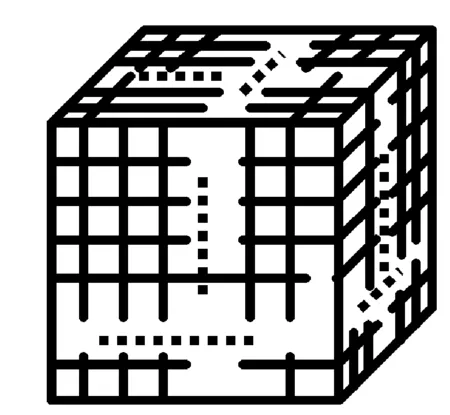
圖1

如圖1,把表面涂色的正方體的棱n等分，沿等分線把正方體切開，請問：

(1)能切出多少個小正方體？

(2)在這些小正方體中，它們的涂色情況有幾種？每種涂色情況各有多少個小正方體？

師：對于這樣一個復雜的、用字母表示的、有規律的問題，通常該怎么做呢？請同學們發表看法．

生1：可以從最簡單的情況開始考慮．

師：那么你認為最簡單的情況，題目中的n等于多少呢？

生2：n=2．

教師拿出棱二等分的表面涂色的正方體教具，向學生展示.

師：將這個正方體的棱二等分，沿著等分線把正方體切開，同學們想象一下，至少要切幾刀？

眾：3刀．

師：怎么切？

學生對這一問題非常感興趣，有一種新鮮感.按照公開課事前的合作小組的劃分，學生在指定的小組內積極討論，紛紛舉手發言，積極性很高，課堂氣氛開始活躍.

評注本教學環節利用學生生活中的事例，創設問題情境，激發求知的熱情和探索的欲望，讓學生經歷了將實際問題抽象為數學問題的建模過程.

3 提出活動要求

(1)使用活動工具要注意安全；

(2)活動時注意愛護公物(小刀不要切到課桌)；

(3)小組成員之間要團結協作.

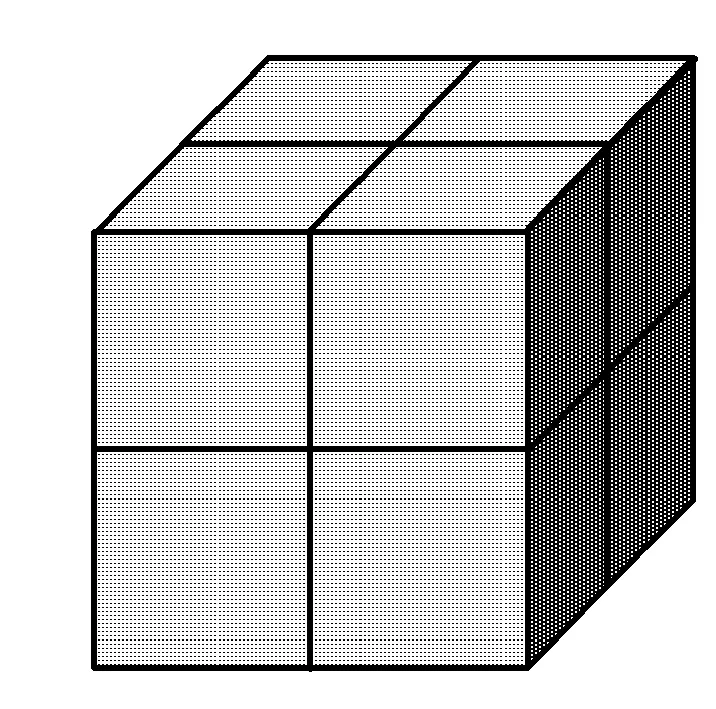
圖2

4 活動步驟

活動1把表面涂色的正方體的棱長2等分(如圖2)，然后沿等分線把正方體切開，得到幾個小正方體？觀察它們的涂色.

學生4人1組，每組取出一塊表面涂色的正方體花泥，推薦一人操刀，其他同學協助完成.教師不時地在一些小組中指點、討論、提問，學生小組討論、分類統計涂色情況，并填寫實驗表格(小組合作學習時間大約6分鐘).

全班交流各組動手操作的情況.

師：每個小組的活動都很認真，現在請各個小組匯報一下實驗結果．

生1：我們一共得到了8塊小正方體，每塊小正方體都有3面涂色．

生2：我們得到的結果跟他們一樣．

師：也就是說當n=2時，一共可以得到8塊小正方體，它們都是3面涂色．

師：剛才我們研究了二等分棱涂色情況，那么三等分棱的涂色情況又怎樣呢？

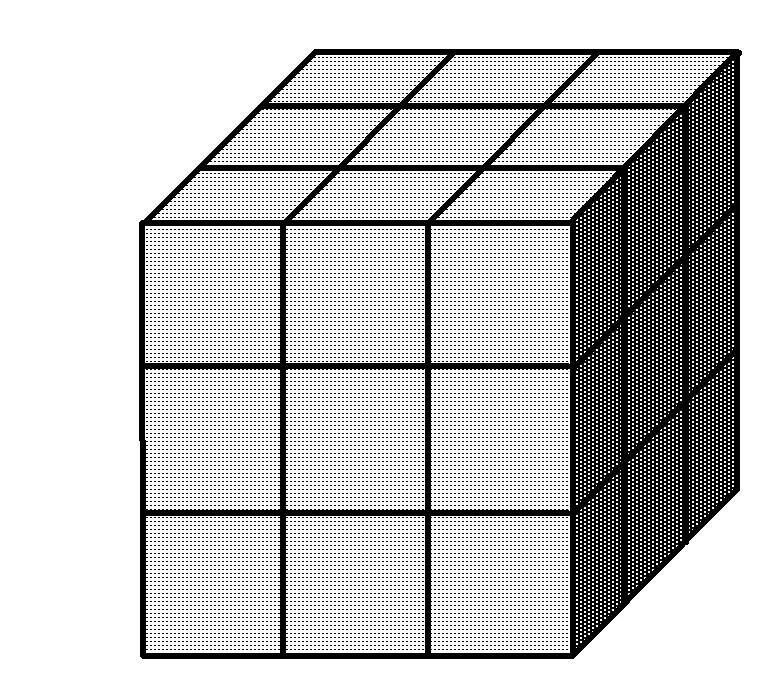
圖3

評注動手能使課堂更加生動活潑、更加主動和富有個性，憑著學生的動手操作，抓住正方體涂色的特征和涂色部分與正方體頂點、棱之間的關系，讓學生更加直觀地進行觀察、猜測、推理、交流.

活動2把正方體的棱長三等分，然后沿等分線把正方體切開，可得到幾個小正方體？觀察它們的涂色有幾種？每種涂色情況各有幾塊？

師：我們還是通過實驗來尋找問題的答案吧！接下來小組活動．

學生分組活動，4人分工合作，兩人一組配合，然后小組討論研究，接著將所切小正方體分類，有三面涂色的、有兩面涂色的……然后記錄員填寫實驗的數據(小組合作學習時間大約6分鐘).

師：每個小組的合作都很投入，現在請各個小組匯報實驗結果．

生1：一共得到27個小正方體，三面涂色的有8個、二面涂色的有12個、一面涂色的有6個、涂色的有1個．

生2：我們的實驗結果跟他們的是一樣的．

師：現在把切成的小正方塊，還原成一個大正方體．

教師的話還沒有說完，同學們便呼聲一片.

教師拿出切開后還原的模型(不完整)，請同學們繼續還原.

師：請仔細觀察每個模型的涂色情況，哪位同學愿意到前面試一下？

學生紛紛舉手，課堂氣氛再一次達到高潮，一名女同學到前面還原剩下的小正方塊模型.

師：我們先對這位同學的結果做個評價，成功嗎？

眾：成功．

師：請問這位同學，你是怎么知道這樣擺放的．

生3：它是有規律的．沒有涂色小方塊在正方體的中間，應該先填注．三面涂色的小方塊在角上．

師：同學們，應該在什么位置？

眾：頂點上．

師：一共有多少個？

眾：8個．

生3：二面涂色的在邊上，一條棱對應著一個.有12條棱，一面涂色的在每個面的中間，有6個．

師：非常棒！

評注這段極為精彩的師生對話顯示了教師與學生的配合非常融洽，說明了上課教師扎實的教學基本功和學生投入的聽課熱情.讓學生在充滿情感的、和諧的課堂氛圍中，在教師的鼓勵和引導中找到自信，體驗成功的樂趣．

師：大家已經知道了小正方體的涂色情況和它們的位置有關，剛才通過實驗知道了兩等分、三等分棱的情況，不做實驗能判斷涂色的結果嗎？請看活動3．

活動3如果把正方體的棱長四等分，你能猜出正方體被切成多少個小正方體嗎？觀察它們的涂色有幾種？每種涂色情況各有幾塊？

每個小組分別取出一塊表面涂色的正方體，推薦一人操刀，其他同學協助，分類、記數并填表，小組之間互相討論、交流小正方體表面的涂色情況(小組合作討論時間約8分鐘).

生1：如果等分棱數是4的話，那么總塊數就是64，三面涂色有8塊、二面涂色有24塊、一面涂色有24塊、無涂色的有8塊．

師：請問你是怎么分析的？

生1：要求總塊數的話，是用長乘以寬，再乘以高，就是4×4×4=64塊．

師：說的對.同學們也可以這樣看，每層有16塊，一共4層，共有64塊．

生1：三面涂色主要是看頂點，總共有8個；兩面涂色是看棱，每條棱上有2塊，共有12條棱，總共有24塊；一面涂色的是看面，一個面上有4塊，共有6個面，總共有24塊．沒有涂色的有8塊，在最中間．

師：怎么知道是8塊呢？

生1：我是用總塊數減去剛才所求的三面涂色、二面涂色、一面涂色的塊數．

師：很好.對于無涂色的8塊小正方體，除了用64減去三面、二面、一面所涂色塊數外，還有沒有其他的方法呢？

生2：還可以用(4-2)3.因為里面是2個單位的正方體，所以用(4-2)，得到它的長、寬、高.

師：很好，其實里面沒有涂色的部分仍然是一個正方體．

接下來，教師通過教具及多媒體演示進一步驗證了學生的猜想.

5 尋找規律

把正方體的棱長n等分，切成多少個等積小正方體？它們表面的涂色情況如何？

師：同學們，我們要研究n等分棱的情況，是否還要繼續研究五等分、六等分棱的情況呢？

生：不需要．

師：那么用字母表示的n等分棱的情況又是怎樣的呢？

各個小組進行了激烈地討論，互相幫助，小組討論、猜想，填寫猜想結果，說出猜想過程；驗證猜想結果，并安排小組代表上黑板填寫表11.

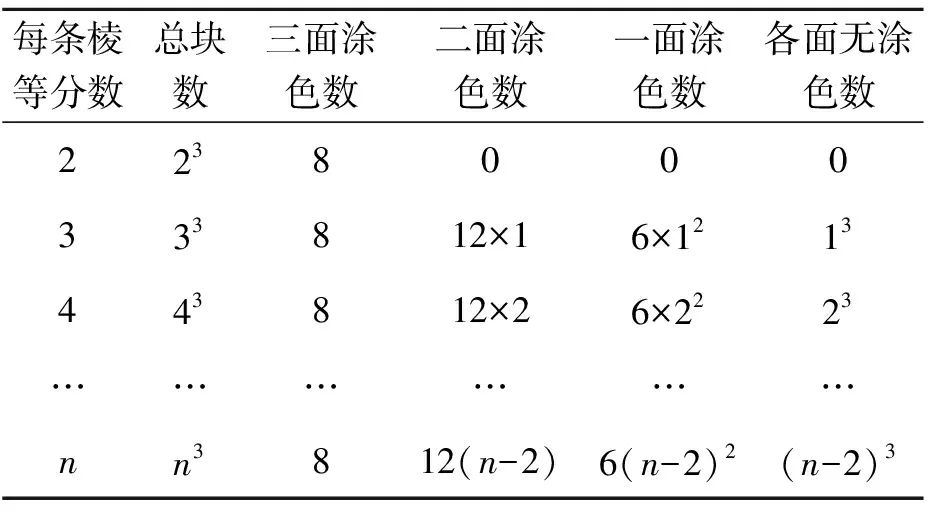
表1 小正方體表面涂色情況

(小組合作討論時間約5分鐘.)

師：看來大家討論有結果了，現在我們看剛才那位同學所填寫的，當n等分棱時，總塊數是n的三次方，這個結果對嗎?

眾：對．

生1：當棱數是n時，每一層是n2個，有n層，就是n的三次方．

師：說得非常好，三面涂色的小方塊仍然有8個，在哪兒呢?

眾：頂點上．

師：二面涂色的是12(n-2)，為什么呢？

生2：因為二面涂色的都在棱上，而一條棱上有2個頂點，所以要減去2個頂點就是(n-2)個，有12條棱，所以二面涂色的就有12(n-2)個．

師：說得太好了，一面涂色的呢？

生3：一面涂色的在面的中間，它也是一個正方形，它的邊長為(n-2).因為正方形有6個面，所以它的塊數就是6(n-2)2.

師：那么無涂色的呢？

生4：正方體的中間也是一個正方體，它的棱長就是(n-2).

師：是的，去掉涂色的以后，棱長就少了2，仍然是一個小正方體，因此無涂色的塊數就是(n-2)3.剛才大家都是從圖形的特征，發現了這些結果.我們在找邊的時候，還可以通過什么呢？

眾：數字.

師：對了，還可以通過數字的規律，譬如說總塊數8，27，64，它們都是些立方數，這樣n等分棱的總塊數就是n3.對于其他情況，也可以用這個方法考慮．

評注在這個活動中,教師不斷地引導、有梯度的提問，層層深入，同時讓學生在本組內充分交流.既給學生提供了表現的機會，又增強了學生的合作意識.當學生歸納總結時，教師還不斷地鼓勵、表揚和適當的補充、提升.

6 小結反思

談談你參與這次數學活動的感受，填寫數學活動評價表.

師：這節課我們通過學習二等分棱、三等分棱、四等分棱的特殊情況，研究了n等分棱的情況.其實生活中許多規律都是通過它的特殊情況進行研究的，請同學們回憶一下本節課的內容，談一談你的感受，或者說說有什么收獲．

生1：正方體的涂色情況與等分棱的棱數有關．

生2：不僅可以在圖形中尋找規律，而且在數字上也可以尋找規律．

生3：當解決一個復雜的問題時，可以先從簡單地、一般地問題找出規律，以此類推到復雜的問題．

生4：我懂得了實踐操作中可以解決許多問題．

生5：我知道了團結的力量．

評注這樣的暢談收獲很自然.學生由數學知識的學習過程聯想到數學思想方法，聯想到生活的哲理，顯示了這堂課的成功亮點，讓學生真正體會到學數學的快樂.

7 課后活動

1.如果把長、寬、高分別是5 cm、4 cm、3 cm的長方體切成棱長為1 cm的正方體，小正方體表面的涂色情況怎樣？

2.當長方體的長、寬、高分別為acm、bcm、ccm時，小正方體表面的涂色情況怎樣？

課例總評本節綜合實踐活動，教師始終以開展活動為主線，在課堂上通過小組合作學習的形式、動手操作的方式進行教學.教師不斷加大問題的難度，有梯度地慢慢引入，符合學生的認知水平，調動了學生探索的積極性.本節課采用了獨立思考、交流探討、啟發教學的模式，同時以開放的問題為載體，通過學生的動手實踐，讓學生真正動起來、說起來、想起來.在得出問題的結果時,不是單憑教師直接把結果“塞”給學生，而是恰到好處地激發、引導、探討，讓學生真正理解問題解決的來龍去脈與前因后果，讓學生主動參與活動、參與研究，體現了“教師為主導、學生為主體、探究為主線、思維為核心”的教學思想，培養了學生良好的學習習慣和思維品質.