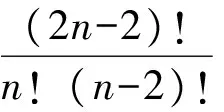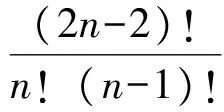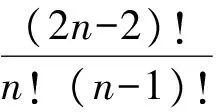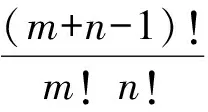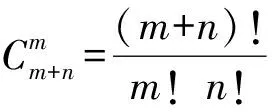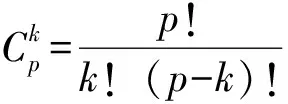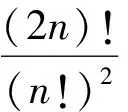一道IMO試題的證明及其推廣

●(深圳中學 廣東深圳 518001)●(廣州大學附屬中學 廣東廣州 510050)

一道IMO試題的證明及其推廣

●周峻民(深圳中學 廣東深圳 518001)●鄭慧娟(廣州大學附屬中學 廣東廣州 510050)

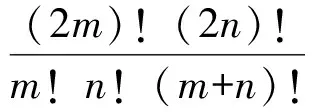
(第14屆IMO試題)

該試題是第14屆國際數學奧林匹克(IMO)競賽的第3題,簡記為IMO.14.3.它的背景是2個數論函數的應用:方次數函數potpn和下取整函數?x」．

1 知識背景

方次數函數potpn：表示素數p在正整數n的素因數分解中的次數(若素數p不是n的素因數,則次數記為0)．如20=22·5，則pot220=2，pot320=0，pot520=1．

下取整函數?x」：表示不超過實數x的最大整數(即x的整數部分)．如?1.2」=1，?3」=3．

這2個數論函數在數論中非常有用，由定義可得到下列簡單的性質：

性質1potp(mn)=potpm+potpn.

性質2b/a是整數的充要條件是：對任意素數p，有potpb-potpa≥0．

性質3?x」+?y」≤?x+y」≤?x」+?y」+1.

性質4當n是整數時，?n+x」=n+?x」．

將這2個數論函數聯系到一起，得到以下性質：

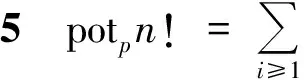
2 試題的證明

證明由性質1知

potp(2m)!(2n)!=potp(2m)!+potp(2n)!,

potpm!n!(m+n)!=potpm!+potpn!+potp(m+n)!.

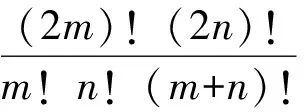
[potp(2m)!+potp(2n)!]-[potpm!+potpn!+potp(m+n)!]≥0.

由性質5，該問題可轉化為證明：對任意素數p，

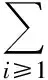
到這一步，思路有點卡住了，因為這5個“無限求和”是大問題．能否把這5個“無限求和”合并呢？合并之后，如果每一項的值非負，那么它們的和也是非負的.于是，希望得到：對任意素數p和任意正整數i，必有

(1)

由于式(1)中素數p是任意的，正整數i也是任意的，因此更一般地，如果可以做到：對任意實數x,y，必有

(2)

那么問題就迎刃而解了．

式(2)中x,y是任意實數，范圍有點大，下面嘗試把x,y的范圍變小．設x=?x」+a，y=?y」+b，其中a,b∈[0,1)．由性質4知

?2x」=2?x」+2?a」，?2y」=2?y」+?2b」，?x+y」=?x」+?y」+?a+b」，

代入可得

?2x」+?2y」-?x」-?y」-?x+y」=

(2?x」+?2a」)+(2?y」+?2b」)-?x」-?y」-(?x」+?y」+?a+b」) =?2a」+?2b」-?a+b」,

再次簡化得：對任意實數a,b∈[0,1)，必有

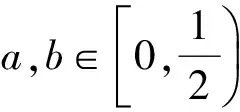
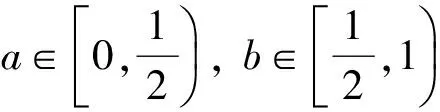
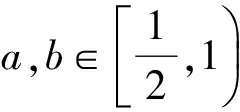
綜上所述，對任意實數a,b∈[0,1)，式(3)恒成立，命題得證．

3 試題的推廣

由試題的證明過程可知，IMO.14.3的背景就是式(2)，而式(2)又可簡化為式(3)，由此可編制出相同背景的試題．

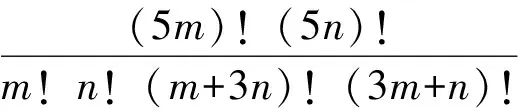
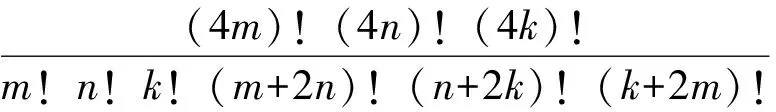
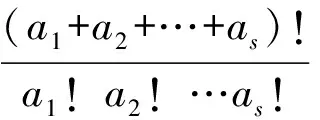
上面3個推廣和IMO.14.3“形狀”相似，解法也相似，留給感興趣的讀者．

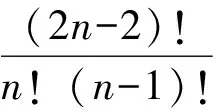
乍一看，推廣4與IMO.14.3“形狀”相似，但是仔細觀察可發現2n-2

對任意實數x，必有

?2x-2」≥?x」+?x-2」,?2x-2」≥?x-1」+?x-1」.

類似于IMO.14.3的證明方法，可得P，Q是整數．

推廣5～7與推廣4的證法類似.下面2個推廣與推廣4的證法不一樣，留給感興趣的讀者．

推廣9證明：m!n!整除(mn)!．

[1] 柯召，孫琦.數論講義[M].北京：高等教育出版社，2001.

[2] 潘承洞，潘承彪.初等數論[M].北京：北京大學出版社，2003.

[3] 柳柏濂，吳康.競賽數學的原理和方法[M].廣州：廣東高等教育出版社，2003.