改進的國際工程項目投資風險模糊評價

劉進，高軒能

（華僑大學 土木工程學院，福建 泉州 362021）

改進的國際工程項目投資風險模糊評價

劉進，高軒能

（華僑大學 土木工程學院，福建 泉州 362021）

首先在全面分析國際工程項目投資風險影響因素的基礎上，建立合理的國際工程項目投資風險評價指標體系；其次，針對使用層次分析法確定的固定權重存在較大主觀性的缺陷，引入激勵與懲罰并舉的局部變權原理對固定權重進行調整，提出使用變權層次分析法和熵權法相結合的方法確定綜合權重，進而提出改進的國際工程項目投資風險模糊綜合評價模型；最后，通過實例分析與計算，驗證該模型的有效性和合理性.

投資風險評價；國際工程項目；評價指標體系；變權層次分析法；熵權法；模糊評價

國際工程項目具有投資大、周期長、復雜性、風險較大等特點，業主稍有不慎就可能造成重大損失，因此，如何有效地對國際工程項目的投資風險進行評估就成為了重要的研究內容.目前的層次分析法在確定固定權重時存在較大的主觀性，大多按照專家的知識和經驗來確定，容易使結果與實際情況產生偏差 .本文引入局部變權原理對固定權重進行調整，提出改進的國際工程項目投資風險模糊綜合評價模型，并建立了國際工程項目投資風險評價指標體系.

1 模型的建立

1.1 建立國際工程項目投資風險評價指標體系

國際工程項目的投資風險復雜多樣.文中以大量的實際調查資料為基礎，廣泛收集有關專家學者的經驗，經過綜合歸納、分析、研究和對比后，將國際工程項目的投資風險分為以下6個大類.

（1）政治風險，主要是指由戰爭、國際局勢、政權更迭和政策變化帶來的風險 .如東道國的政局、外交關系和項目所在地區的社會穩定、行政審批，以及東道國有意或無意變更政策等不確定因素可能給業主造成的損失［1］.

（2）經濟風險，主要指國家或社會一些經濟政策或其他因素的不確定性變化所帶來的風險［2］.如東道國的匯率、利率、通貨膨脹及資金流動的管制政策和業主的融資能力等，都是影響投資的重要因素.

（3）自然風險，主要指工程項目所在地的地理、地質、水文和氣象等自然環境因素，以及洪水、地震、火災、臺風、雷電等不可抗拒自然力因素帶來的不可預測的風險.

（4）管理風險，主要指由合同訂立的嚴謹程度、承包商的履約情況、材料和設備供應商的履約情況、監理工程師是否盡職，以及工程質量是否達標等不確定因素帶來的風險［3］.

（5）設計風險，主要指由設計帶來的風險，包括設計方聲譽、技術成熟度和勘測準確性等3方面.工程設計是工程質量的根本，如果設計上出現失誤，輕則返工修復，重則可能導致工程毀損，給業主造成重大損失.

（6）技術風險，主要指業主經驗和管理能力不足帶來的風險［4］.國際工程項目的風險龐雜多樣，因此對業主的決策能力、經驗和項目管理水平都是嚴峻的考驗.

將上述國際工程項目的各種風險因素層層分解，構建出國際工程項目投資風險評價指標體系，如表1所示.表1中：國際工程項目投資風險稱為總風險，下一個層次的風險稱為A級風險，即政治風險、經濟風險 、自然風險、管理風險、設計風險、技術風險，它顯示了風險的來源，A級風險之下的風險稱為B級風險，即最低層次的風險，是指具體的風險因素.

表1 國際工程項目投資風險評價指標體系Tab.1 Investment risk index system of international engineering project

1.2 建立評語集

由于風險分析的需要，將評語集劃分為“很大、大、中、小、很小”5個級別.評語集一般用大寫字母Y表示，即Y＝｛很大，大，中，小，很小｝，對其賦值為｛90，70，50，30，10｝.

1.3 建立評價矩陣

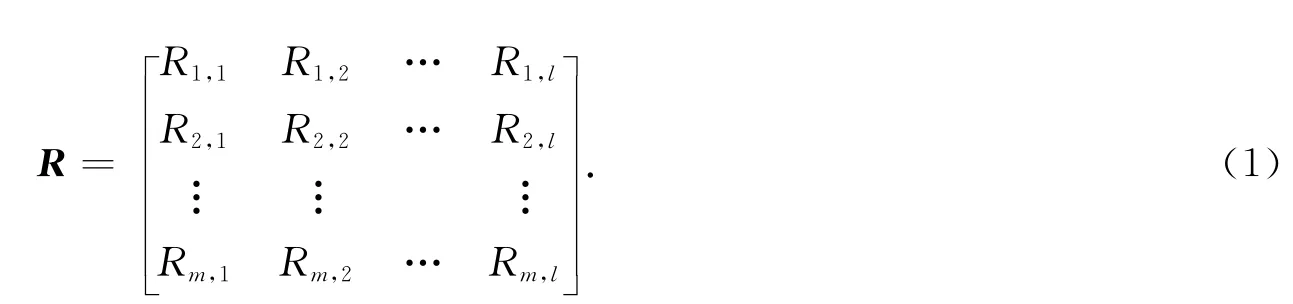
式（1）中：Ri，j（i＝1，2，…，m；j＝1，2，…，l）為第i個評價指標對于第j個評價等級的隸屬度，它反映了評價指標與評價等級之間用隸屬度表示的模糊關系［5］；m表示評價指標的數目；l表示評語集中評價等級的數目.

1.4 變權層次分析法確定權重

層次分析法是一種把定性和定量分析相結合的系統分析方法，在風險評價中經常使用.其基本步驟［6］：（1）建立遞階層次結構，將有關的各個評價指標按照不同屬性自上而下分解成若干層次，形成遞階層次結構；（2）構造兩兩比較的判斷矩陣，在建立了遞階層次結構以后，對同一層次的各評價指標關于上一層次中某一準則的重要性進行兩兩比較，根據評定尺度確定其相對重要程度，構造兩兩比較判斷矩陣；（3）由判斷矩陣計算被比較評價指標對于該準則的權重并作一致性檢驗；（4）組合一致性檢驗.

用層次分析法確定的指標權重是固定的，不會因狀態或評價指標的不同而改變；但實際上，人們對客觀事物進行評價時所運用的并不是固定權重［7－8］.變權重的根本思想在于引入激勵懲罰機制，即某個風險項的評價值較低時，說明該項風險較小，則給予一定的激勵，增加其權重，使整體風險評價值降低；反之，當某個風險項的評價值較高時，表明該項風險較大，則給予一定的懲罰，增加其權重，使整體風險評價值升高，從而使整體風險評價值更趨科學、合理.

根據局部變權的公理化定義，設評價指標的固定權重為a0i，局部狀態變權向量為Sj（x），則變權向量a′i（x）可表示為

局部狀態變權向量Sj（x）的定義為

因此，當0≤xj＜0.3時，懲罰程度最大；當0.3≤xj＜0.5時，懲罰程度隨著xj的減小而增大；而當0.5≤xj＜0.85時，既不懲罰也不激勵；當0.85≤xj≤1時，激勵程度隨xj的增大而增大.

經過以上步驟，得到變權重集A′＝｛a′1，a′2，…，a′n｝.其中：n為某個B 級風險評價指標的個數.

1.5 熵權法確定權重

熵權法是一種客觀賦權方法，其原理是根據各指標數值的變異程度所反映的信息量大小來確定權重.設有h個評價指標，k個評價對象，由它們形成的原始數據矩陣W′＝（w′i，j）h×k，則熵權值的計算步驟［9］：（1）對W′各個指標值的數據歸一化處理，得到矩陣W＝（wi，j）h×k；然后，計算第i項指標下第j 個評價對象指標值w權重，即有

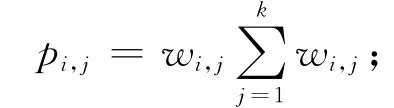
（2）計算第i項指標的熵值

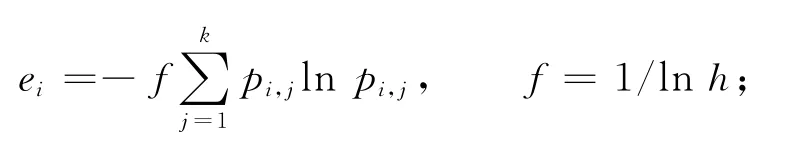
（3）計算指標i的差異性因數gi＝1－ei；（4）確定指標i的熵權值

1.6 綜合權重的確定

變權層次分析法在確定權重時，雖然考慮了專家的知識和經驗，并且引入了局部變權原理計算變權重，使權重的確定具有較高的合理性和科學性，但仍然存在主觀隨意性的缺陷.熵可以度量評價指標體系中指標數據所蘊含的信息量，并依此確定各指標的權重，結果較為客觀，但是這種客觀權值有時與實際情況相差較大.綜合分析這兩種方法的優勢和劣勢，文章把變權層次分析法和熵權法相結合，得到綜合考慮主客觀評價指標的權重向量a＝（ai）1×n，即

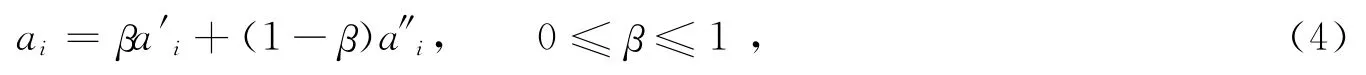
組合權重隨β的改變而改變，當β＝1和β＝0時，分別對應于變權層次分析法和熵權法.關于β如何合理取值有很多討論，通過比較各指標的重要程度等級、變權層次分析法所得權重和熵權法所得權重的3種排序可知，β分別取0，0.5和1.0.文中根據國際工程項目的具體情況，取β＝0.5.

1.7 模糊綜合評價

運用模糊運算法則［10－11］，進行綜合運算，有

式中：A為評價指標的權重集；R為評價矩陣.先進行一級模糊綜合評價，得出一級模糊綜合評價的結果Bi＝Ai×Ri；然后，進行二級模糊綜合評價，由R＝［B1，B2，…，Bi，…，Bm］T組成二級評價矩陣，m 為A級風險的個數，得到總評價向量B＝A×R；最后，使用加權平均法處理，得出綜合評價結果.

2 應用實例

2.1 確定一級評價矩陣

由多位專家對B級風險評價指標的風險程度進行評價，組成一級評價矩陣，如表2所示.

表2 一級評價矩陣列表Tab.2 One－level evaluation matrix

2.2 權重的確定

2.2.1 變權重 使用專家調查法和層次分析法來確定固定權重 .根據評價矩陣和風險等級量化集計算風險評價指標的綜合評分，由綜合評分所對應的區間得到Sj（x），再確定變權重.各級風險變權重的確定，如表3所示.

2.2.2 熵權重 由上述熵權法的計算式計算各級評價指標的熵權重，結果如表3所示.

2.2.3 綜合權重 根據式（4），計算各級評價指標的綜合權重，結果如表3所示.

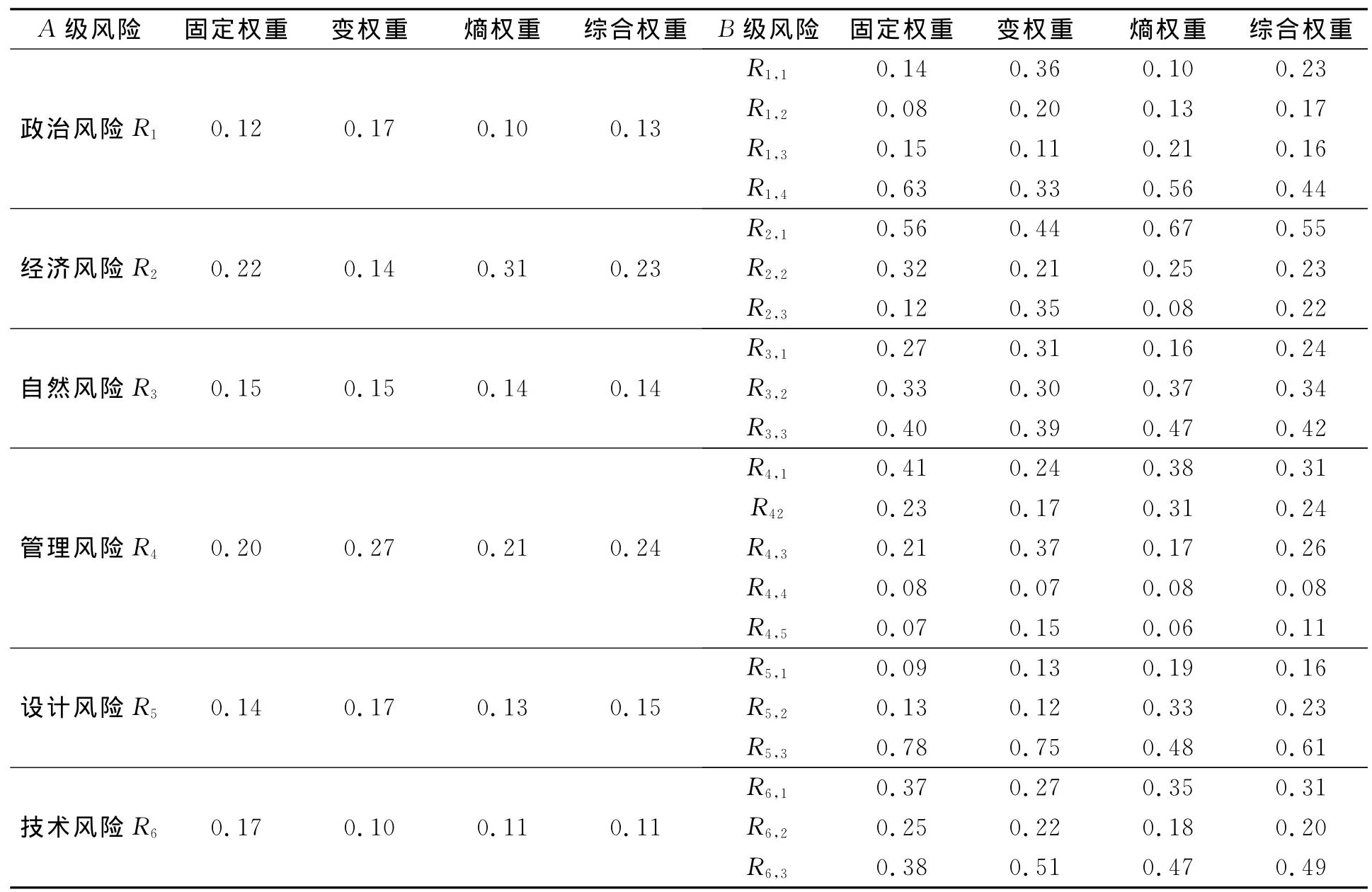
表3 投資風險評價指標的權重確定Tab.3 Weight determination of investment risk index

2.3 模糊綜合評價

根據式（5）進行一級模糊綜合評價，有

同理可得

然后，進行二級模糊綜合評價，有

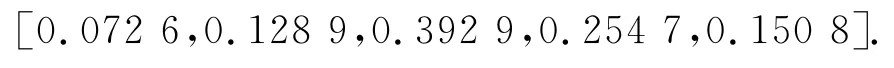
對結果做加權平均處理，有0.072 6×90＋0.128 9×70＋0.392 9×50＋0.254 7×30＋0.150 8×10＝44.351，最終得出該國際工程項目投資風險的綜合評分為44.351，風險等級屬于中等偏小.

3 結束語

文中引入局部變權原理計算變權重，實現對某些風險評價指標的獎勵和懲罰.采用變權層次分析法和熵權法相結合的方法確定綜合權重，將主觀判斷與客觀計算相結合，使得權重的確定更加科學、合理，從而確保了評價結果的可靠性.建立全面合理的國際工程項目投資風險評價指標體系，提出基于變權層次分析法和熵權法的二級模糊綜合評價模型，為業主提供了重要的參考和依據.

［1］陳偉珂.工程項目風險管理［M］.北京：人民交通出版社，2008.

［2］陳勇，吳靜.國際工程風險管理［J］.資源環境與工程，2010，24（4）：2－3.

［3］章凌云，黃奕輝，張云波.工程質量管理及工程質量保證擔保［J］.華僑大學學報：自然科學版，2005，26（3）：275－278.

［4］劉爾烈.國際工程管理概論［M］.天津：天津大學出版社，2003.

［5］羅云，樊運曉，馬曉春.風險分析與安全評價［M］.北京：化學工業出版社，2004.

［6］王艷紅，王秀麗.國際工程風險模糊綜合評價［J］.山西建筑，2007，33（31）：2－3.

［7］熊蘭，劉鈺，林蔭宇，等.模糊變權法在絕緣子狀態綜合評判中的應用［J］.電力系統及其自動化學報，2010，22（1）：2－3.

［8］李彥鵬，黎湘，王宏強，等.應用變權模糊綜合評判的目標識別效果評估［J］.現代雷達，2010，26（12）：1－2.

［9］陳亞哲，劉桂珍，劉挺，等.基于熵權的產品廣義質量模糊綜合評價［J］.東北大學學報：自然科學版，2010，31（2）：2－3.

［10］楊倫標.模糊數學原理及應用［M］.廣州：華南理工大學出版社，2002.

［11］郭玉翠，王勵成，鈕心忻.一個用于多個實體信任度評估的模糊數學模型［J］.華僑大學學報：自然科學版，2009，30（6）：637－641.

Improved Fuzzy Evaluation of Investment Risk in International Engineering Project

LIU Jin，GAO Xuan－neng

（College of Civil Engineering，Huaqiao University，Quanzhou 362021，China）

Based on a comprehensive analysis of the factors affecting investment risk in international engineering project，the investment risk evaluation index system was established.Since there exist subjective shortcomings in the fixed weight determined by analytic hierarchy，the local variable weight principle combining penalty with incentive was introduced to adjust the fixed weight.The synthetic weight was determined by the conbination of analytic hierarchy process based on variable weight and entropy weight method.A model based on improved fuzzy synthetic evaluation was put forword.A case study was presented to verify the feasibility and rationality of the model.

investment risk evaluation；international engineering project；risk evaluation index system；analytic hierarchy process based on variable weight；entropy weight method；fuzzy evaluation

TU 72；F 284

A

1000－5013（2011）06－0689－05

2011－04－15

高軒能（1962－），男，教授，主要從事工程結構理論與項目管理的研究.E－mail：gaoxn1962＠163.com.

中央高校基本科研課題資助項目（JB－JC1005）

（責任編輯：黃曉楠 英文審校：方德平）