滲透數學模型 優化“問題解決”

　　“問題解決”是小學數學教學的主要教學目標之一。“問題解決”教學可以培養學生分析問題、探究問題、解決問題的能力。數學模型是用數學語言對所研究的系統所作的一種數學抽象，它摒棄了一切非本質的屬性，刻畫出該系統中一些主要因素的關系和特征。應用數學模型方法可以對實際問題的研究提供決策依據和預測，還能為解決實際問題提供優化的方案。
　　一、滲透數學模型，培養分析問題的能力
　　分析問題是解決問題的起點，也是解決問題的基礎。如果分析問題不正確，那么正確地解決問題就成為空中樓閣。教學中，為了能使學生在分析問題中得到解決問題的最佳方法，教師可以通過建立數學模型，對各種方案進行數學分析，并從中挑選出最合理的方案。
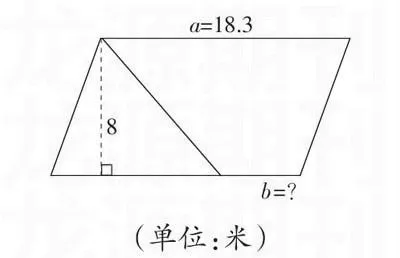
　　例如，有這樣一道題：“王大伯有一塊平行四邊形的地（如下圖），他準備把這一塊地分成三角形和梯形兩部分，分別用來種青菜和蘿卜。梯形和長方形的面積相差32平方米，他準備在b處開一扇籬笆門，那么這一扇籬笆門的長度應該是多少米？”
　　對于這道題，教師可以引導學生利用數學建模的思想進行分析問題。首先，引導學生在理解圖意的基礎上分析數量關系，并用數學語言建立數學模型：①b＝a－三角形底邊的長度，于是要算出三角形底邊的長度，而三角形底邊的長度＝三角形的面積×2÷8；②b=梯形的面積÷4－a；③ b=兩個圖形的面積之差÷8。再分別對這三個數學模型代入數據進行計算比較，使學生體會到：運用①②兩個數學模型計算，不但計算步驟多，而且其中三角形的面積和梯形的面積都不知道，還需要計算；而利用模型③計算，其中的兩個條件都是已知的，并且只需一步計算，可見模型③是解決本題的最優方案。像上例中，引導學生利用數學模型多角度地分析問題，可以有效培養學生的發散思維能力和思維的敏捷性，從而獲得最優化的問題解決方案。
　　二、滲透數學模型，培養探究問題的能力
　　小學數學知識按知識wc6tcweCdoG3wfbHm3JfPA==形式大致可分為概念性知識、規律性知識和技能性知識，如各種運算定律和求面積、周長的公式屬于規律性知識。實際上，在這些規律性知識的結論中，往往涉及一個簡單的數學模型。所以，在教學這些規律性知識時，教師要引導學生自己去探索發現數學模型，也就是讓學生自己表述問題，分析實際問題中的本質關系，用數學符號把這種關系表達出來，并分析自己所建立的數學模型是否合理，在此基礎上再進行計算，解決實際問題。
　　例如，教學“乘法結合律”一課，教師可以給學生出示幾組算式，先要求學生口算，然后把得數相等的算式用等號連起來。接著讓學生觀察和驗證下列等式——（6×20）×5＝6×（20×5）、（13×8）×125＝13×（8×125），分析其中關系，然后引導學生自己舉例，并用字母把這一關系表達出來，即（a×b）×c＝a×（b×c）。最后通過解決實際問題使學生懂得這一結論不只限于一道或幾道具體題目，而且a、b、c可以代表任意數，從而使這個數學模型得以推廣運用。上述過程，實際上就引導學生參與了發現數學知識的過程。學生自己去探索、去分析其中的數量關系，用數學語言把這種關系表達出來，從而培養了學生主動探究問題的能力，以及運用數學語言進行概括的能力。
　　三、滲透數學模型，培養解決問題的能力
　　數學認知過程，都是從實際問題開始，經過觀察、比較、分析、綜合、抽象，概括出數學理論知識，再運用到實際中去解決問題。教師在“問題解決”教學中滲透數學模型方法，可以培養和提高學生解決實際問題的能力。
　　l．在典型問題教學中滲透數學模型方法
　　例如，在教學行程問題、價格問題等典型問題時，可先讓學生分析數量關系，并用數學語言表達，如路程＝速度×時間、總價＝單價×數量等。然后讓學生通過計算充分理解數學模型中各個字母所表示的普遍含義，更清楚地掌握題中的數量關系，發展學生的抽象概括能力。
　　2．在一般問題教學中滲透數學模型方法
　　教學中要側重分析量與量之間的本質聯系。問題解決列式計算的過程，實際上就是對原始資料進行數學抽象，并建立數學模型的過程。首先，要引導學生分析數量關系，分析各種變量之間的關系，并突出其中的主要關系。其次，引導學生進行數學抽象，培養學生運用數學符號表述的能力。再次，可以對算式進行優化。這些都是建立數學模型的特點。
　　3．在列方程解應用題中滲透數學模型方法，要側重建立含有未知數的數學模型
　　在列方程解應用題中，列方程也就是建立一個含有未知數的數學模型，其關鍵是要找到一個含未知數的等量關系，并用數學符號表示出來。
　　總之，在問題解決教學中滲透數學模型方法，有利于幫助學生理解數量關系，提高學生分析問題、探究問題和解決實際問題的能力。
　　（責編藍天）