二維Tsallis熵閾值法中基于粒子群優化的參數選取

林愛英， 李 輝， 吳莉莉， 昝紅英

(1.河南農業大學 理學院 河南 鄭州 450002；2.鄭州大學 信息工程學院 河南 鄭州 450001)

0 引言

閾值分割因其簡單有效而成為廣泛使用的圖像分割方法，人們對此進行了大量研究[1-3].基于熵概念的閾值選取方法,因其良好的信息論背景頗受關注，其中由Kapur 等[4]較早提出的一維最大Shannon熵閾值法因分割效果較好且實現簡單，而成為最具代表性的方法.其后人們基于廣義信息論相繼提出了Renyi熵[5]、Tsallis熵[6-7]等多種熵閾值分割算法，并推導出相應的二維算法[8-9]，國內也有許多學者對熵閾值分割算法進行了相關的研究[10-11].

通常把Renyi熵和Tsallis熵稱為廣義信息熵，其信息熵中含有參數，參數的特殊取值可以得到經典的Shannon熵，參數的合理取值可以獲得比最大Shannon熵閾值法更好的分割性能，但至今其參數的選取沒有一個準則.針對Renyi熵，Sahoo等[8]指出對大部分圖像而言，參數q取0.7是一個比較合適的參數值，而對于Tsallis熵，Sahoo等[9]指出，參數q取0.8時能得到較好的分割結果.考慮到實際應用中圖像的復雜性，用一個固定的參數值來選取閾值有其局限性，文獻[12]給出了一維Renyi熵閾值分割法的一種參數自適應選取思路.考慮到在二維灰度直方圖上進行閾值選取，能夠利用圖像的更多信息，因此主要研究二維Tsallis熵閾值分割方法中參數q的自適應選擇問題.

基于均勻性測度作為分割圖像質量評價準則，作者利用粒子群優化搜索方法，提出了一種二維Tsallis熵閾值法中參數q的選取方法.實驗表明，本文方法可以根據不同的圖像自適應的選取參數q，獲得較好的圖像分割效果.

1 二維Tsallis熵閾值法

對于一幅大小為M×N的數字圖像F，用f(x,y)表示圖像上坐標為(x,y)的像素點的灰度值，f(x,y)∈G={0,1,…,L-1}，定義坐標為(x,y)的像素點的K×K鄰域的平均灰度值g(x,y)為

(1)

其中,[]表示取整運算,K為鄰域寬度，一般取奇數,則g(x,y)∈G={0,1,…,L-1}.

如果用r(i,j)表示相對應的灰度值(f=i)-鄰域灰度值(g=j)對出現的頻次(0≤r(i,j)≤M·N)，定義p(i,j)是灰度級-鄰域灰度級對出現的概率

(2)

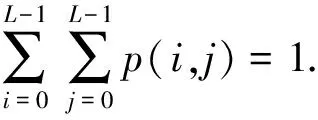
圖1 二維直方圖區域劃分示意圖

根據二維直方圖的定義，在閾值(s,t)處將圖像分割成如圖1所示的4個區域.其中，對角線上的兩個區域1和2分別對應于目標和背景，遠離對角線的區域3和4對應于邊緣和噪聲.一般認為在區域3和4上所有的p(i,j)≈0.

由圖1可知，利用二維直方圖中任意閾值矢量(s,t)對圖像進行分割，可將圖像分成目標和背景兩類區域，分別記為C0和C1，則這兩類的先驗概率分別為：

(3)

(4)

滿足P0(s,t)+P1(s,t)≈1.

(5)

(6)

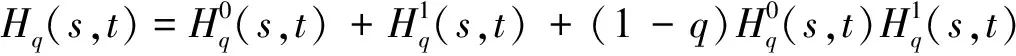
(s*,t*)=arg max[Hq(s,t)],0≤s,t≤L-1.

(7)

分割后二值圖像fT(x,y)的取值為

(8)

一般的，b0取0，b1取255.

如何選取式(7)中的參數q是二維Tsallis熵閾值分割方法的難點，至今尚無明確的解決方案.文獻[12]給出了一維Renyi熵閾值分割法的一種參數自適應選取方法，作者受此啟發主要研究二維Tsallis熵方法中參數q的自適應選擇問題.理論上講，參數q的取值范圍在(0,+∞)，為了獲得最優的q值，這里采用粒子群算優化法(particle swarm optimization,PSO)對其進行優化搜索.

2 基于PSO的自適應參數選取

2.1 PSO優化算法

PSO算法最早由Eberhart 等[13]提出，是一種基于鳥類覓食的隨機群體搜索過程.設在n維解空間中，有N個粒子組成一個群落，第i個粒子的位置為Xi=(xi1,xi2,…,xin)，“飛翔”速度為Vi=(vi1,vi2,…,vin).前者表示問題的解，將Xi帶入一個目標函數,可以計算出其適應值，根據適應值的大小衡量Xi的優劣；后者表示粒子從當前位置移動到下一個位置的速度大小.求解時首先對粒子群的位置和速度進行初始化，然后通過迭代方式在解空間中尋找最優解.假設第i個粒子迄今為止搜索到的最優位置為Pi=(Pi1,Pi2,…,Pin)，稱為個體最優極值，整個粒子群迄今為止搜索到的最優位置為G=(g1,g2,…,gn)，稱為全局極值.基本PSO采用式(9),(10)對粒子操作[14]

Vi=ω·Vi+c1·r1·(Pi-Xi)+c2·r2·(G-Xi),

(9)

Xi=Xi+Vi,

(10)

其中，慣性因子ω是非負數；學習因子c1和c2是非負常數；r1和r2是介于(0,1)之間的隨機數.迭代中止條件根據具體問題一般選為最大迭代次數或粒子群迄今為止搜索到的最優位置滿足預定最小適應閾值.基本PSO算法需要用戶確定的參數少、操作簡單，使用比較方便，但是它容易陷入局部極小點.研究者們提出了自適應調整的策略，即隨著迭代的進行，線性地減小ω的值.作者采用這種改進的自適應PSO算法來進行優化搜索.

2.2 自適應PSO參數選取

在文獻[8]中指出，Renyi熵的參數q在(0,1)之間，并建議q取經驗值0.7，不能隨著圖像的不同而改變，這在一定程度上就失去了參數熵的優勢.在文獻[9]中分析了參數q對Tsallis熵閾值分割的影響，但沒有給出參數q的選取方法.根據文獻[12]，作者通過PSO優化搜索算法對參數q在其取值空間進行全局尋優，以均勻性測度函數UM作為適應度函數對q閾值進行評價，自適應地找出最優的參數q及相應的分割閾值.

均勻性測度是用來評價分割方法性能的一個指標.一個區域內的均勻性與區域內的方差成反比，區域均勻性越好，其灰度分布越集中.均勻性測度可計算為[15]

(11)

其中，Ri表示分割后的第i個區域，i=1,2，Ai表示區域Ri中的像素總個數，C是歸一化參數.最優的q取值為

q*=arg max[UM(t(q))],q>0.

(12)

以式(12)作為PSO算法的適應度函數，可以根據不同的圖像，在q的變化空間內自適應地搜索參數q的取值，從而進一步確定圖像的分割閾值.對于Tsallis熵而言，參數的維數為1.一般的，粒子的個數根據實際應用不同進行選取，選取N=10個粒子來進行搜索，參數空間取(0,1)可以滿足要求[7].自適應PSO搜索參數的具體步驟如下.

步驟1：粒子群初始化 對于PSO算法需要確定的參數有：

①粒子的初始位置X及初始速度V：由于每一個粒子代表一組參數，第i個粒子的初始位置為xi，在(0,1)區間隨機選取粒子的初始位置.初始速度可以從初始位置中得到，這里選vi=rand(0,1).一般的，為了避免粒子飛行過快，飛過全局最優值，需要設定粒子的最大速度.粒子速度變化范圍為[-Vmax,Vmax]，Vmax=0.15.

②學習因子c1和c2：取c1=2.8，c2=1.3.

③慣性因子ω：慣性因子對PSO算法的性能有很大的影響，采用自適應調整慣性因子的方法來控制PSO的整體搜索效率.初始慣性因子選為1.0，隨著迭代次數的增加，慣性因子線性地減小，如式(13)所示，

ω(t+1)=ωmax-(ωmax-ωmin)·t/iter,

(13)

其中，ωmax和ωmin分別為權重的最大和最小值.一般的，ωmax=0.95，ωmin=0.4，iter為迭代次數，取iter= 30.

步驟2： 計算每個粒子的適應度值 對于第i個粒子，首先利用(7)式計算二維Tsallis熵(q=xi)，選取圖像最佳閾值；然后利用(12)式計算對應第i個粒子的適應度值.重復上述過程計算所有粒子的適應度值.

步驟3： 對于每個粒子，將其適應值與所經歷過的最好位置的適應值進行比較，如果更好，則將其作為粒子的個體歷史最優值，用當前位置更新個體歷史最好位置.

步驟4： 對每個粒子，比較它的適應度值和群體所經歷的最好位置的適應度值，如果更好，更新最好位置.

步驟5： 根據(9)和(10)式調整粒子的速度和位置.

步驟6： 如果達到結束條件(足夠好的位置或最大迭代次數)，則結束，否則轉步驟2.

3 結果與分析

利用上述提出的自適應PSO參數選取方法，對二維Tsallis熵閾值法中的參數進行選取，通過對大量不同類型的灰度圖像進行的閾值分割實驗發現，相對于參數q取固定值的分割方法[9](q取0.8)，自適應PSO參數選取方法的分割結果更為準確，目標和背景邊緣及噪聲點的錯分大為減少.現給出其中4幅圖像兩種算法分割的實驗結果(圖2～圖5)，相應的分割閾值及參數q的取值列于表1.

圖2 cameraman圖像及分割結果

圖3 moon圖像及分割結果

圖4 航拍圖像及分割結果

圖5 rose圖像及分割結果

表1 兩種方法的分割閾值及參數q取值比較

從圖2(c)，圖3(c),圖4(c),圖5(c)可以看出，基于PSO優化的自適應參數選取法能使分割后的圖像區域的內部均勻、邊界形狀更準確、細節特征更清晰.這是因為本文的分割方法基于圖像分割評價準則—均勻度測試準則，致使目標和背景邊緣及噪聲點的錯分大為減少的緣故；從圖2(b)～圖4(b)可以看出，固定參數選取的分割方法已經不能有效地把目標和背景分割開來，出現了大量的錯分點；從圖5可以看出，盡管兩種方法都能取得比較好的分割結果，但本文的方法在目標和背景邊緣處分割效果更好.由表1可以看出，參數q在(0,1)區間變化時，確實可以取得最佳的分割閾值.

4 結論

作者針對二維Tsallis熵閾值法中參數q的選取問題，以圖像分割效果評價準則—均勻度測試準則為適應性函數，利用PSO 優化搜索算法，在q的變化空間內進行優化搜索，根據具體的圖像自適應地選取參數q，從而得到合適的分割閾值，這種方式更適合圖像分割問題的要求.在實際工程應用中，遇到的圖像比較復雜，如果對所有圖像都使用相同的參數q，必然是不合適的.因此，從理論上來看，結合圖像本身的信息，自適應的選取參數的方法可以更好地發揮參數熵的優勢，本文的實驗結果也驗證了這一觀點.

[1] Lee S U,Chung S Y.A comparative performance study of several global thresholding techniques for segmentation[J].Computer Vision,Graphics and Image Processing,1990,52(2): 171-190.

[2] Shaoo P K,Soltani S,Wong A K C.A survey of thresholding techniques[J].Computer Vision,Graphics and Image Processing,1988,41(2): 233-260.

[3] 閆成新,孫亮.圖像過渡區直接提取與分割快速算法[J].鄭州大學學報:理學版,2006,38(4): 74-77.

[4] Kapur N,Sahoo P K,Wong A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision,Graphics,and Image Processing,1985,29(3):273-285.

[5] Sahoo P K,Wilkins C,Yeage J.Threshold selection using Renyi’s entropy[J].Pattern Recognition,1997,30(1): 71-84.

[6] Tsallis C.Nonextensive physics: a possible connection between generalized statistical mechanics and quantum group[J].Physics Lett A,1994,195(5/6):329-334.

[7] Portes de Albuquerque M,Esquef I A,Gesualdi Mello A R.Image thresholding using Tsallis entropy[J].Pattern Recognition Letters,2004,25(9):1059-1065.

[8] Sahoo P K,Arora G.A thresholding method based on two-dimensional Renyi’s entropy[J].Pattern Recognition,2004,37(16):1149-1161.

[9] Sahoo P K,Arora G.Image thresholding using two-dimensional Tsallis-Havrda-Charvat entropy[J].Pattern Recognition Letters,2006,27(6): 520-528.

[10] 吳一全,潘喆.二維Tsallis-Havard-Charvat熵值分割的快速遞推算法[J].信號處理,2009,25(4): 665-668.

[11] 張毅軍,吳雪菁,夏良正.二維圖像閾值分割的快速遞推算法[J].模式識別與人工智能,1997,10(3):259-264.

[12] 雷博,范九倫.一維Renyi 熵閾值法中參數的自適應選取[J].光子學報,2009,38(9): 2439-2442.

[13] Eberhart R C,Kermedy J.A new optimizer using particles swarm theory[C]//Proceedings of Sixth International Symposium on Micro Machine and Human Science.Nagoya,1995: 39-43.

[14] Eberhart R C,Shi Y H.Tracking and optimizing dynamic systems with particle swarms[C]//Proceedings of the Congress on Evolutionary Computation.Seoul,2001: 94-100.

[15] 章毓晉.圖像分割評價技術分類和比較[J].中國圖象圖形學報,1996,1(2): 151-158.