天然藥物提取過程的傳質動力學模型

王伯初，蘇輝，楊憲，劉瑋琦，錢俊臻，李偉

(重慶大學生物工程學院生物流變科學與技術國家教育部重點實驗室，重慶400044)

天然藥物是一個含有許多未知組分的復雜體系［1-2］。天然藥物的有效組分大多存在于植物細胞內，提取的實質是溶質從藥材內部擴散到外部溶劑的傳質過程［3］。天然藥物提取過程分為五步［3］:①溶劑流動及向藥材表面的擴散;②溶劑向天然藥物內部的滲透;③藥材內部溶質的溶解;④溶質從藥材內部向表面的擴散;⑤目標組分向外部溶劑的擴散。其中①和⑤稱為外擴散，②和④為內擴散，③實質上為溶質的溶劑化過程。內擴散為溶劑提取的控制步驟［3-4］。因此，天然藥物的提取是一個復雜的傳質過程，需要研究影響溶質轉移的關鍵因素及內部機制，以改善天然藥物提取工藝。

在天然藥物的工業化生產中，提取工藝參數的設置仍然以經驗為主，普遍存在提取效率低的現象，迫切需要相應的理論指導。Spiro等［5-6］研究紅茶中萃取茶黃素和咖啡因，從Fick第一定律出發建立了溶質擴散的動力學方程。田君等［7］和Carola等［8］以土茯苓為例，用實驗數據擬合控制模型和M-M方程，根據擬合度來選擇合適的模型;林亞平等［9］基于Fick第一定律，通過對擴散系數和濃度梯度的定量假設，建立了非溶蝕性藥物體系的釋放動力學模型。該模型中假設擴散系數是濃度的函數，濃度梯度是時間的函數。隨后，儲茂泉等［10-11］假設擴散系數和濃度梯度都是溫度的函數，建立了中草藥浸提過程的動力學模型，可描述浸出有效成分濃度與浸提時間，溶劑倍量、顆粒粒度、浸提溫度的函數關系。李有潤等［12］和Hou［13］基于傳質定律，考慮有效成分的高溫分解與揮發，以當歸芍藥散的提取過程為例建立了中藥提取優化模型。賀福元等［14］根據傳質定律、Noyes-Whitney溶出理論建立了不同體系下中藥提取過程的方程組，運用拉式變換求解，提取過程的速率常數由強度性工藝參數和容量性工藝參數決定。

現有的數學模型只考慮了有效成分濃度與外界條件(溫度，濃度，顆粒半徑，溶劑體積等)的關系，而沒研究有效成分提取率的變化。本實驗考慮高溫分解及吸附作用，建立了更具有普遍意義的動力學模型，并用綠原酸的提取實驗對該模型進行檢驗。

1 天然藥物有效成分提取的數學模型

采用溶劑法從天然藥物中提取有效成分，這個過程是溶解傳質過程，可以作如下假設:

1)擴散假設:提取過程完全由有效成分向顆粒表面的內擴散控制，不考慮表面向溶劑的外擴散，另外溶質的擴散為一維擴散;

2)形狀假設:藥材顆粒為多孔球形;

3)濃度分布:顆粒在溶劑的存在是均勻的，即外部的提取液為均勻場。

1.1 天然藥物提取基本模型假定藥材為多孔球形顆粒，半徑為R，提取液體積為Vl，根據Fick擴散第二定律［16］，有:

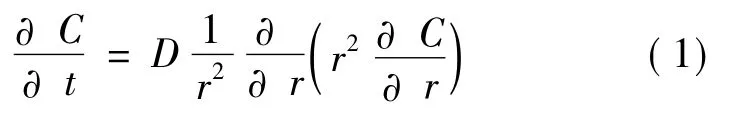
初始條件及邊界條件如下:

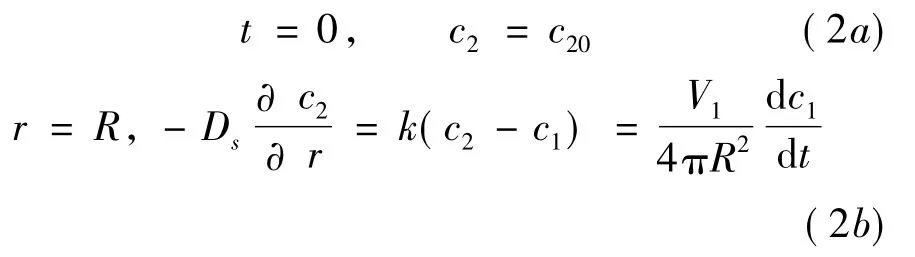
式中k表示對流傳質系數。積分，求解可得:

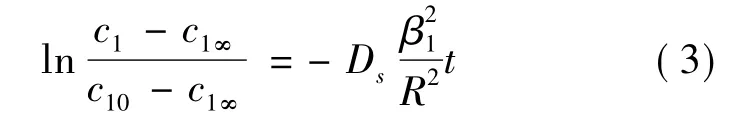
其中β1為超越方程βctgβ=1－的第一個根;c1為外部溶劑中的有效成分的濃度，c10是外部溶劑的有效成分的初始濃度。式(3)為天然藥物提取的一級動力學方程。

1.2 模型的改進根據現有的研究成果，天然藥物提取過程的動力學服從如下一級動力學方程［15-16］:

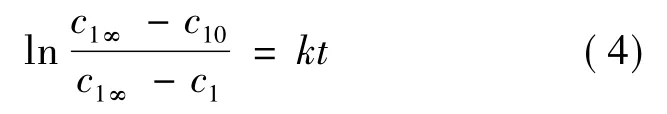
由Fick第二定律推導可得:

考慮到有效成分在高溫下的分解，有效成分既有擴散到主體溶液中，又被分解成其它物質。根據質量守恒:

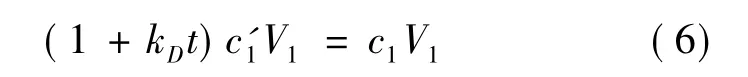
以(1+kD t)c'1代替c1，代入(3)可得提取率為:

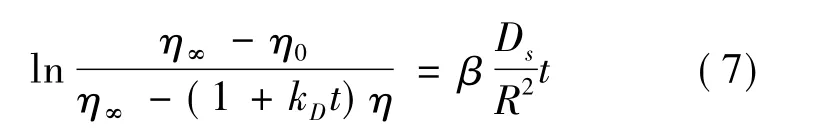
溶解平衡和吸附平衡決定了溶劑提取所能達到的極限。吸附主要是基于固體表面對鄰近溶質分子的親和作用，吸附作用的大小與吸附表面積和溫度有關，表面積大、溫度低有利于吸附，高溫有利于脫附［4，17］。

在不考慮高溫分解的情況下，無窮時刻顆粒內外濃度相等。吸附作用導致殘留在顆粒表面的有效成分含量為ma，吸附質量與表面積成正比，與提取溫度成反比［17］，根據Gibbs吸附公式可得［17］:

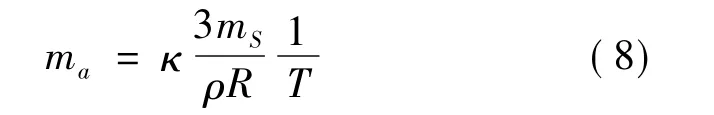
在不存在分解作用的前提下，無窮時刻有效成分的濃度為:

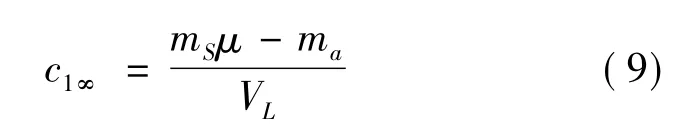
根據提取率的定義，無窮時刻提取率可表示為:

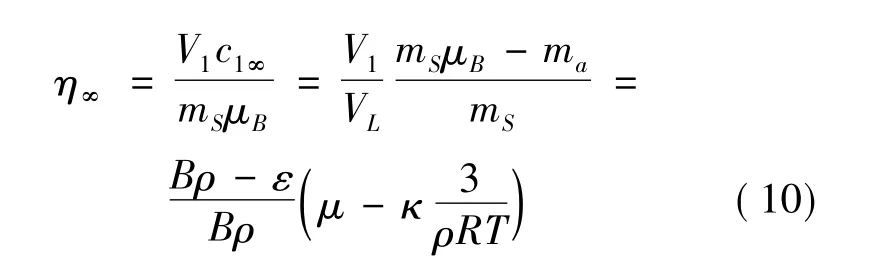
式中:B=(V1+V2)/mS，B為溶劑倍量，mS=ρ*VS，ρ為藥材密度，ε為孔隙率，V2為內部溶劑的體積，kD為擴散系數，修正后的模型考慮了高溫的分解，藥材的密度以及孔隙率等因素，得到了無窮時刻的提取率與相關參數的關系式。

2 模型參數計算

2.1 擴散系數對溶質為較小分子的稀溶液，擴散系數Ds可以用威爾蓋公式計算［12-13］:

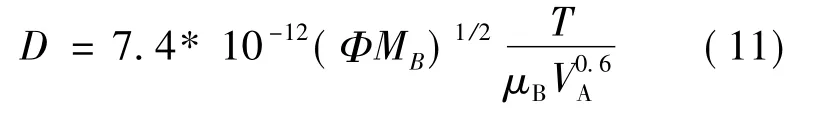
其中:Φ為溶劑的締合參數，T為絕對溫度，MB為溶劑的分子量［18］，VA為溶質的分子體積，μB為溶液黏度。依據擴散系數的公式，可知擴散系數與溫度(T)成正比，與溶質的分子體積(VA)和溶液黏度(μB)成反比。

2.2 初始濃度以及提取率初始時經過洗滌過程，有效成分從顆粒表面迅速溶解到溶劑中。根據儲茂泉等［10-11］的研究成果并加以改進，初始濃度可表達為溫度、顆粒半徑和溶劑倍量的函數:

初始時刻提取率為:

式(13)給出了初始時刻的提取率與外部溶劑中溶質的初始濃度的關系，還與藥材的本身屬性(溶液黏度μB，ρ為藥材密度)有關。

3 實驗

3.1 原料、試劑與主要儀器金銀花(重慶康迪藥業有限公司)，綠原酸對照品(中國藥品生物制品檢定所，批號110753-200413)，無水乙醇(AR級)，乙腈(色譜純)，磷酸(分析純)，高效液相色譜儀(島津2010AHT)，DF-101S集熱式恒溫加熱磁力攪拌器(河南鞏義市予華儀器有限責任公司)，FA2004電子分析天平(上海恒平科學儀器有限公司)。

3.2 標準曲線本實驗采用HPLC對綠原酸定量。精密稱取綠原酸對照品2.96 mg，用50 mL乙醇溶解，搖勻，作為原液。吸取原液10 mL，用純水稀釋至50 mL作為對照品溶液。精密吸取對照品溶液1.0、2.0、3.0、4.0、5.0、6.0、7.0 mL，分別置于10 mL棕色量瓶中，用純水稀釋至刻度，搖勻。以綠原酸質量濃度(μg/mL)為橫坐標，峰面積為縱坐標作圖，通過制作標準曲線。綠原酸質量分數測定的回歸方程為:y=1 783.4x－18 000，R=0.999 5，線性關系良好，線性范圍:12.4～180 μg/mL。

3.3 試驗方法綠原酸的提取過程在常壓下采用攪拌回流在恒溫加熱磁力攪拌器中進行。實驗條件為:乙醇為70%，溶劑倍量為10 mL/g，攪拌速度為50 r/min，溫度分別為T1=40℃、T2=50℃、T3=60℃、T4=70℃、T5=80℃，金銀花粒度分別為20目、40目、60目、80目。實驗研究溫度與提取率的關系，金銀花的粒度為40目;金銀花粒度與提取率的關系，溫度為T3=60℃。

4 結果與討論

4.1 擴散系數由式(12)可以計算得到不同操作條件下的有效擴散系數，表1給出了不同黏度，溫度，溶劑締合參數下的擴散系數的值，可知擴散系數在10－9～10－10m2/s的范圍內［12］。表1說明了溫度越高，溶劑的締合參數、擴散系數越大;而溶液黏度越大，擴散系數越小。溫度升高，擴散系數會增大，這是由于溫度升高時，分子會加快運動，加快有效物質的擴散速度，從而使擴散系數增大。而溶液黏度越大，藥材顆粒運動的阻力變大，擴散速度變小，從而使擴散系數變小。

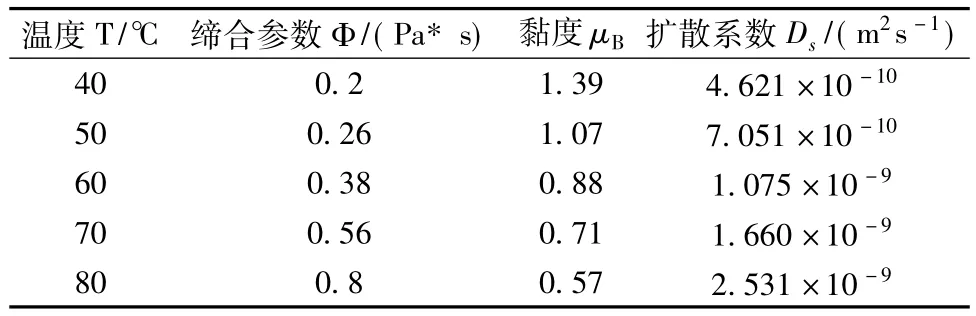
表1 不同條件下的擴散系數Tab.1 Diffusion coefficients under different conditions

4.2 模型驗證通過建立的動力學模型，對不同條件下的提取過程進行驗證，所得的計算值與試驗值的擬和情況見圖1和圖2。從金銀花中提取綠原酸的實驗，分別考慮了不同提取溫度和顆粒粒度條件下測得浸提過程的動力學數據。

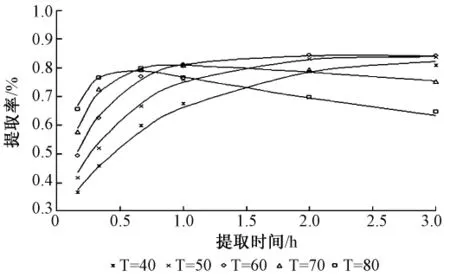
圖1 不同溫度(℃)下的提取率與提取時間的關系Fig.1 Relation of extraction efficiency to extraction time at different temperature(℃)

從表1可知，70%的乙醇，不同溫度下的提取率隨時間變化的實驗值和理論值的擬合度很好。隨著溫度的升高，綠原酸的提取率逐漸增大，當溫度為60℃時綠原酸提取率達到最大，為80.98%。因為溫度升高有助于藥材的組分的溶解，同時也會促進溶質的擴散速度。但是溫度超過60℃，綠原酸提取率反而下降。溫度的升高也有利于藥材表面溶質的脫附，同時高溫會促進綠原酸的分解，從而使得提取率下降，60℃為最佳的提取溫度。

從圖2可知，金銀花粒度40目時，綠原酸提取率最高。當金銀花的粒度低于或高于40目時，提取率均呈現下降的趨勢。隨著藥材粒度值變大(20～40目)，單位質量的藥材的總比表面積越大，促進溶劑的滲透及綠原酸的提取速度越快，有利于提高提取率。但金銀花粒度過大(40～80目)，會使藥材的總比表面積過大，吸附作用也會增強，使得提取率下降。同時，粉碎過細使得細胞破裂，使得不易溶出的樹脂進入溶液中，黏度增大，擴散速度降低，最適采用粒度為40目的金銀花來提取綠原酸。

5 結論

在現有模型的基礎上，根據Fick第二定律，以內擴散為主，考慮了高溫的分解以及吸附作用，得到具有普遍的動力學模型，并對模型進行了求解，得到了初始濃度和提取率的表達式。改進后的模型反映了天然藥物有效成分的提取率與浸提時間、提取溫度和藥材粒度之間的關系。金銀花提取綠原酸的試驗值與理論值吻合情況良好，改進后的模型能很好的說明提取率與外界參數(溫度和金銀花粒度)的關系，為今后天然藥物提取有效成分的工藝提供理論依據。

［1］Shao L，Yi L Z，Liang Y Z.Traditional Chinese medicine and separation science［J］.J Separat Sci，2008，31:2113-2137.

［2］Deng C H，Yao N，Zhang X M，et al.Development of microwave-assisted extraction followed by headspace single-drop micro extraction for fast determination of phenols in traditional Chinese medicines［J］.J Chromatogr A，2006，1103:15-21.

［3］馮年平，郁威.天然藥物提取分離技術原理與應用［M］.北京:中國醫藥科技出版社，2005.

［4］蘇輝，王伯初，劉瑋琦，等.天然藥物提取過程的動力學數學模型［J］.中草藥，2011，42(2):1-8.

［5］Spiro M，Selwood R M.Kinetics and mechanism of caffeine infusion from coffee:The effect of particle size［J］.J Sci Food Agric，1984，35:915-924.

［6］Spiro M，Jaganyi D.Kinetics and equilibria of tea infusion，Part 15.Transport of call eine across a teabag membrane in a modified rotating diffusion cell［J］.Food Chemistry，2000，69:119-124.

［7］田君，池汝安，高洪，等.乙醇提取土茯苓黃酮甙的動力學研究［J］.天然產物研究與開發，2005，17(1):11-15.

［8］Carola T，Gerhard G，Markus P，et al.Mathematical treatment of transport data of bacterial transport systems to estimate limitation in diffusion through the outer membrane［J］.J Theoretical Biol，2000，207:1-14.

［9］林亞平，盧維倫.非溶蝕型藥物體系的釋放動力學新模型——Fick第一擴散定律的修正及其應用［J］.藥學學報，1997，32(11):869-873.

［10］儲茂泉，古宏晨，劉國杰.中草藥浸提過程的動力學模型［J］.中草藥，2000，31(7):504-506.

［11］儲茂泉，古宏晨，劉國杰.中草藥浸提溫度對有效成分浸出濃度的影響［J］.中草藥，2001，32(1):22-23.

［12］李有潤，鄭清.中草藥提取過程的數學擬合與優化［J］.中草藥，1997，28(7):399-411.

［13］Hou K F，Zheng Q，Li Y R，et al.Modeling and optimization of herb leaching processes［J］.Comp Chem Eng，2000，24:1343-1348.

［14］賀福元，鄧凱文，羅杰英，等.中藥復方成分提取動力學數學模型的建立及參數分析［J］.中國中藥雜志，2007，32(6):490-495.

［15］儲茂泉，劉國杰.中藥提取過程的動力學［J］.藥學學報，2002，37(7):559-562.

［16］歐陽平，張高勇，康保安，等.苦葉七中類黃酮提取的動力學及相關熱力學研究［J］.中成藥，2004，26(12):991-995.

［17］趙振國.吸附作用應用原理［M］.北京:化學工業出版社，2005.

［18］解祥夫，趙貴哲，劉亞青.PR方程對固體溶質的模擬計算［J］.應用化學，2006，35(12):978-984.