用并聯補償解耦法設計MIMO控制的仿真
黃 威,夏 洪,張秀喜,堯 征,鄭振峰
(東華理工大學 機械與電子工程學院,江西 撫州 330013)
1 引言
各個控制通道中的耦合廣泛存在于多輸入多輸出(MIMO)的系統當中,并且時滯現象往往會影響單輸入對單輸出(SISO)的穩定性和控制的特性。對于實際成產過程當中,往往多個變量相互關聯,一個輸出受多個輸入的控制,一個輸入控制多個輸出,并且各個控制通道存在不同程度的滯后,這樣解耦補償矩陣成為了解決滯后現象的關鍵。傳統解決這一問題的方法主要有:前饋補償解耦、反饋補償解耦、對角矩陣解耦,但是對角矩陣補償法(Diagonal Matrix Decoupling method,DMD)是廣泛應用的解耦方法。但從一些資料上看來,在用這種方法計算耦合項的函數項時,都把延時項去掉,這樣大大簡化計算的復雜性。而在實際的工程應用過程中,如果將延時項去掉的話,控制的穩定性和系統的特性將大大縮小。
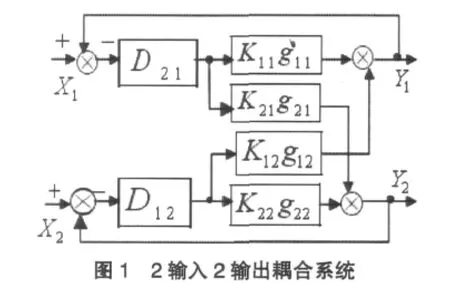
假設有圖1所示的2輸入2輸出耦合系統,X1通K21g21過對X2管道有耦合作用,表達式為:
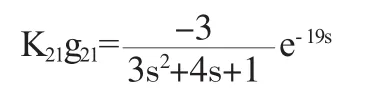
X2通過對X1產生耦合作用其表達式為:
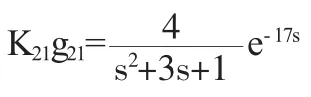
X1通道的被控制量的表達式為:
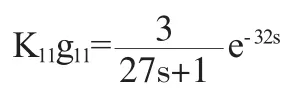
X2通道的被控制量的表達式為:
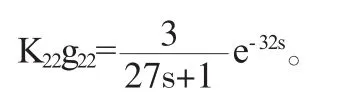
X1,R(s),K和Y1共同構成通道,通常采用預估器和解耦器,控制器為回路的控制圖,如圖 2 所示,R(s),Y(s)表示系統輸入,輸出變量,G(s)為被控時滯對象,K(s)表示解耦器,C(s)表示控制器。H(s)不包含時滯部分。
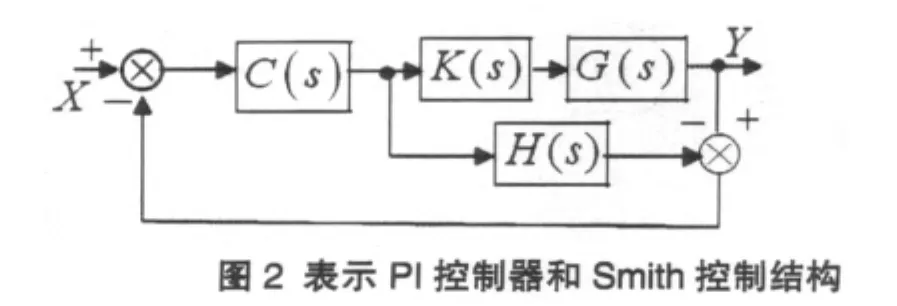
圖 3 中 C(s)為 PI控制器,K(s))G(s))為被控制對象的傳遞函數,先假設二個通道相互獨立,用Simulink軟件仿真,仿真圖如4所示,其中C(s)的參數,積分系數Sp1為27,比例系數Si1為0.2.第二個通道Sp2為8,Si2為0.8.Input1值為3的階躍信號,Input2值為2的階躍信號。
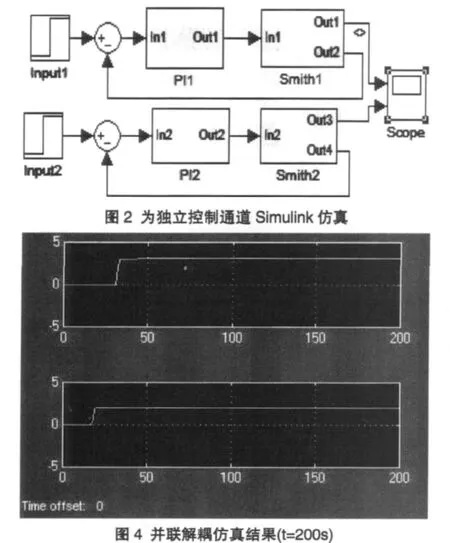
PI為控制器,其內部的 Si1,為 0.2,Sp1為 27。
最后得出的仿真結果穩定性比較好。如圖5所示。
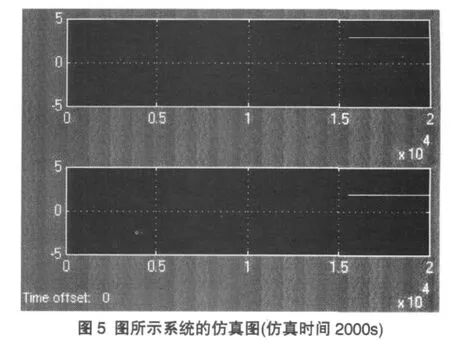
2 并聯補償法(PCD)設計
在工業自控系統中的2輸入2輸出系統中,由于系統多個通路之間存在著相互耦合,并且當系統的復雜性增大以后,傳統的解耦方法并不能十分有效地解決這個問題,所以本文利用一種新的方法——并聯補償法,在耦合項加上一項大小相同但方向相反的耦合項,使得耦合項的作用大大減小。
該 仿 真 實 驗 時 間 分 別 為 t=200,400,600,800,1000,2000,8000,10000,20000s,在仿真之后,比較并聯補償法與對角解耦法的優勢。
3 結論
本文使用了一種新的解耦方法,從上面的例子可以看出,并聯解耦比對角解耦的要求的條件更低,而且穩定性能更好。對角矩陣要求受控對象的矩陣必須是可逆的,但是并聯解耦矩陣卻沒有這方面的要求。顯示出了并聯解耦法的優點。
[1]金以慧,方崇慧.過程控制[M].北京:清華大學出版社,1993.
[2]謝任宏.MATALAB R2008控制系統動態仿真實例[M].北京:化學工業出版社,2009.
[3]翁怡方.自動控制理論[M].北京:機械工業出版社出版,2007.
[4]劉豹.現代控制理論[M].北京:機械工業出版社,1992.

