冷彎矩形管主要成型道次的FEM模擬

胡盛德，張雪峰，劉 勇，馬 力，鄭劍峰，王 絹，汪雯婕

（武漢科技大學鋼鐵冶金及資源利用省部共建教育部重點實驗室，湖北武漢，430081）

冷彎矩形管由于其自重輕、截面經濟、精度高、表面光潔和環保被廣泛用于鋼結構件和漿體運輸領域［1－2］，然而冷彎矩形管主要成型過程所存在的復雜性，使得其仍是一門經驗性很強的工程技術。業內不少學者采用有限元法模擬冷彎成型過程，探討模擬計算參數對冷彎成型計算結果的影響，這些研究成果雖為冷彎成型過程的定性分析起到很好的作用［3－6］，但因缺少現場生產數據以及材料模型和成型過程型鋼性能的實驗數據，使得模擬成型與實驗成型存在相當差距。

為此，本文基于ANSYS－APDL參數化設計語言，以現場冷彎母材拉伸實驗數據建立本構模型，對冷彎矩形管主要成型過程進行FEM模擬，以期為冷彎矩形管成型過程的工藝優化提供依據。

1 設計對象與模擬流程

本文模擬軟件結構的設計對象為某型鋼廠15道次厚壁矩形管冷彎成型過程，其中性面輥花工藝如圖1所示。由圖1可看出，冷彎成型過程模擬分為5個部分：第1部分為1～4道次，即板帶平整和兩頂角發生的主要彎曲變形；第2部分為5～8道次，即兩底角發生的主要彎曲變形；第3部分為9～11道次，即頂底角同時發生的剩余微小變形；第4部分為擠壓高頻焊接；第5部分為12～15道次，即焊管形狀的精整。

冷彎成型過程模擬流程如圖2所示。計算過程按照上述5個部分進行。

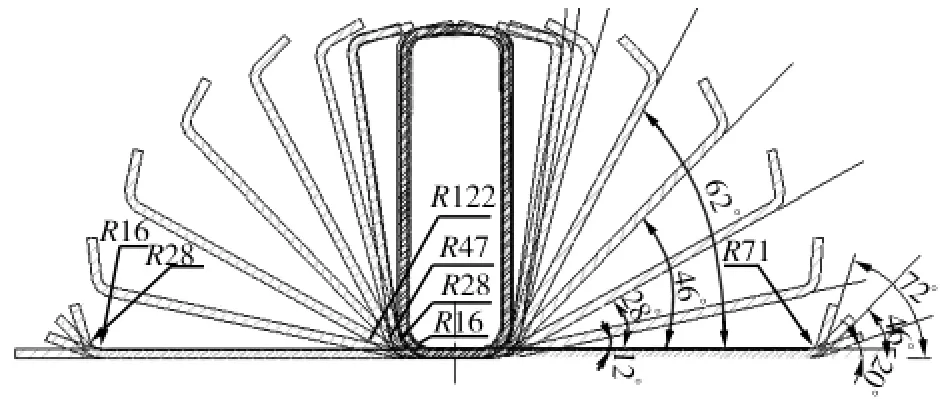
圖1 矩形焊管冷彎輥花工藝Fig.1 Cold－forming process of a rectangular steel tube

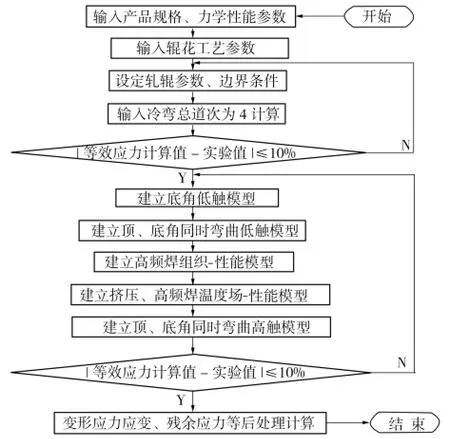
圖2 冷彎成型仿真流程Fig.2 Simulating process of cold－rolled forming

2 模型描述

2.1 材料本構關系模型

冷彎板帶材料本構關系模型直接關系到模擬結果的正確與否。以某熱軋Q345鋼帶為原料，沿寬度方向取樣，經拉伸實驗后繪制成實驗應力－應變曲線，再編制程序擬合雙線性硬化模型。當實驗數據與雙線性模型對應數據點流動應力差的平方和最小時，認為獲得最佳模型，FEM模擬時取若干試樣雙線性模型參數的平均值。圖3為母材試樣實驗雙線性模型的擬合結果。

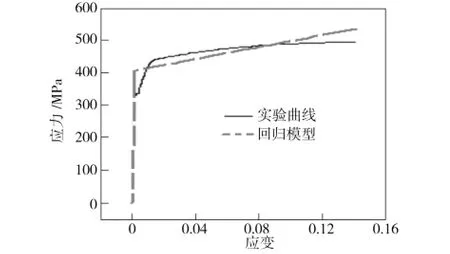
圖3 母材試樣實驗雙線性模型擬合曲線Fig.3 Bilinear model fitting curves of parent metal

2.2 幾何模型與FEM模型

輸入材料屬性和幾何參數，包括母材雙線性屈服強度、彈性模量、切線模量以及板料長度、寬度和厚度等參數，加上上述5個部分的不同成型參數，包括機架間距、輥徑、道次彎曲角、彎曲半徑和道次接觸等，建立幾何模型。為了節省空間和提高計算速度，考慮板料和軋輥的對稱性，取其1／2進行建模計算，圖4為冷彎變形2～8道次的幾何模型。

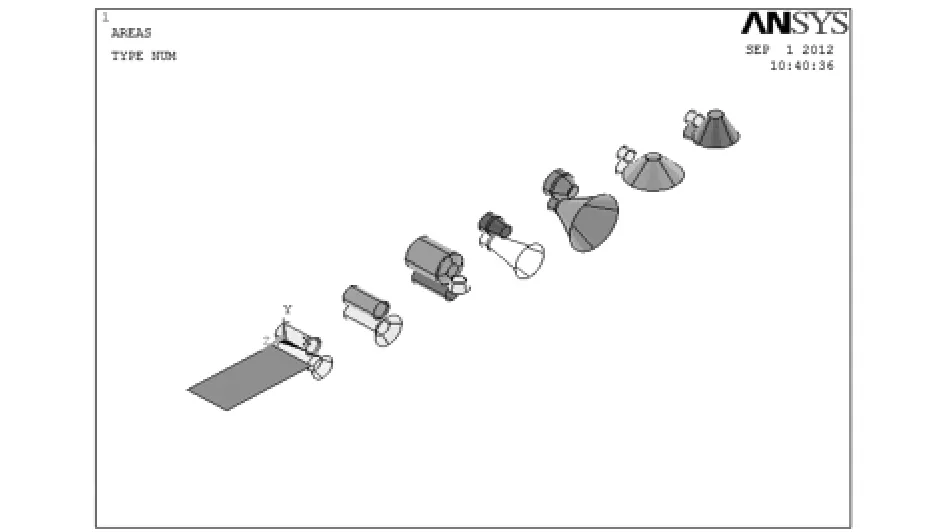
圖4 冷彎主要變形道次的幾何模型Fig.4 Geometric model of main deformation in cold forming

對板料和軋輥均采用薄殼四節點四邊形單元SHELL163進行網格劃分后，得到FEM模型。將沿殼厚方向積分點參數NIP設置為5，母材本構關系為雙線性硬化模型（BKIN）。將軋輥定義為剛性體，每個軋輥由一個PART控制，軋輥數量由輸入的軋制道次和軋輥類型通過循環程序控制。板料與軋輥之間采用庫侖摩擦模型，其靜摩擦系數和動摩擦系數分別取0.2和0.1。冷彎成型的第2、4、7道次軋輥FEM模型如圖5所示。

圖5 軋輥FEM模型Fig.5 FEM modeling for rollers

3 模擬結果與討論

模擬冷彎產品為200 mm×300 mm×9.2 mm高頻感應矩形焊管，結果表明成型第1道次的板帶切邊平整，沒有引起帶鋼的塑性變形［7］，故本文不作模擬。研究還表明，頂角經過第2～4道次冷彎，其強度達到擠壓焊接前該位置最高強度的96%；底角經過第5～8道次冷彎，其強度達到擠壓焊接前該位置最高強度的91%，主要冷彎變形在前8道次發生［7］。因此，本文利用開發的程序，對冷彎第2～8道次進行模擬。為了驗證模擬結果，根據輥花工藝和模擬計算參數編制程序，在冷彎成型模擬完成后，提取歷經每個道次后彎角部位各節點的最大等效應力。將本文彎角部分節點等效應力模擬平均值與文獻［7］中所測量的彎角試樣屈服應力進行比較，其結果如圖6所示。由圖6可看出，模擬等效應力與實驗值相吻合，最大相對誤差小于9%。

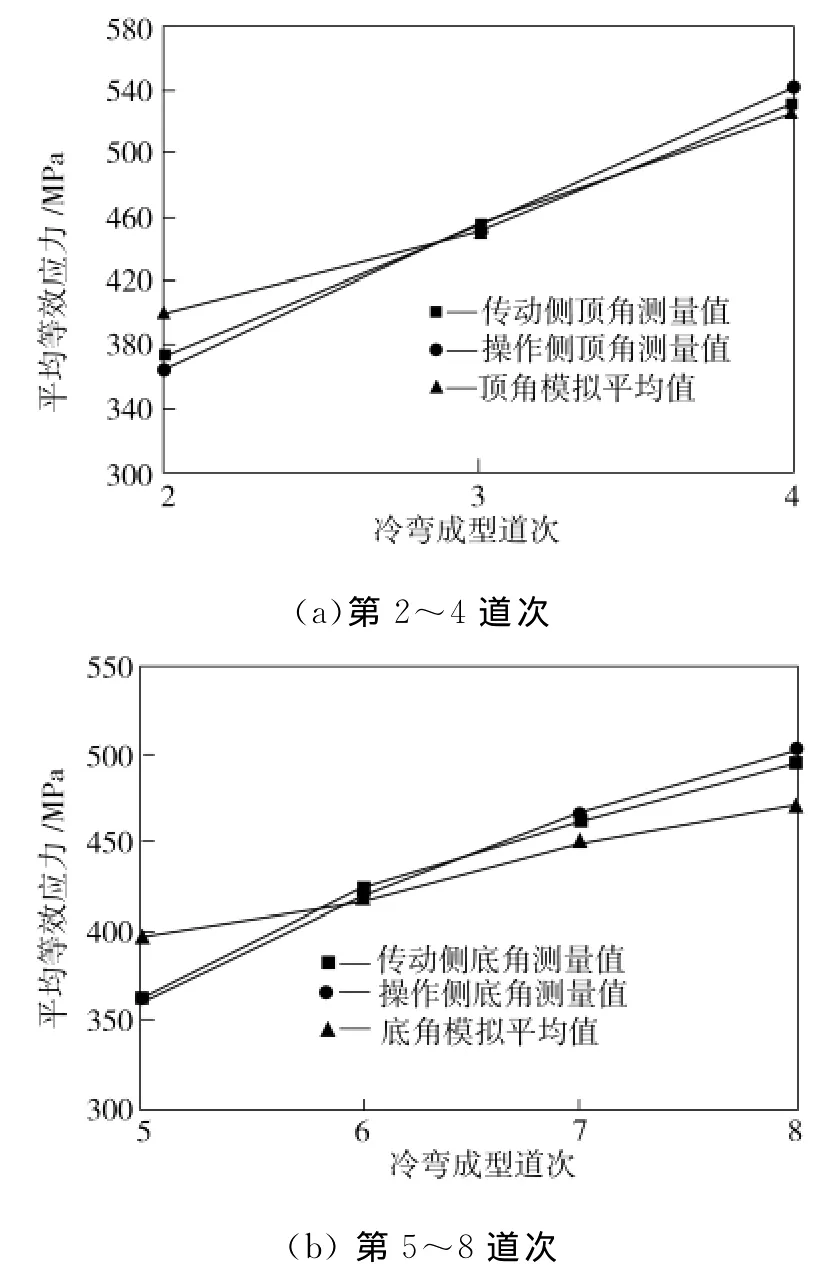
圖6 彎角等效應力模擬與實驗值比較Fig.6 Comparison between simulated effective stresses and measured values in corner portion

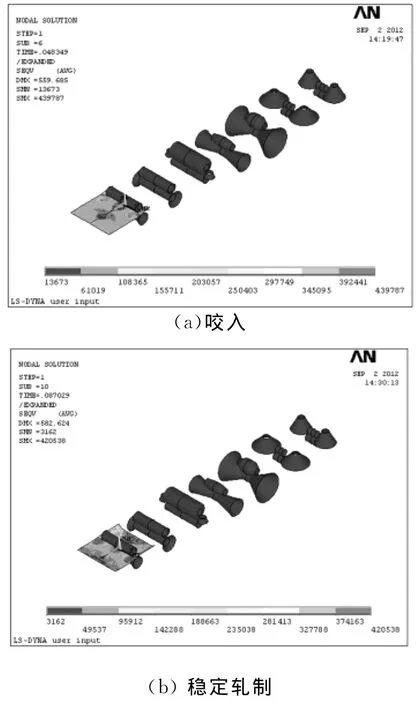
圖7 第2道次變形等效應力云圖Fig.7 Effective stress field in Pass 2

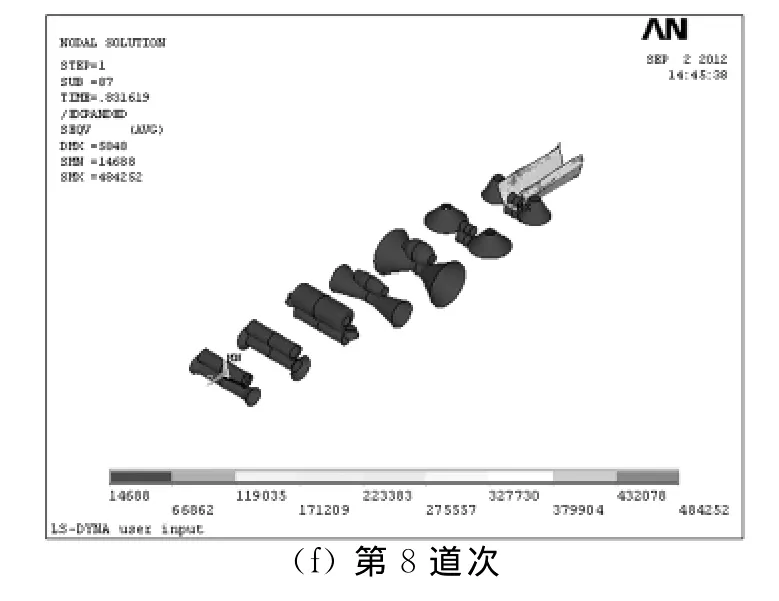
圖8 各道次變形等效應力云圖Fig.8 Effective stress field in different passes

圖7～圖8為模擬各道次的等效應力云圖。由圖7可看出，第2道次剛咬入時，彎角變形區附近等效應力最大，高頻焊對面的中央平板局部以及帶鋼邊部等效應力次之，彎角部位發生了明顯的塑性變形，中心局部區域發生了小量塑性變形，其他部位仍處于彈性變形階段。第2道次穩定冷彎階段，邊部高應力區范圍擴大，鋼帶邊部不少區域進入塑性變形狀態。由圖8可看出，其他道次的等效應力分布變化規律類似于第2道次，但隨著應變程度的增加，邊部和彎角部位高應力區域和塑性變形區域的范圍進一步擴大，帶鋼頭部出離輥道后的不規則回彈清晰可見。

表1為2～8道次冷彎后彎角部位節點塑性等效應變平均值。由表1可看出，冷彎成型第2～4道次彎角部位總的等效塑性應變值為0.36。道次等效塑性變形主要在第3、4兩個道次完成，共計0.302，占第2～4道次全部應變的83.88%，其中第4道次等效塑性應變增加量最大，占54.44%。第5～8道次等效塑性應變的變化規律類似于第2～4道次，第8道次等效塑性應變增量最大。輥花參數符合道次參數分配的一般規律：在變形角選擇上，開始道次選取稍小，中間道次要盡可能大，后面道次則越小越好。但計算表明，此工藝參數值不是最好，因為第4、8道次等效塑性應變增加量過大，而第3、6、7道次等效塑性應變相對較小。為達到軋輥磨損均勻，減少換輥時間，又能生產較好的板形，避免出現翹曲褶皺等缺陷，應盡量保證板料在中間各個道次等效塑性應變要大，但應變增量相差不要過大。由此可看出，適當地增加第3、6、7道次的變形角，可使鋼管變形和軋機負荷達到更加均勻。

表1 彎角道次等效應變平均值Table 1 Mean effective strains in the corner portion

4 結語

基于冷彎成型過程的實驗，在建立連續輥彎成型模擬軟件結構的基礎上，利用ANSYS－APDL語言開發了冷彎成型過程FEM模擬程序，對冷彎主要變形道次進行模擬計算，模擬計算結果與實驗結果相吻合，模擬軟件可用于輥花設計與冷彎工藝優化。

［1］ Q V Buia，J P Ponthot.Numerical simulation of cold roll－forming processes［J］.Journal of Materials Processing Technology，2008，202（1）：275－282.

［2］ A Alsamhan，P Hartely，I Pillinger.The computer simulation of cold－roll－forming using FE methods and applied real time re－meshing techniques［J］.Journal of Materials Processing Technology，2003，142（1）：102－111.

［3］ C D Moen，T Igusaa，B W Schafer.Prediction of residual stresses and strains in cold－formed steel members［J］.Thin－Walled Structures，2008，46（1）：1 274－1 289.

［4］ 胡斯堯，李立新，彭娟.基于BP網絡的冷彎型鋼軋后回彈預報模型［J］.武漢科技大學學報：自然科學版，2006，29（5）：446－448.

［5］ 曾國，來新民，于忠奇，等.多道次輥彎成形數值模擬技術［J］.上海交通大學學報，2007，41（10）：1 598－1 602.

［6］ 胡盛德，羅惟，陳楠，等.連續輥彎成形過程模擬研究［J］.武漢科技大學學報，2010，33（5）：468－470.

［7］ 胡盛德，李立新，周家林.冷彎厚壁矩形型鋼管冷彎效應［J］.建筑結構學報，2011，32（6）：76－81.