無(wú)金標(biāo)準(zhǔn)條件下含協(xié)變量的ROC曲線估計(jì)方法*
劉 妍 王紅宇 田嬌妮 劉桂芬△
無(wú)金標(biāo)準(zhǔn)條件下含協(xié)變量的ROC曲線估計(jì)方法*
劉 妍1王紅宇2田嬌妮1劉桂芬1△
目的闡明無(wú)金標(biāo)準(zhǔn)條件下,考慮協(xié)變量后估計(jì)ROC曲線的兩部貝葉斯模型。方法 介紹兩部貝葉斯模型,結(jié)合實(shí)例,篩選無(wú)金標(biāo)準(zhǔn)條件下ROC曲線的影響因素,考慮協(xié)變量影響后,估計(jì)ROC曲線。結(jié)果 兩部貝葉斯模型不僅可探討協(xié)變量對(duì)疾病狀態(tài)的影響,而且可探討協(xié)變量對(duì)診斷試驗(yàn)結(jié)果的影響,同時(shí)可計(jì)算不同協(xié)變量取值條件下ROC曲線下面積。結(jié)論 兩部貝葉斯模型可有效地解決無(wú)金標(biāo)準(zhǔn)條件下,考慮協(xié)變量影響的ROC曲線估計(jì)問(wèn)題。
兩部貝葉斯模型 ROC曲線 無(wú)金標(biāo)準(zhǔn) 協(xié)變量
*:國(guó)家自然科學(xué)基金項(xiàng)目(編號(hào)81172774);山西省自然科學(xué)基金項(xiàng)目(編號(hào)2009011005-2)
1.山西醫(yī)科大學(xué)衛(wèi)生統(tǒng)計(jì)教研室(030001)
2.山西醫(yī)科大學(xué)第二醫(yī)院
△通訊作者:劉桂芬,E-mail:liugf66@gmail.com
診斷試驗(yàn)是臨床研究的重要組成部分,它可在篩檢試驗(yàn)的基礎(chǔ)上,進(jìn)一步把患者、疑似病例和需鑒別的其他疾病區(qū)別開(kāi)來(lái),且病人的療效評(píng)價(jià)、預(yù)后估計(jì)等在一定程度上也都依賴于診斷試驗(yàn),所以科學(xué)地評(píng)價(jià)診斷試驗(yàn),可提供給患者關(guān)于疾病的可靠信息、影響醫(yī)生制定治療計(jì)劃,有效避免不必要的資源浪費(fèi)。受試者工作特征曲線(receiver operating characteristic curve,ROC曲線)是目前評(píng)價(jià)診斷試驗(yàn)常用的一種方法,有關(guān)含協(xié)變量的ROC曲線分析,一般方法都必須基于金標(biāo)準(zhǔn)存在的假設(shè)。然而在許多疾病狀態(tài)下,由于“金標(biāo)準(zhǔn)”不存在或十分昂貴或執(zhí)行起來(lái)不符合實(shí)際,有時(shí)很難甚至不可能建立一個(gè)權(quán)威的“金標(biāo)準(zhǔn)”。這使在許多ROC曲線分析中,不自覺(jué)地采用不完善評(píng)價(jià)診斷試驗(yàn)標(biāo)準(zhǔn),從而導(dǎo)致估計(jì)的ROC曲線估計(jì)偏差加大。
本文擬闡明一種無(wú)金標(biāo)準(zhǔn)條件下考慮協(xié)變量影響后,估計(jì)ROC曲線的方法——兩部貝葉斯模型,它可在考慮協(xié)變量對(duì)疾病狀態(tài)影響的同時(shí),考慮協(xié)變量對(duì)診斷試驗(yàn)結(jié)果的影響,并可計(jì)算不同協(xié)變量取值條件下ROC曲線下面積(AUC),從而進(jìn)行不同試驗(yàn)準(zhǔn)確度的比較。
兩部貝葉斯模型原理
兩部貝葉斯模型(two-part bayesian model)首先篩選影響疾病狀態(tài)的協(xié)變量,該過(guò)程可用logistic回歸模型來(lái)擬合;第二個(gè)過(guò)程即篩選影響試驗(yàn)結(jié)果的協(xié)變量,該過(guò)程可采用線性模型來(lái)擬合。
隨機(jī)抽取含量為n的樣本,設(shè)第i個(gè)個(gè)體(i=1,…n),Di(Di=0或1)為其客觀但未知的二分類疾病狀態(tài),Ti為目標(biāo)診斷試驗(yàn)的試驗(yàn)結(jié)果,Ri為采用不完善標(biāo)準(zhǔn)(參照試驗(yàn))進(jìn)行診斷的試驗(yàn)結(jié)果(Ri=1:陽(yáng)性,Ri=0:陰性)。假定兩試驗(yàn)相互獨(dú)立,即在Di條件下Ti與Ri相互獨(dú)立。
對(duì)于第 i個(gè)個(gè)體,設(shè)有 K 個(gè)協(xié)變量 Xi,1,…,Xi,K,可能影響疾病狀態(tài)Di或目標(biāo)診斷試驗(yàn)結(jié)果Ti,或者二者都受影響。令 Xi=(1,Xi,1,…,Xi,K)',為篩選影響疾病狀態(tài)的協(xié)變量,建立logistic回歸模型,定義為:
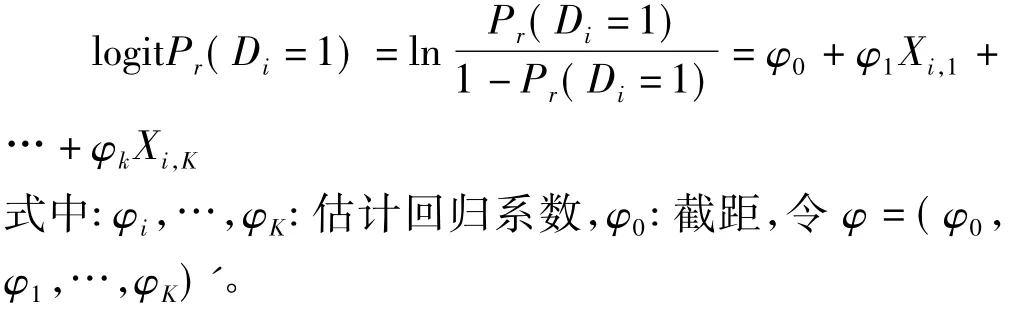
為篩選在Di條件下,影響目標(biāo)試驗(yàn)結(jié)果Ti的協(xié)變量,建立Ti條件均值線性模型,記作:

式中:p:任意截?cái)帱c(diǎn)處的(1-特異度),α={E(Ti|Di=1)-E(Ti|Di=0)}/σD,β = σH/σD,由此計(jì)算得到的ROC曲線下面積記作:
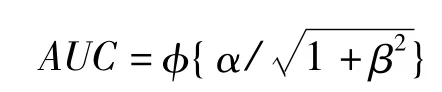
對(duì)于參照試驗(yàn)結(jié)果Ri,建立自然誤分類模型(naturemisclassification model),模型如下:
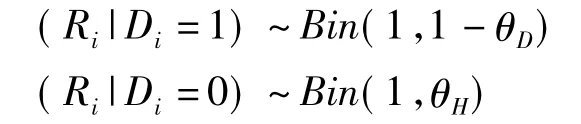
式中:θD和θH:該參照試驗(yàn)的假陰性率和假陽(yáng)性率,二者同樣也是未知的。對(duì)于第i個(gè)個(gè)體,Di、Ti與Ri的聯(lián)合似然函數(shù)表示為:

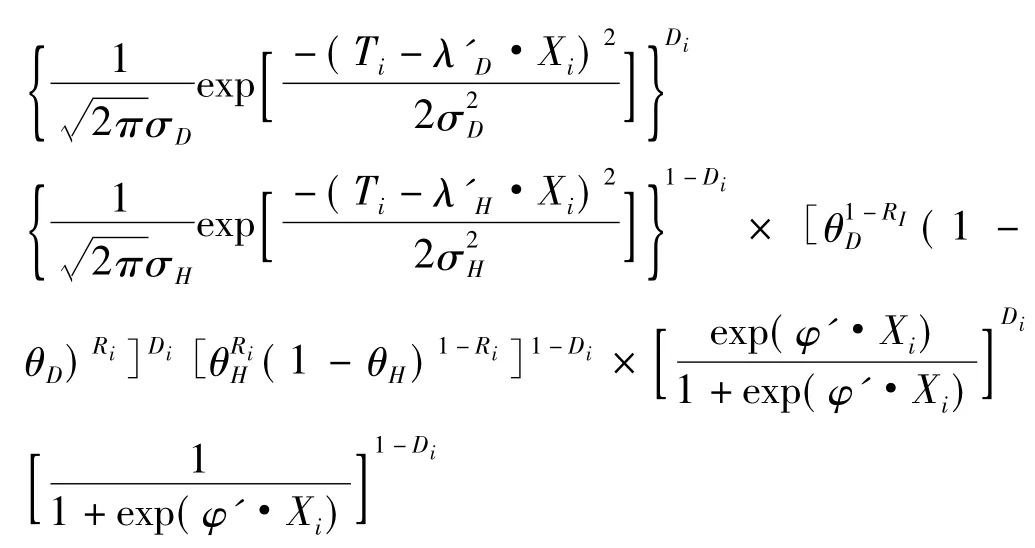
為每個(gè)參數(shù)設(shè)定先驗(yàn)分布,假定 λD、λH、1/σ、1/σ、θD、θH和 φ 的先驗(yàn)分布相互獨(dú)立。對(duì)于每個(gè) λD,0,λD,1…λD,K、λH,0,λH,1…λH,K和 φ0,φ1…φK選用正態(tài)無(wú)信息先驗(yàn)分布 N(0,1000),1/σ和 1/σ選用伽馬無(wú)信息先驗(yàn)分布γ(0.001,0.001),θD和 θH選用貝塔無(wú)信息先驗(yàn)分布β(0.5,0.5)。根據(jù)先驗(yàn)分布和似然函數(shù),采用MCMC方法得出后驗(yàn)分布的參數(shù)估計(jì)值。本研究使用Gibbs抽樣構(gòu)造馬爾科夫鏈來(lái)模擬參數(shù)的后驗(yàn)分布,得到所有待估參數(shù)的完全條件分布。根據(jù)估計(jì)獲得的模型參數(shù),繪制出協(xié)變量取值分層的多條ROC曲線,并計(jì)算相應(yīng)的ROC曲線下面積,進(jìn)而準(zhǔn)確地評(píng)價(jià)該指標(biāo)分層診斷的價(jià)值。整個(gè)過(guò)程應(yīng)用MATLAB7.8實(shí)現(xiàn)。
模擬研究
在金標(biāo)準(zhǔn)D和參照標(biāo)準(zhǔn)R對(duì)應(yīng)的θD、θH均已知的情況下進(jìn)行模擬,隨機(jī)產(chǎn)生服從兩部貝葉斯模型要求的隨機(jī)變量T,條件均值結(jié)構(gòu)為

式中,X1,X2均服從均勻分布,X1,X2~ U(0,1),(T|D=1),(T|D=0) ~ N(0,1)。取 θD=0.1,θH=0.2 進(jìn)行模擬研究,采用兩部貝葉斯模型進(jìn)行分析,取無(wú)信息先驗(yàn)分布(如前文),模擬50000次,退火算法(burnin)迭代次數(shù)取5000次,退火后迭代次數(shù)即 Monte Carlo樣本量為45000,參數(shù)估計(jì)結(jié)果見(jiàn)表1和表2。
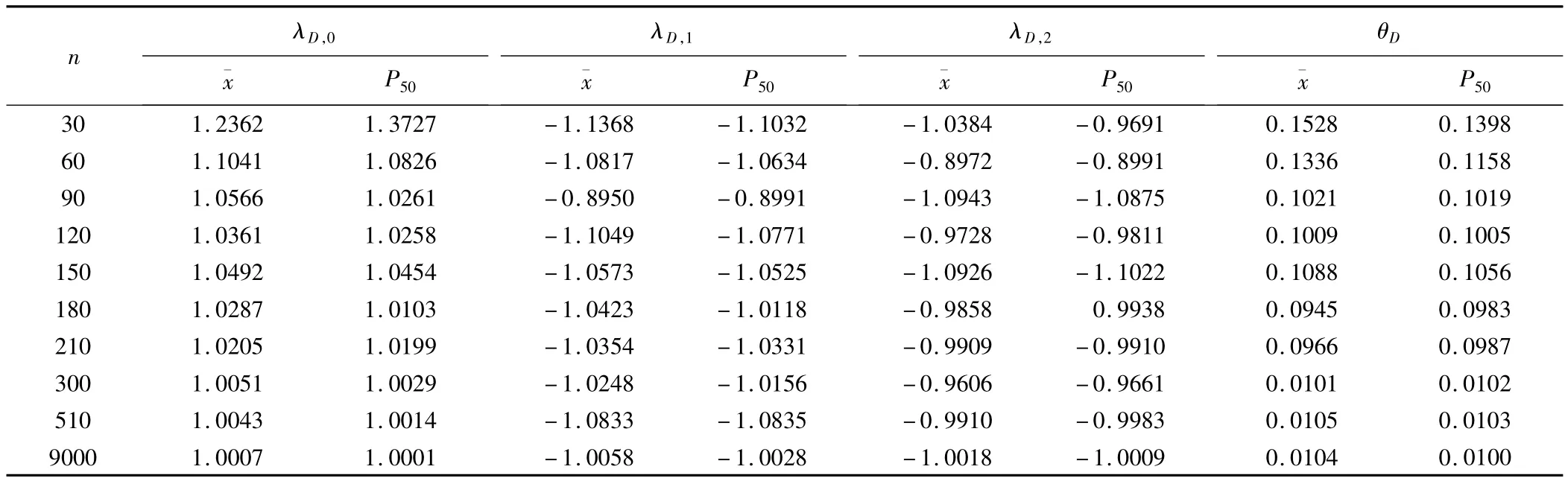
表1 兩部貝葉斯模型模擬研究參數(shù)估計(jì)結(jié)果分析(1)
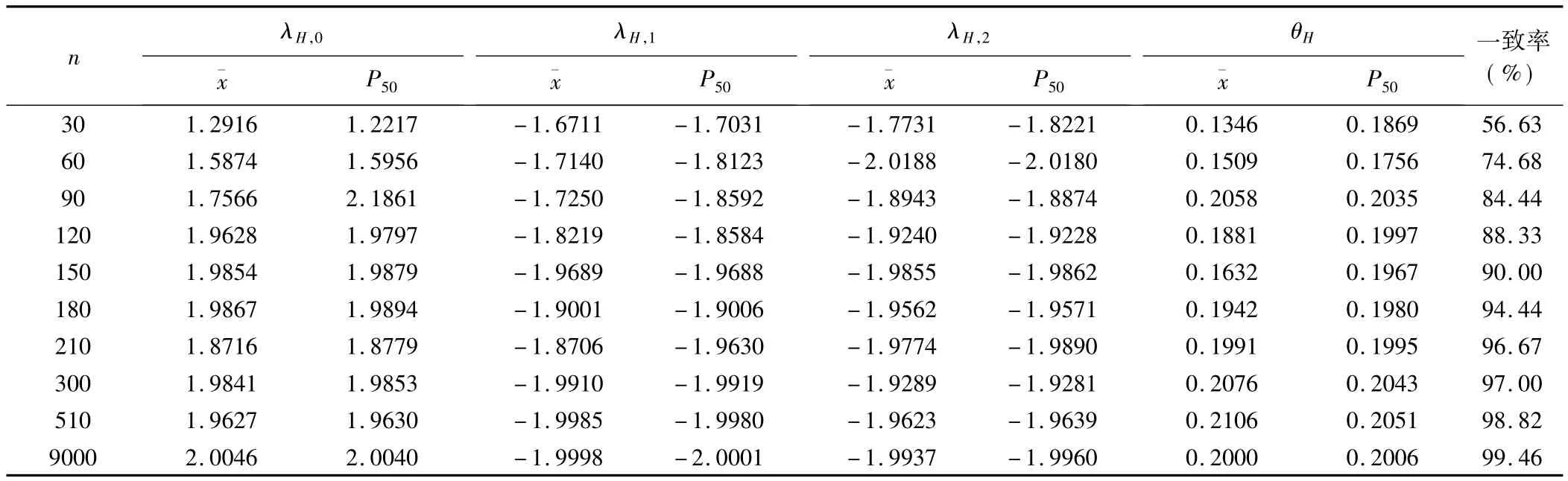
表2 兩部貝葉斯模型模擬研究參數(shù)估計(jì)結(jié)果分析(2)
由表模擬結(jié)果可見(jiàn):(1)隨樣本含量的增加,參數(shù)估計(jì)的準(zhǔn)確度越來(lái)越好,當(dāng)樣本含量增加到150時(shí),參數(shù)估計(jì)值與真值接近,但Chong Wang等人研究表明,為了將居住環(huán)境、生活習(xí)慣等混雜因素對(duì)診斷結(jié)果的影響降到最小,應(yīng)在允許的范圍內(nèi)盡量抽取不同居住地、不同生活習(xí)慣的樣本,也即盡可能增大樣本含量。(2)兩部貝葉斯估計(jì)的中位數(shù)和均數(shù)雖相差不大,但中位數(shù)更接近真實(shí)值。(3)在樣本含量低于100時(shí),模型估計(jì)得到的值與設(shè)定的真實(shí)值的一致率不足85%;當(dāng)樣本含量逐漸增大到150時(shí),二者的一致率達(dá)90%;當(dāng)樣本含量大于300時(shí),參數(shù)估計(jì)結(jié)果幾乎與真值接近。由此可見(jiàn),兩部貝葉斯模型對(duì)于無(wú)金標(biāo)準(zhǔn)條件下考慮協(xié)變量后的ROC曲線估計(jì),方法可行,結(jié)果準(zhǔn)確,樣本含量在150例以上,診斷試驗(yàn)準(zhǔn)確度更高。
實(shí)例分析
國(guó)際公認(rèn)只有冠狀動(dòng)脈造影(CAG)才是冠心病診斷的金標(biāo)準(zhǔn)。但由于CA G術(shù)是利用導(dǎo)管對(duì)冠狀動(dòng)脈解剖進(jìn)行的放射影像學(xué)檢查,屬一種創(chuàng)傷性介入診斷技術(shù),患者依從性較差,這為接受冠心病的診斷試驗(yàn)帶來(lái)困難。欲在未進(jìn)行CAG檢查條件下,正確地對(duì)冠心病做出診斷,本研究收集了有臨床癥狀自我感覺(jué)不適的疑似冠心病患者168例,檢測(cè)其收縮壓、甘油三酯含量,并以心電圖作為參照標(biāo)準(zhǔn)。以24h動(dòng)態(tài)心電圖(Holter)中心率變異指標(biāo)——竇性心搏RR間期標(biāo)準(zhǔn)差(SDNN),作為診斷區(qū)分冠心病的主要指標(biāo)。收集分析數(shù)據(jù)與統(tǒng)計(jì)描述結(jié)果見(jiàn)表3。
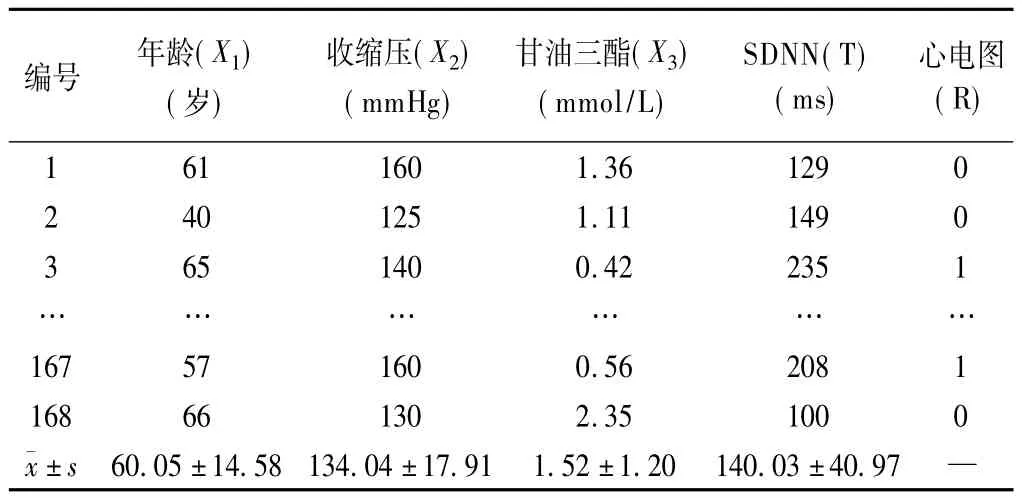
表3 168例疑似冠心病患者部分檢測(cè)結(jié)果及統(tǒng)計(jì)描述表
采用MCMC法進(jìn)行模型參數(shù)估計(jì),先驗(yàn)分布選取無(wú)信息先驗(yàn),如前文,模擬50000次,退火算法迭代次數(shù)取5000次,退火后迭代次數(shù)即Monte Carlo樣本量為45000,按所得金標(biāo)準(zhǔn)分組的統(tǒng)計(jì)描述及分析結(jié)果見(jiàn)表4和表5。
表4 168例疑似冠心病患者各指標(biāo)統(tǒng)計(jì)描述(±s)

表4 168例疑似冠心病患者各指標(biāo)統(tǒng)計(jì)描述(±s)
指標(biāo) 冠心病患者(n=53) 非冠心病患者(n=115)31收縮壓(mmHg) 138.47±19.24 131.99±16.96甘油三酯(mmol/L) 2.14±1.55 1.23±0.87 SDNN(ms) 118.30±42.83 150.04±36.年齡(歲) 62.08±15.10 59.11±14.07
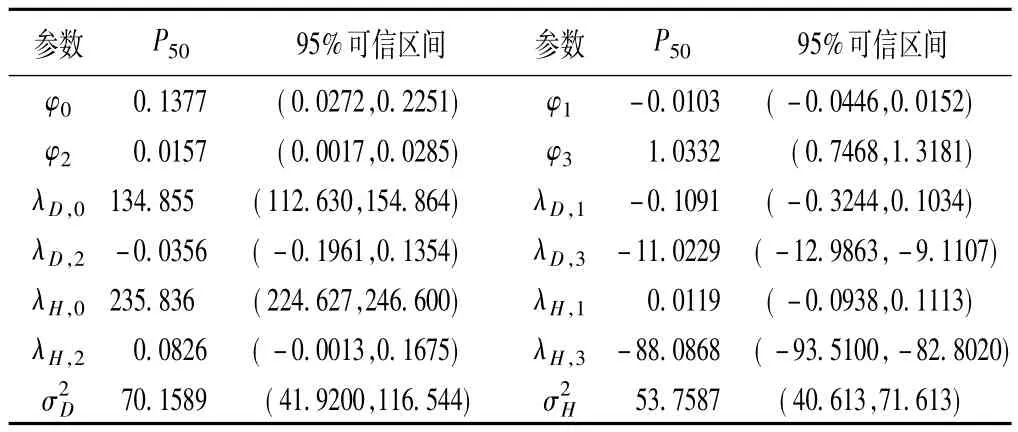
表5 SDNN診斷冠心病參數(shù)估計(jì)結(jié)果
由表5結(jié)果可見(jiàn),參數(shù)φ2和φ3的95%可信區(qū)間未包括0,可以認(rèn)為收縮壓和甘油三酯含量是影響冠心病患病與否的因素,兩指標(biāo)95%可信區(qū)間均大于0,表明冠心病患者組的收縮壓和甘油三酯含量均高于對(duì)照組;λD,3和 λH,3的 95% 可信區(qū)間未包括 0,表明甘油三酯含量對(duì)SDNN診斷冠心病有影響,二者均小于0,表明甘油三酯含量越高,對(duì)應(yīng)的SDNN值越小,心率變異越小。同時(shí),尚不能認(rèn)為協(xié)變量年齡和收縮壓是心率變異SDNN診斷冠心病時(shí)的有意義因素。
若以甘油三酯含量分層,繪制相應(yīng)的ROC曲線(見(jiàn)圖1)可見(jiàn),甘油三酯含量越高,相應(yīng)的ROC曲線下面積越大;AUC分別為0.7965、0.8359和0.8792,變化較為明顯,表明甘油三酯含量在SDNN診斷冠心病方面,對(duì)診斷結(jié)果準(zhǔn)確性有較大影響。甘油三酯含量偏離正常值越遠(yuǎn),SDNN用于冠心病診斷的準(zhǔn)確性就越高。
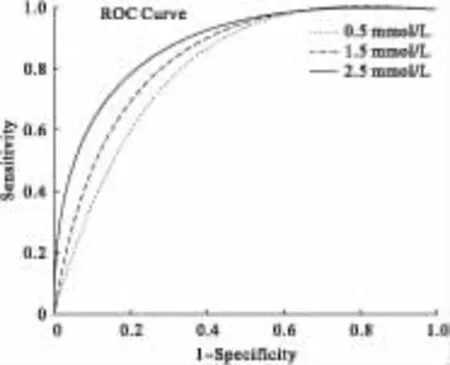
圖1 不同甘油三酯下SDNN診斷冠心病的ROC曲線
討論與小結(jié)
1.兩部貝葉斯模型對(duì)于無(wú)金標(biāo)準(zhǔn)條件下考慮協(xié)變量后的ROC曲線估計(jì),方法可行,結(jié)果準(zhǔn)確
模擬研究結(jié)果表明,隨樣本含量的增加,兩部貝葉斯模型對(duì)于無(wú)金標(biāo)準(zhǔn)條件下考慮協(xié)變量后的ROC曲線估計(jì),參數(shù)估計(jì)的準(zhǔn)確度越來(lái)越好,當(dāng)樣本含量增加到150時(shí),參數(shù)估計(jì)值與真值接近。在樣本含量低于100時(shí),模型估計(jì)得到的值與設(shè)定的真實(shí)值的一致率不足85%;當(dāng)樣本含量逐漸增大到150時(shí),二者的一致率達(dá)90%;當(dāng)樣本含量大于300時(shí),參數(shù)估計(jì)結(jié)果與真值接近。
2.兩部貝葉斯模型作為無(wú)金標(biāo)準(zhǔn)條件下的診斷試驗(yàn)?zāi)P停奢^好地解決冠心病的診斷問(wèn)題
24 h動(dòng)態(tài)心電圖(Holter)作為無(wú)創(chuàng)檢查很易被大家接受,但一直被臨床工作者認(rèn)為,不能作為有價(jià)值的診斷指標(biāo)。SDNN是24 h動(dòng)態(tài)心電圖心率變異的一項(xiàng)基礎(chǔ)指標(biāo),容易檢測(cè)。實(shí)例分析結(jié)果可見(jiàn),在考慮協(xié)變量對(duì)疾病狀態(tài)影響的同時(shí),考慮了協(xié)變量對(duì)診斷試驗(yàn)結(jié)果影響的兩部貝葉斯模型,可作為無(wú)金標(biāo)準(zhǔn)條件下,冠心病診斷準(zhǔn)確性達(dá)到80%左右的無(wú)創(chuàng)診斷指標(biāo)。本研究將影響診斷結(jié)果的甘油三酯含量納入模型,得到含量偏離正常值(<1.7mmol/L)越遠(yuǎn),診斷準(zhǔn)確性越高的結(jié)論,解釋更接近臨床實(shí)際,并可計(jì)算出不同甘油三酯含量條件下,ROC曲線診斷的準(zhǔn)確度。
3.兩部貝葉斯模型對(duì)反應(yīng)變量分布沒(méi)有特定要求
通常的ROC分析,反應(yīng)變量若不服從雙正態(tài)分布,需要對(duì)數(shù)據(jù)進(jìn)行轉(zhuǎn)換,而兩部貝葉斯模型對(duì)于反應(yīng)變量不服從雙正態(tài)分布的情況,可以通過(guò)改變第二個(gè)過(guò)程的擬合模型來(lái)解決,對(duì)于反應(yīng)變量分布沒(méi)有特定要求。
兩部貝葉斯模型作為無(wú)金標(biāo)準(zhǔn)診斷試驗(yàn)?zāi)P停粌H可考慮協(xié)變量的影響,同時(shí)可較好地解決無(wú)金標(biāo)準(zhǔn)時(shí)疾病的診斷問(wèn)題。模擬研究表明,基于MCMC算法的貝葉斯估計(jì),參數(shù)估計(jì)結(jié)果準(zhǔn)確。SDNN是考慮甘油三酯含量影響后,冠心病無(wú)創(chuàng)診斷試驗(yàn)穩(wěn)健性更好的一項(xiàng)診斷指標(biāo)。有關(guān)含有缺失值的兩部貝葉斯模型估計(jì),建議采用隨機(jī)缺失數(shù)據(jù)多重填補(bǔ)后,再進(jìn)行參數(shù)估計(jì),討論見(jiàn)另文。基于MCMC算法的貝葉斯估計(jì),退火迭代次數(shù)應(yīng)保證迭代鏈達(dá)到收斂,結(jié)果可由模擬結(jié)果迭代圖來(lái)判斷。若不能達(dá)到收斂,就不可進(jìn)行參數(shù)估計(jì),需考慮修正模型或者選擇其他形式的先驗(yàn)分布(見(jiàn)另文)。
1.Zhou XH.Statistical methods in diagnostic medicine.New York:John Wiley & Sons,2002.
2.O'Malley AJ,Zou KH,F(xiàn)ielding JR,et al.Bayesian regression methodology for estimating a receiver operating characteristic curve with two radiologic applications.Academic Radiology,2001,8(8):713-725.
3.Wang C,Turnball BW,Grohn YT,et al.Estimating receiver operating characteristic curves with covariates when there is no perfect reference test for diagnosis of Johne's disease.American Dairy Science Association,2006,89:3038-3046.
4.Goetqhebenr E,liinev J,Boelaert M,et al.Diagnostic test analyses in search of their gold standard:latent class analyses with random effects.Statistical Methods in Medical Research,2000,9(3):231-248.
5.Pepe MS.A regression modelling framework for receiver operating characteristic curves in medical diagnostic testing.Biometrika,1997,84:595-608.
6.宇傳華.ROC分析方法及其在醫(yī)學(xué)研究中的應(yīng)用.陜西:第四醫(yī)科大學(xué)(博士論文),2000.
7.陳衛(wèi)中,潘小平,倪宗瓚.Logistic回歸模型在ROC分析中的應(yīng)用.中國(guó)衛(wèi)生統(tǒng)計(jì),2007,24(1):22-24.
Estimating Receiver Operating Characteristic Curves with Co- variates in the Absence of Gold Standard Test
LiuYan,WangHongyu,TianJiaoni,etal.TheDepartmentofHealthStatistics,ShanxiMedicalUniversity(030001),Taiyuan
ObjectiveTo introduce the method for estimation of receiver operating characteristic curves with covariates when there is no gold standard test.MethodsTo estimate the ROC curve after considered the effects of covariates,using two-part Bayesian model screening the impact factors for the ROC curve without gold standard test.ResultsTwopart Bayesian model can detect the impact of covariates not only on disease status but also on test scores.Moreover,the areas under the ROC curve with different values of covariates could be calculated.The method was also treated as the proof of statistical analysis for clinical diagnostic test.ConclusionTwo-part Bayesian model can be effectively used to solve the problem of estimating ROC curves impacted by covariates when there is no gold standard test.
Two-part Bayesian model;ROC curve;No golden standard test;Covariate;
 中國(guó)衛(wèi)生統(tǒng)計(jì)2012年3期
中國(guó)衛(wèi)生統(tǒng)計(jì)2012年3期
- 中國(guó)衛(wèi)生統(tǒng)計(jì)的其它文章
- 臨床試驗(yàn)中多重性問(wèn)題的統(tǒng)計(jì)學(xué)考慮
- 職業(yè)學(xué)校學(xué)生心理健康影響因素研究*
- 醫(yī)學(xué)院校生考試焦慮與應(yīng)對(duì)方式的相關(guān)研究
- 不同人群的SNPs基因型數(shù)據(jù)中r2值對(duì)TagSNP數(shù)量的影響*
- 有監(jiān)督的主成分分析和偏Cox回歸模型在基因數(shù)據(jù)生存預(yù)測(cè)中的應(yīng)用*
- 縱向監(jiān)測(cè)連續(xù)非隨機(jī)缺失數(shù)據(jù)變系數(shù)模型及其應(yīng)用*
