有監督的主成分分析和偏Cox回歸模型在基因數據生存預測中的應用*

覃 婷 王 彤

當用基因表達數據預測生存情況時，基因數遠遠超過了樣本例數。除了高維度以外，基因表達之間通常存在著某種未知的相關，其增加了解釋變量之間的共線性?；虮磉_數據存在的小樣本、高維度、強相關的特點給生存預測帶來了困難。因此根據基因數據做生存預測時，首先需要對基因表達數據進行降維或者調整，從而更加有效而準確的進行參數估計。有監督的主成分分析(supervised principal component analysis，SuperPC)和偏 Cox回歸(partial least squares Cox regression)是其中的兩種降維方法。本文將通過模擬研究和對國際上公開的三個基因數據集進行分析，以探討這兩種方法用于高維數據生存預測表現的優劣，為得到更精確的預后估計和改進治療策略提供依據。

基本原理與方法

1.基因微陣列數據的標識與比例風險模型

假設有一組包含著截尾數據的基因微陣列生存數據有 n 個個體，(yi，δi，xi);i=1，…，n。其中 yi為個體i的失效時間，yi可以是完全數據，也可是截尾數據;δi是一個指示變量，當δi=1時為完全數據，而當δi=0為截尾數據;xi=(xi1，…，xip)T為個體i的自變量向量。

令Y為生存時間。生存函數定義為S(y)=P(Y＞y)，是某個體在時間y時刻依然存活的概率。風險函數測量在y時刻存活的個體，在下個很小的時間段內死亡的瞬時風險。比例風險模型表示為

h(y，X)=h0(y)exp(XTβ) (1)其中h0(y)是一個非指定的基準風險函數。

模型的參數向量^β通常可以取最大偏對數似然得到，基準生存函數H0(y)可用Breslow估計，表示為 ^H0(y)。對于一個表達譜為~X的新樣本，根據已知的參數和基線風險估計求出其風險函數和生存函數，

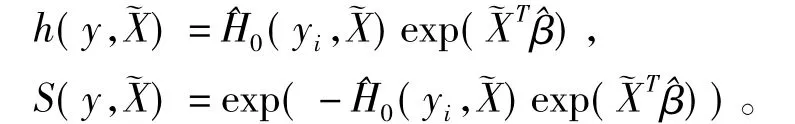
2.有監督的主成分分析

SuperPC 是由 Bair和 Tibshirani等人提出的〔1－2〕，它改進常規主成分分析無法保證所選擇的主成分與病人的生存相關的缺點，在降維的時候考慮了生存時間，其核心思想就是只對與生存時間密切相關的基因進行主成分分析。

該方法首先將每一個基因分別代入單變量Cox模型h(t|x)=h0(t)exp(βx)，以檢驗它們對生存的影響。然后對其進行基于偏似然函數的參數估計與假設檢驗，檢驗方法為似然比檢驗。將基因按照檢驗所得到的P值從小到大排序，然后根據交叉驗證法挑選出前λ1百分比的基因組成一個簡化矩陣Xθ。采用奇異值分解法(singular value decomposition，SVD)對這個簡化矩陣進行主成分分析。

假設X矩陣的列已經被中心化，均數為0。那么n×p矩陣X的奇異值分解寫作:

其中U是一個n×n的正交陣，V是p×p正交陣，D是一個以奇異值dj為對角元素的n×p對角陣，r=min(n，p)是X的秩，非零奇異值的數目與X矩陣的秩相等，d1≥d2≥…≥dr＞0。

那么，簡化矩陣Xθ的奇異值分解寫作:

令 Uθ=(uθ，1，uθ，2，…，uθ，r)，稱 uθ，1為 X 的第一有監督的主成分，依此類推。如果僅取一個成分，即擬合一個應變量為y和自變量為uθ，1的Cox比例風險模型，得

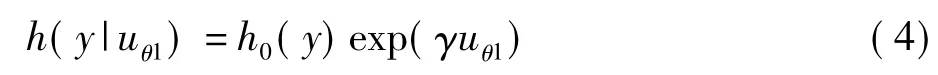
從公式(3)變換得到(注意到正交陣V'V=I)，

因為 uθ，1是 Xθ的一個線性組合:uθ，1=Xθwθ，1，所以模型(4)可以看作是一個利用了Xθ中的所有自變量的受限模型:

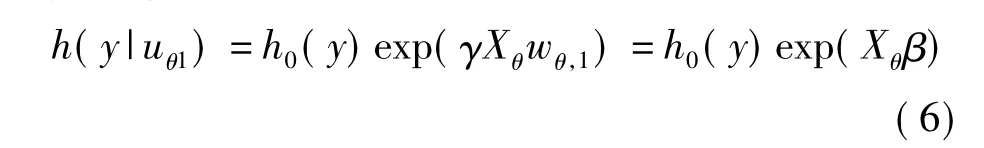
假如有一個新的基因數據集x*，對其進行生存預測，步驟如下:

3.偏Cox回歸

在基因數據的生存預測方法中，基于偏最小二乘的生存分析是一個重要的家系。利用偏最小二乘方法進行降維，即從原始變量中提取偏最小二乘成分，然后將提取的這些線性成分應用于標準的Cox回歸進行生存預測的方法，就稱之為偏Cox回歸。

偏Cox回歸算法有很多種，這里采用的是Nyg?rd提出的算法〔3〕。該算法主要是通過將生存問題轉換為廣義線性回歸問題，然后依照廣義線性模型的迭代再加權偏最小二乘算法提取PLS成分，從而實現高維數據的降維，然后將所得到的參數估計以及提取的PLS成分代入Cox比例風險模型中，進行生存預測。由于這種算法將基準風險增量的估計與PLS降維分開，使得PLS的成分僅為基因表達譜的線性組合，更符合生物解釋。

由于該算法只是對^η進行了部分更新，可解決收斂速度過慢的問題。且分開估計協方差效應和基線風險增量避免了數據維度的擴張，加上提取的PLS成分數量小，所以計算速度通常很快，節約了計算時間。

4.根據交叉驗證法選擇模型調整參數

預測方法的模型復雜程度是由估計調整參數來決定的。調整參數的估計方法有很多種，最經常使用的就是交叉驗證。在本文中，我們采用Verweij和van－Houwelingen提出的交叉驗證準則〔4〕，這種準則是建立在Cox偏對數似然的基礎上的。

首先將數據分成等大小的K個部分(1＜K≤n)，每個第i(1≤i≤K)次的交叉驗證都會將第i個層剔除，只用剩下的層來訓練模型，根據訓練好的模型來估計被剔除的第i個層的預測信息，重復K次，這樣每一個部分都做了并且只做了一次驗證組。令l(β)表示全部數據的Cox對數似然，l(－i)(β)表示剔除第i個層數據的對數似然，將第i個部分對似然的貢獻定義為li(β)=l(β) － l(－i)(β)，使得 l(－i)(β)最大化的 β 估計值表示為β^(－i)。假設似然成分是獨立的，那么li(β)就簡單的等于第i個部分的貢獻，并且l(β)，K折交叉驗證的最大對數似然為 CVL =，隨著λ的變化，每個最大對數似然CVL也在變化，其中最大的CVL所對應的λ為最優調整參數。

在實踐中，通常會給出調整參數的范圍，在給定的范圍內找最優調整參數。SuperPC的調整參數λ=(λ1，λ2)是雙變量的，λ1代表單變量分析中與生存時間有關的基因子集占基因全集的百分比，λ2代表將要選擇的主成分數的范圍。

5.模型評價

一般來說，預報因子的真正性能評價應該用一個獨立的數據來完成。但是在缺乏獨立數據的情況下，可以通過交叉驗證來進行模型評價，即將每一個數據集按2:1的比例隨機分成訓練數據集和驗證集。訓練組樣本的基因表達和生存數據被用來構建預測模型，驗證集用來評估模型的性能。為了避免依賴于訓練集和驗證集的選擇，需進行重復分組，以所有評價標準的結果的中位數和四分位數間距來估計預測模型的性能。本論文主要的評價標準為決定系數R2。

決定系數是驗證組中的生存數據可以被預報因子解釋的那部分變異所占的百分比。預測性能良好的預報因子可以解釋驗證組生存數據的絕大部分變異。在傳統的回歸背景下，R2=1－殘差平方和/總平方和，因此它的取值范圍在0到1之間。然而這個定義在數據存在刪失的情況下不能使用，因此，Nagelkerke給出了一個可以用在Cox比例風險模型中R2統計量〔5〕

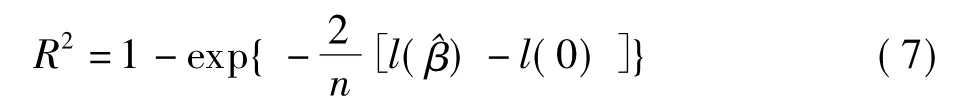
其中l(．)表示對數似然函數。R2越大，預報器的預測性能越好。

模擬分析

為了進一步驗證上述模型的預測性能，我們根據基因數據的特點設計了模擬實驗，用上述方法對模擬實驗產生的數據進行分析，根據模型預測評價標準對它們的預測性能進行比較。模擬條件設定如下:

(1)協變量矩陣X:

生成100×1000的基因協變量矩陣，每一行表示一個病人，每一列表示一個基因。這些協變量服從多元正態分布，均數向量為0。將數據分成十塊等大小的基因塊∑b，令它們的方差協方差矩陣的對角元素為，非對角元素為。因此∑對應于基因表達的類別，這樣不同類別的基因表達是獨立的，但是在同一個類別中的基因表達有同樣的兩兩相關。在模擬中，我們令ρ分別等于0.3，0.6，0.9以觀察不同相關程度對結果的影響，同時評判三種不同方案的方差:(a)=…==1，即所有的基因表達的方差相等，(b)==2，=…==1，即前兩塊的基因表達的變異更大，(c)==1/2=…==1，即前兩塊的基因變異比其他塊的要少。

我們首先產生服從(0，1)均勻分布的隨機數S，令生存函數S(t)=S，利用用產生相應的生存時間t。

(4)生成刪失指示變量:

產生一組隨機數，服從二項分布，發生1的概率為0.8，也就是截尾為20%，為了觀察截尾比例是否對降維方法產生影響，我們改變了截尾比例，截尾比例分別為20%，50%。

按照上述的實驗設計產生訓練組數據，然后以同樣的條件產生驗證組數據。分別應用SuperPC和偏

(2)參數的設定:

每個回歸系數對應于它對應變量的影響。在本文中，參數的設定如下:當 1≤j≤100，βj=0.01，當 101≤j≤200，βj從0.01 到0.1，每0.01 為一個步長。201≤j≤1000，βj=0，表示在基因矩陣中只有少數一些相關的協變量，大部分的協變量都是無關的。

(3)生成生存時間:Cox回歸方法對訓練組進行建模，然后用驗證組數據進行預測評價，在最優調整參數的條件下評價模型的預測性能，評價標準為R2，從評價標準的中位數以及離散程度來對模型進行評價。以上過程重復200次。模擬結果以箱式圖矩陣表示。

箱式圖矩陣的行代表影響生存的前兩塊基因的方差，列代表3個不同的相關系數。spcr為SuperPC方法，pls為偏Cox回歸方法。censored=0.2和censored=0.5分別表示刪失比例為20%和50%的模擬數據的結果。

由圖1可見，根據模型評價標準，SuperPC的預測性要優于偏Cox;當相關系數相同時，兩種方法得到的R2都是隨著方差的增大而增大，提示基因的方差越大的時候，基因塊越容易被識別。方差相同時，相關系數越大，得到的R2越大。隨著截尾比例的增大，模型的預測性能會變差，說明模型的預測能力會受到刪失比例的影響。

實例分析

用上述兩種方法對國際上三個公開的基因數據集進行了分析，它們分別是Van't Veer等的乳腺癌數據〔6〕，78個病人，4 751個基因，觀察事件的結局是乳腺癌是否轉移，截尾比例為56.4%;Beer等人的肺癌數據集〔7〕有86個病人和7 129個基因，觀察事件結局為死亡，截尾比例為72.6%;Bullinger等人急性髓系白血病(acute myeloid leukemia)的數據〔8〕，116 個病人，6 283個基因，觀察事件結局為死亡，截尾比例為42.24%。

因為對于每個數據集，采用不同的評價標準，最佳的預測方法有可能是不同的〔9〕。因此，對于一個實例數據，首先要看用這兩種方法進行分析的預測性能如何，然后根據預測結果挑選合適的預測模型。

首先按2:1的比例將數據隨機分成訓練組和驗證組:訓練組用于構造模型，而驗證組用來對模型的預測性能進行評價。為了保證預測結果評價的客觀性，避免數據任意分割導致的預測偏差，按上述方法重復將數據集隨機分割200次。結果見圖2。

圖中bc代表乳腺癌數據，lc代表肺癌數據，aml代表急性髓系白血病數據，spcr為是SuperPC方法的分析結果，pls為偏Cox方法的分析結果。

R2值越大，模型可以解釋數據的變異部分越大，模型的預測性能越好。從圖2中我們可以看到，對于乳腺癌數據，SuperPC方法的表現要優于偏Cox回歸。而對于肺癌數據和急性髓系白血病數據，則偏Cox回歸的表現要優于SuperPC方法。

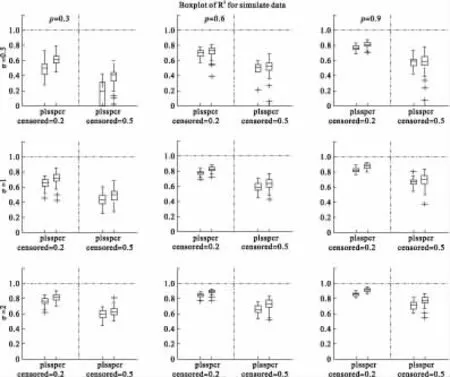
圖1 模擬數據分析結果矩陣圖

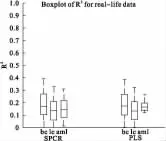
圖2 實際數據分析結果圖

因為我們對這3個數據進行了隨機分割(分割成訓練集和驗證集)，分割了200次，每次分割得到的最優調整參數的取值是不一樣的。因此，這里我們給出了三個實例數據分析中，兩種方法各自所選擇的最優調整參數的分位數的表。

從表1中我們可以看到，SuperPC提取的成分數大于等于偏Cox回歸，并且提取的成分數不穩定。SuperPC提取的基因子集占原基因集的比例很小，即簡化矩陣遠小于原始矩陣。所以雖然SuperPC引入的成分數多，但每個成分中包含的自變量數目要少于全基因集。偏Cox方法提取的成分數穩定，用很少的成分就可以解釋原始變量的大部分變異。

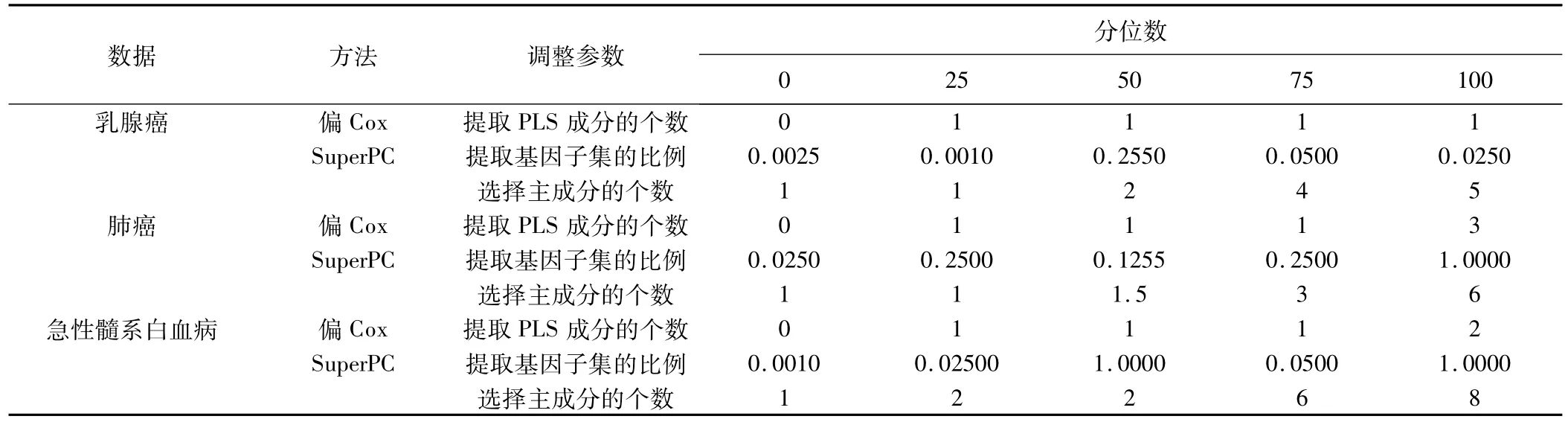
表1 實際數據分析中選擇的最優調整參數的分位數

根據上面的模型預測性能評價，挑選各個數據對應的最適方法來對整個數據集進行了模型擬合就得到了預測方程。可以計算預后指數來估計病人的預后情況，預后指數的公式為PI=X^β。當得到新的病人的基因數據~X的時候，就可以根據預后指數PI=~X^β來對其分類:按照預后指數的中位數，將病人分成兩組，預后指數超過中位數的，為高危組，可考慮相對積極的治療策略;低于中位數的，為低危組，可以采用相對保守的治療方案。

討 論

有監督的主成分分析和偏Cox回歸都是將Cox比例風險模型與降維技術結合起來，適用于基因數據的生存預測。這兩種方法都對主成分回歸進行了改進，利用了應變量的信息。它們的區別在于有監督的主成分分析是對基因子集進行特征提取，而偏Cox回歸則是對基因的全集進行特征提取。

從模擬實驗中可見:(1)隨著影響生存的基因塊的方差的增大，兩種方法的預測性能變好，這是因為當自變量的變異更大的時候，被提取的信息也更多，可提高回歸估計的精度和穩定性，故而當影響生存的基因塊的方差大的時候較容易被識別出來。(2)隨著組內相關系數ρ的增高，兩種方法的預測性能都變好。因為只有存在著相關，才能夠把維度降下來，特征值會隨著相關的增高而增大，那么前幾個主成分的方差就會很大，這樣只需要幾個主成分，就能夠很好的解釋原始變量的變異。隨組內相關系數的增高，預測方法性能變好的同時還應注意到，當基因的相關度較高的時候，預測方法對選擇正確的基因比較不敏感，對生存沒有影響卻與對生存有影響的基因高度相關的基因也可能被納入。(3)隨著刪失比例的增加，兩種方法的預測性能變差，說明預測方法會受到刪失比例的影響。

在實例分析中，根據判斷標準，不同的數據集最優預測方法不同。模擬研究和實例分析中，有監督的主成分分析提取的成分數要大于等于偏Cox回歸。然而我們也應該注意到，因為這種主成分是有監督的，所以雖然引入的成分數多，但每個成分中包含的自變量數目要少于全基因集。

在我們的模擬研究中，這兩種方法的預測性能很好，用我們的模型能夠解釋原始變量的變異比例較大，決定系數甚至達到了0.9的情況。但是，實例分析中可以看到，決定系數沒有那么大。造成這種差異的原因可能是因為模擬實驗設計的時候，基因塊之間設定了相關系數，各個基因塊中的基因兩兩相關，而基因塊之間不相關，并且對回歸參數也進行了設定，只是前兩塊基因與生存有關，數據生成具有一定的規律。而實際的微陣列數據遠比模擬數據要復雜得多，基因之間以未知的方式相關，并且微陣列數據中的協變量數千至數萬個，簡單的模擬不能夠捕獲這種復雜的關系。并且模擬中為了計算的方便，只是模擬了1 000個協變量，樣本含量固定取100個，這與實際微陣列數據的樣本含量和自變量個數相比，樣本含量的比例要大得多。實例數據分析，因為是隨機拆分數據，最后得到的訓練組數據和驗證組數據的截尾比例可能會比原來的數據要高，這也是影響結果的一個原因之一。

在模擬研究中，有監督的主成分分析的預測性能要優于偏Cox回歸。但本文介紹的偏Cox回歸算法因其在收斂性上進行了改進，從而計算速度很快，比有監督的主成分分析方法節約了很多時間。對于高維數據的分析來說，計算時間短也是個很重要的優點。

1.Bair E，Tibshirani R.Semi－supervised methods to predict patient survival from gene expression data.PLoS Biology，2004，2:511－522.

2.Bair E，Hastie T，Paul D，et al.Prediction by supervised principal components.Journal of the American Statistical Association，2006，101:119－137.

3.Nyg?rd S，Borgan O，Lingiaerde OC，et al.Partial least squares Cox regression for genome－wide data.Lifetime Data Anal，2008，14:179－195.

4.Verweij PJMvan，Houwelingen HC，Cross－validation in survival analysis.Stat Med，1993，12:2305－2314.

5.Nagelkerke NJS.A note on a general definition of the coefficient of determination.Biometrika，1991，78:691－692.

6.Van't Veer LJ，Dai H，Van de Vijver.Gene expression profiling predicts clinical outcome of breast cancer.Nature，2002，415:530－536.

7.Beer DG，Kardia SL，Huang CC，et al.Gene－expression profiles predict survival of patients with lung adenocarcinoma，2002，Nat Med 8:816－824.8.Lars Bullinger MD，Konstanze D?hner MD，Eric Bair，et al.Use of geneexpression profiling to identify prognostic subclasses in adult acute myeloid leukemia.Massachusetts Medical Society，2004，350 16:1605－1616.

9.W.van Wieringen，D.Kun，R.Hampel，et al.Survival prediction using gene expression data:a review and comparison.Computational Statistics and Data Analysis，2009，53:1590－1603.