基于幅度補償的MVDR水下噪聲源近場定位識別方法研究

陳 歡，何 良，楊德森，時勝國

（1.中國艦船設計研究中心，武漢 430026；2.哈爾濱工程大學 水聲技術國家級重點實驗室，哈爾濱 150001）

由于艦船的結構龐大、系統復雜，對它的噪聲治理除了要對其進行噪聲測量與分析，了解其噪聲特性；另一個關鍵問題就是找出在系統中起主要作用的噪聲源，即噪聲源的定位識別。艦船噪聲主要分布在低頻段［1］（100 Hz～1 kHz）。因此如何在低頻段獲得比較理想的空間分辨率及有效描述系統噪聲源的能量分布，成為艦船噪聲源定位識別的關鍵技術。

聲聚焦陣列信號處理方法適用于大尺度、復雜系統的噪聲源定位識別，常規近場聚焦波束形成是其典型代表。常規近場聚焦波束形成是根據聲源到達各個陣元曲率半徑不同，按球面波規律進行相位補償，根據基陣與聲源的位置重建測量平面，給出噪聲源的空間位置分布。常規近場聚焦波束形成因其優良的寬容性和易操作性得到了國內外專家學者的廣泛研究和應用［2－4］。但其空間分辨率受到基陣孔徑的限制，及處理信號頻率過高會引起空間混疊。MVDR算法［5－6］是在保持期望信號幅值不發生畸變的條件下，使整個系統輸出的能量最小，因此將MVDR算法應用于水下噪聲源近場定位中，通過相位補償可以實現水下噪聲源近場高分辨定位［7－8］，且有效抑制處理信號頻率過高引起的空間混疊。常規近場聚焦波束形成及MVDR近場聚焦波束形成，在中高頻段能夠獲得比較理想的空間分辨率；但在低頻段其定位性能嚴重下降［9］。

在水下噪聲源近場測量模型中，同時存在幅度補償和相位補償，而上述文獻并沒有考慮幅度補償問題。因此無法有效描述系統噪聲源的能量分布，導致無法準確找到系統中的主要噪聲源，給減振降噪工作帶來困難。有關幅度補償問題還鮮有報道。

本文在MVDR近場聚焦波束形成的基礎上，根據球面波擴展規律修正功率譜輸出值，從而有效估計系統噪聲源的相對強度，同時還可以提高基陣在低頻段的空間分辨率，及在高頻段能夠有效抑制空間混疊、抑制背景噪聲。

1 水下噪聲源近場測量模型

水下噪聲源近場測量模型如圖1所示，假設平面S緊貼被測系統表面，可以認為噪聲均從假想面S發出。因此，只要分析噪聲源在S面上的空間分布，就可以達到識別系統表面噪聲源的目的。

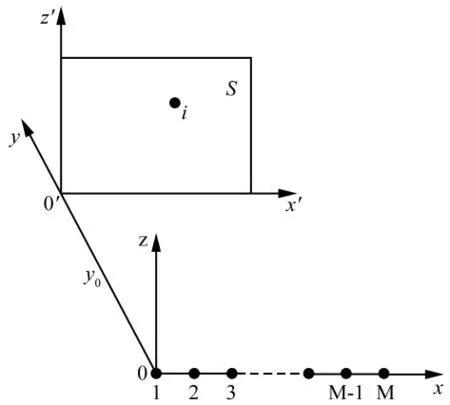
圖1 水下噪聲源近場測量模型Fig.1 Near-field measurements of underwater noise source model

假設被測平面S上存在點聲源i，其空間位置為（xi，y0，zi），M元聲壓水平器構成均勻水平陣放置于x軸正向，且一號陣元放置于原點處，陣元間距為d，基陣與平面S的距離（測量距離）為y0，點源i發射信號頻率為fi，背景噪聲為高斯白噪聲，則第m個聲壓水聽器接收的信號可以表示為：

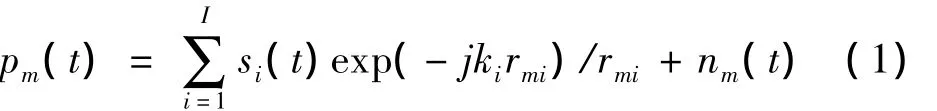
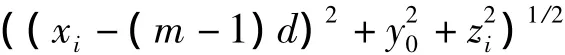
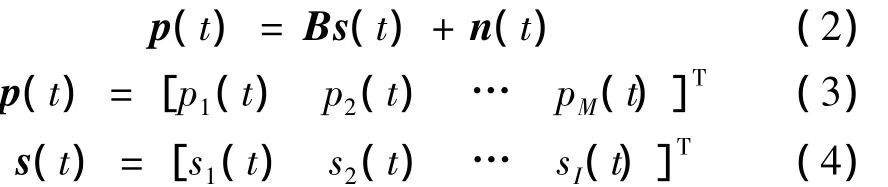
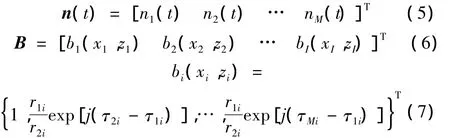
B表示基陣的陣列流形。在近場測量模型下，基陣接收到的信號幅度相位不一致，即在處理時需要考慮幅度補償及相位補償。

2 MVDR噪聲源近場定位識別方法

2.1 MVDR近場聚焦波束形成

wm表示加權值，則波束形成器的輸出可表示為以下的加權形式：

w=［w1，w2，…，wM］H，基陣輸入信號的協方差矩陣為R=E［p（t）p（t）H］。

a（x，z）表示掃描面上點（x，z）相對于基陣的相位補償向量，其形式為：

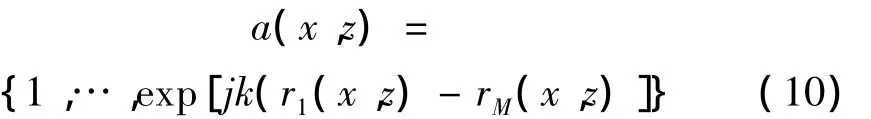
其中，k表示聲波的波數。利用拉格朗日常數法可以很方便的得到式（9）的最優權：

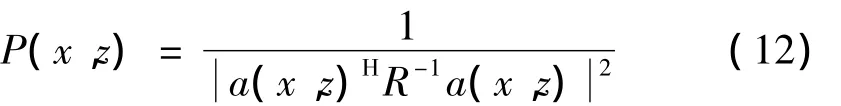
2.2 幅度補償MVDR近聚焦波束形成（ac-MVDR）

在近場測量模型下，基陣陣元間存在相位差及幅度差，因此在重建測量平面時應考慮幅度補償及相位補償，給出系統噪聲源的空間位置分布及相對能量分布。

wm表示加權值，則波束形成器的輸出可表示為以下的加權形式：

w=［w1，w2，…，wM］H，建立如下約束條件：

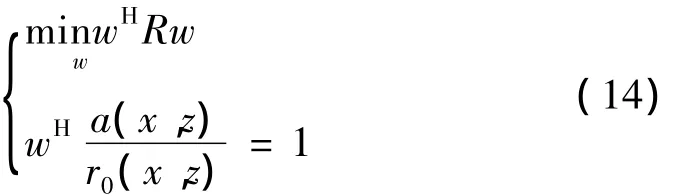
r0（x，z）表示掃描面上點（x，z）相對于基陣的歸一化幅度補償向量，其形式為：

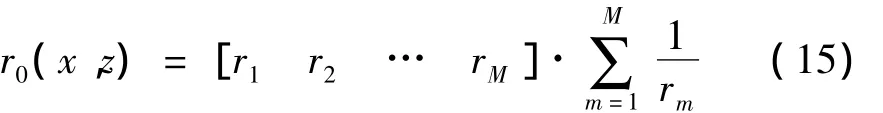
利用拉格朗日常數法可以很方便的得到式（14）的最優權：

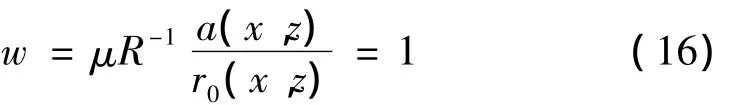
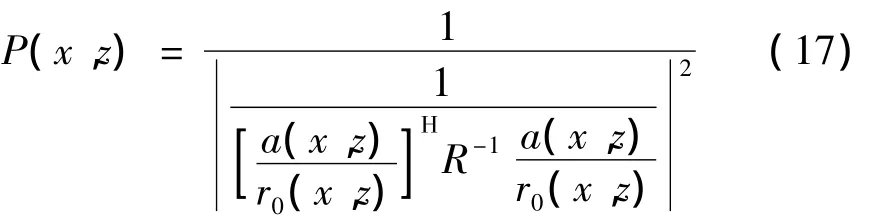
幅度補償是根據球面波擴展規律修正功率譜輸出值，將幅度補償向量歸一化可以避免補償過大引起的背景起伏，因此歸一化幅度補償的MVDR近場聚焦波束形成可以給出系統噪聲源的相對能量分布。

2.3 基于幅度補償的寬帶MVDR聚焦波束形成

文獻［10］介紹了基于子帶分解的MVDR水下噪聲源近場定位方法，通過仿真及實驗數據處理結果驗證了其有效性，但該方法無法實現寬帶相干噪聲源近場定位。本文介紹基于聚焦變換矩陣的寬帶信號源近場定位識別方法，該方法相比文獻［9］具有運算量相對較小、定位精度高、可處理相干信號源定位識別的優點。

假設觀測時間長度為T，將其分成K段（K定位為快拍數），每子段持續時間為T0，對每個子段數據進行離散傅立葉變換，將頻帶范圍f1～fJ劃分J個互不重疊的子帶，得到：

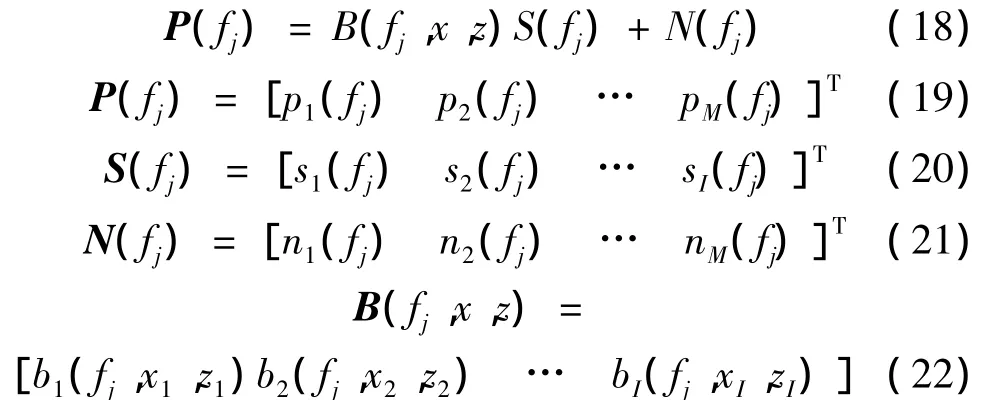
其中b（fj，xi，zi）為基陣相對于噪聲源（xi，zi）頻段fj的方向矢量。設T（fj）為聚焦變換矩陣，通過聚焦變換矩陣T（fj），使陣列方向矩陣B（fj，x，z）張成的子空間在Frobenius模最小意義下擬合 B（f0，x，z）張成的子空間，有：

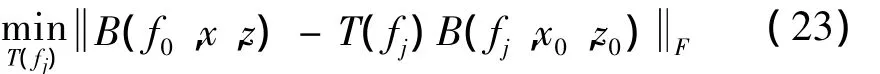
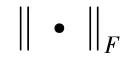
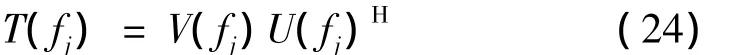
式中，U（fj）和V（fj）分別為B（fj，x，z）、B（f0，x，z）的左奇異矢量和右奇異矢量，具體的求解過程請參考文獻［11］。

利用上式就可以將頻帶內不重疊的頻率點上的信號空間聚焦到參考頻率點，聚焦后得到單一頻率點的數據協方差，再利用單頻信號的基于幅度補償的MVDR近場聚焦波束形成實現噪聲源定位識別。

3 計算機仿真實驗

假設20元聲壓水聽器構成的均勻水平陣，陣元間距1 m，測量距離為2 m，聲速1 500 m/s，背景噪聲為高斯白噪聲，采樣頻率為10 kHz，處理信號長度為1 s，掃描區域橫坐標為8 m～12 m、縱坐標為－8 m～8 m，步長為0.05 m。

3.1 單頻線譜定位識別結果分析

仿真實驗（強度不同雙聲源）：預設雙聲源位置分別為（8，0）、（10，0），兩聲源發射信號相互獨立，信噪比分布為20 dB、10 dB，結果如圖2、圖3所示。

3.2 寬帶信號定位識別結果分析

仿真實驗（強度相同雙聲源）：預設雙聲源位置分別為（9，0）、（11，0），發射信號的帶寬均為100 Hz～500 Hz，聚焦頻率為315 Hz，，信噪比均為10 dB，結果如圖4所示。

由圖2、圖3可得，MVDR近場聚焦波束形成在低頻段其定位性能嚴重下降，而通過幅度補償后可以大幅度的提高聚焦分辨率，且可實現系統噪聲源的相對強度估計，同時可以進一步抑制空間混疊。圖4驗證了本文方法通過聚焦變換可以實現寬帶相干信號源的近場高分辨定位識別。

3.3 不同測量距離下的幅度補償結果分析

但在近場測量模型下，隨著測量距離的增加，基陣的曲率變化相對較平緩，因此有必要分析測量距離對基于幅度補償的MVDR近場聚焦波束形成性能的影響。

由圖5可得，MVDR近場聚焦波束形成難以實現聲源相對強度估計，聲源相對強度估計偏差隨測量距離的減小而增大，即使在相對較遠的測量距離情況下，也會產生較大的估計偏差。

但基于幅度補償的MVDR近場聚焦波束形成，其聲源相對強度估計值并不依賴于測量距離，即使在聲源強度相差20 dB情況下，估計偏差也不會超過0.5 dB。

4 湖試實驗數據處理

本文所用到的實驗數據是于2008年10月在吉林省松花湖實驗站采集，實驗目的是利用均勻水平直線陣實現水下噪聲源近場高分辨定位與識別。實驗概況：實驗地點水深為35 m，陣元間距為0.75 m的8元聲壓水聽器構成的均勻水平陣放置于水面下15 m處，聲源放置于基陣正前方0.85 m處（即測量距離），預設聲源位置為（3，0），發射單頻連續信號，實驗數據處理結果如圖6、圖7所示。

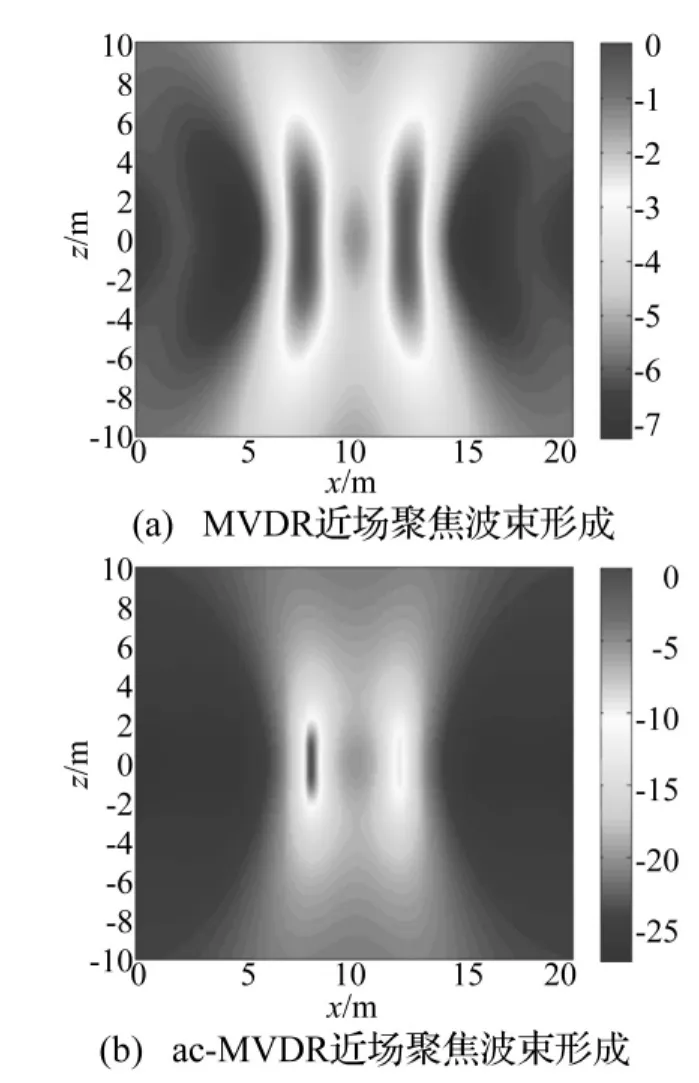
圖2 雙聲源仿真結果（f=160 Hz）Fig.2 Pairs of sound source simulation results（f=160 Hz）

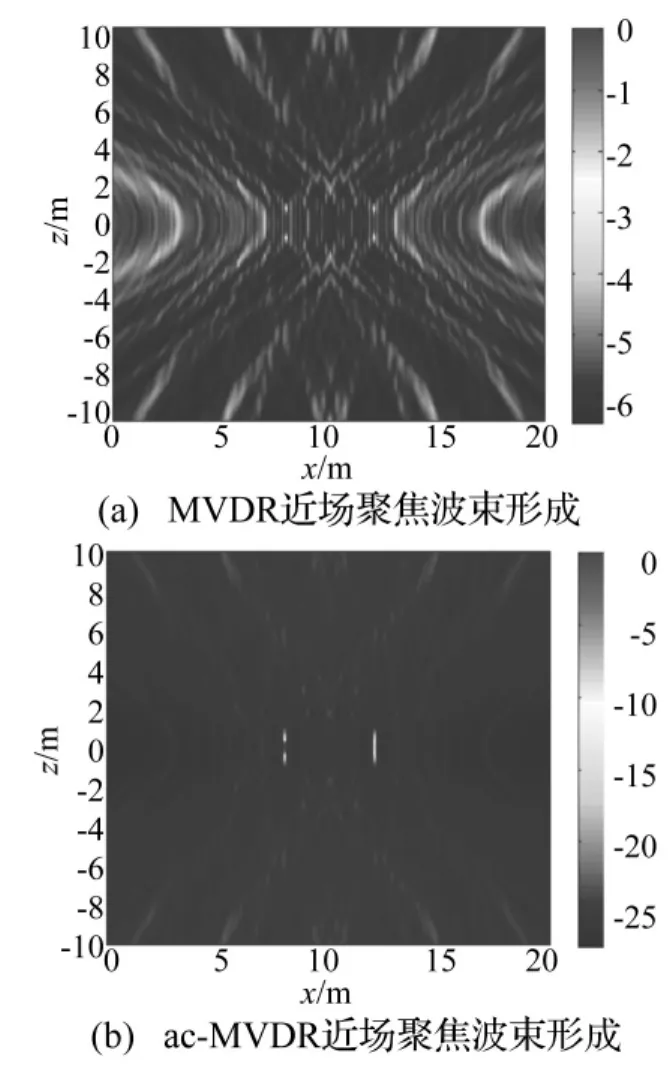
圖3 雙聲源仿真結果（f=4 kHz）Fig.3 Pairs of sound source simulation results（f=4 kHz）

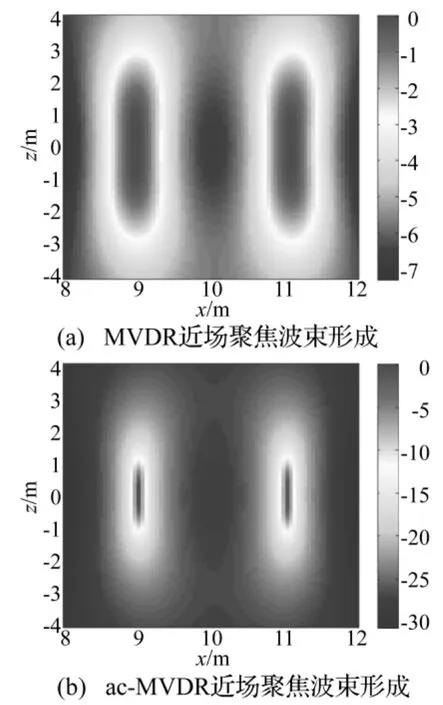
圖4 寬帶雙聲源幅度補償前后結果對比Fig.4 Broadband dual-source rate results compared before and after compensation

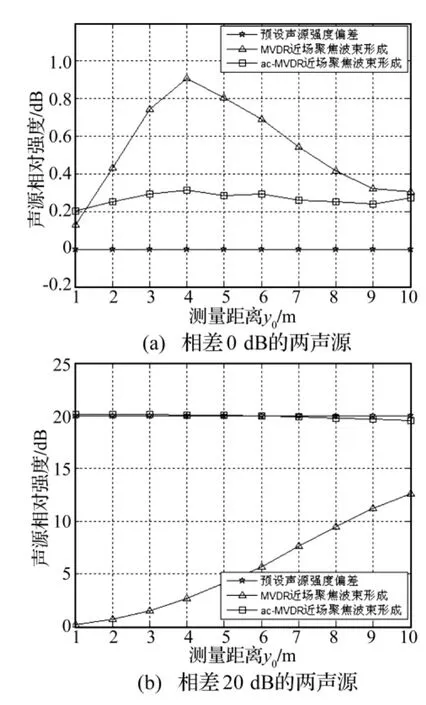
圖5 兩聲源相對強度估計Fig.5 Two sources estimate relative intensity

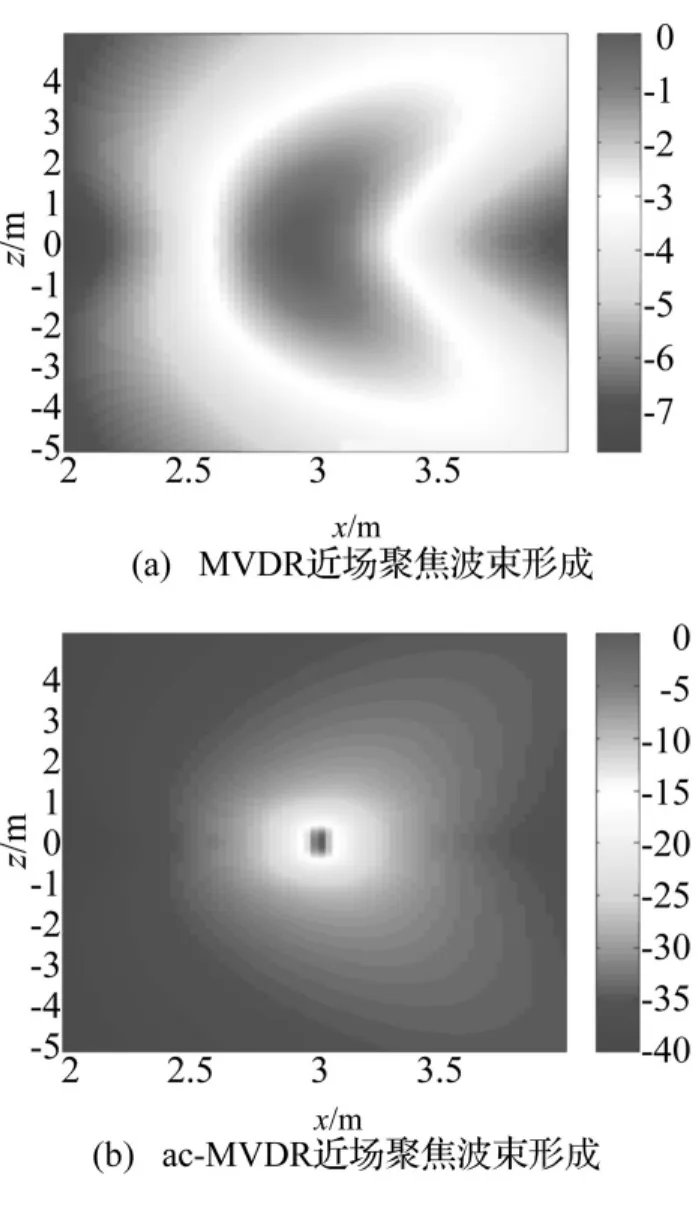
圖6 單聲源實驗數據處理結果（f=315 Hz）Fig.6 Single-source experimental data processing result（f=315 Hz）

圖7 單聲源實驗數據處理結果（f=4 kHz）Fig.7 Single-source experimental data processing result（f=4 kHz）

外場實驗數據處理結果驗證了基于幅度補償的MVDR近場聚焦波束形成的有效性。在實際情況下，MVDR近場聚焦波束形成在高頻段抑制空間混疊效果并不理想，但幅度補償后，可以有效的抑制空間混疊。由于測量距離較近，同時信噪比較高，使得本文方法在低頻段也能獲得很高的聚焦分辨率。

5 結論

本文介紹了基于幅度補償的MVDR水下噪聲源近場定位識別方法，并詳細分析了測量距離對該方法性能的影響，可以得到如下結論：

（1）通過幅度補償可以實現系統噪聲源相對強度估計，且估計偏差不大于0.5 dB。

（2）隨著測量距離的增加，本文方法會退化為MVDR近場聚焦波束形成。因此，為了保證在低頻段獲得相對理想的聚焦分辨率，應選擇合適的測量距離。

（3）在較高頻段，MVDR近場聚焦波束形成抑制空間混疊能力下降，但幅度補償后可以較好的抑制空間混疊。

（4）本文方法與MVDR近場聚焦波束形成相比并沒有增加計算負擔，算法簡單有效，計算量小，具有較強的工程應用價值。

［1］劉伯勝，雷家煜.水聲學原理［M］.哈爾濱：哈爾濱工程大學出版社，1997：224－236.

［2］Kook H，Moebs G B，Davies P，et al.An efficient procedure for visualizing the sound field radiated by vehicles during standardized passby tests［J］. JournalofSound and Vibration，2000，233（1）：137－156.

［3］雷 凌，單穎春，劉獻棟.行駛車輛噪聲源輻射研究進展及展望［J］.噪聲與振動控制，2006，26（4）：1－5.

［4］賈文強，陳 進，李加慶，等.波疊加聯合波束形成的局部聲場重建技術研究［J］.振動與沖擊，2010，29（1）：125－127.

［5］ Capon J.Proc. High-resolution frequency-wavenumber spectum analysis［J］.IEEE，1969，57：1408 －1418.

［6］ Wax M，Anu Y.IEEE Trans.on Signal Processing，1996，44（4）：928－937.

［7］時 潔，楊德森.基于MVDR聚焦波束形成輻射噪聲源近場定位方法［J］.大連海事學報，2008，34（3）：55 －58.

［8］薛山花，葉青華，黃海寧，等.利用近場MVDR雙聚焦波束成形方法實現被動測距［J］.應用聲學，2005，24（5）：177－181.

［9］楊德森，陳 歡，時勝國.基于MVDR算法的聲矢量陣水下噪聲源近場定位方法［C］.第十六屆信息論學術會議，473－477.

［10］時 潔，楊德森，時勝國.子帶分解MVDR高分辨寬帶近場聚焦波束形成算法研究［C］.2008年全國聲學學術會議論文集，2008.

［11］ Hung H，Kaveh M.Focusing matrices for coherent signalsubspace processing［J］.IEEE Trans.On ASSP，1988，36（8）：1272－1281.