基于EMD小波閾值去噪和時頻分析的齒輪故障模式識別與診斷

邵忍平，曹精明，李永龍

(西北工業大學 機電學院，西安 710072)

眾所周知，任何信號可表示為不同頻率的正弦波的迭加，經典的傅里葉分析能夠完美地描述正弦信號。但對于不連續的信號，如語言信號，就難以正確地予以描述。傳統的譜分析提供了平均的頻譜系數，這些系數只與頻率有關，而與時間無關。傳統譜分析要求所分析的隨機過程是平穩的，即過程的統計特性不隨時間的推移而改變。然而，許多隨機過程從本質上來講是非平穩的，例如記錄下來的語音或音樂的聲壓信號、振動中的沖擊響應信號、機組啟與停機信號等等。當然，非平穩信號的譜密度也可以用傳統的譜分析方法來計算，但是所得到的頻率分量是對信號歷程平均化的結果，并不能恰當地反映非平穩信號的特征［1］。

如果將非平穩過程視為由一系列短時平穩信號組成，任意一短時信號就可應用傅里葉變換進行分析。Gabor提出了窗口傅里葉變換概念，用一個在時間上可滑移的時窗來進行傅里葉變換，從而實現了在時間域和頻率域上都具有較好局部性的分析方法，這種方法稱為短時傅里葉變換(Short Time Fourier Transform，STFT)。近些年來，許多人已對短時傅里葉變換進行了大量的研究工作，如重慶大學的周丹［2］將短時傅里葉變換應用在脈象信號分析中的應用研究;Kuldip等［3］利用短時傅里葉變換對語言測試信號進行了識別;Debbal等［4］利用短時傅里葉變換研究了心跳信號 。齒輪傳動系統的信號是一種時變的非平穩信號，而當出現故障時這種非平穩信號特性更加的復雜，因此對故障特征信號進行時變的非平穩分析更加的適合，本文在試驗測試的基礎上，結合經驗模態分解的EMD小波閾值去噪對其系統的噪聲進行預處理，而后采用時頻分析的短時傅里葉分析方法對齒輪系統的齒根裂紋、分度圓裂紋、齒面磨損故障進行了特征提取與診斷，能夠較好地區分幾種典型故障。

1 去噪預處理原理

1.1 小波閾值去噪

在實際工程中，有用信號通常表現為低頻部分或是一些比較平穩的信號，而噪聲信號則通常表現為高頻信號。所以消噪過程可按如下方法進行處理:首先對信號進行小波分解，以門限閾值等形式對小波系數進行處理;然后對信號進行重構，即可以達到消噪的目的。一維信號消噪過程分為三個步驟［5］:① 選擇一個小波并確定一個小波分解的層次N，然后對信號進行N層分解;② 對從第1到第N層的每一層高頻系數，選擇一個閾值進行閾值量化處理;③ 根據小波分解的第N層低頻系數和經過量化處理后的第1層到第N層的高頻系數，進行一維信號的小波重構。

閾值選擇規則一般有以下幾種:

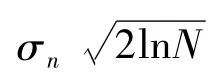
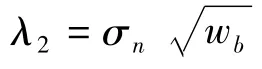
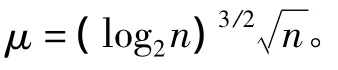
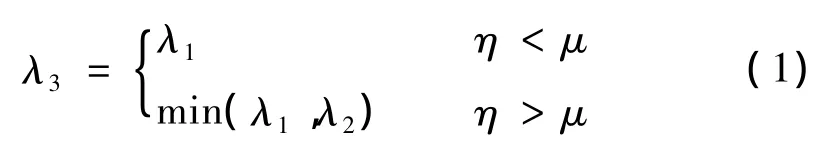
在實際應用中，由于小波閾值去噪的本身特性，這種規則還是會消除一些真實信號［6］。

本文采用閾值處理方法:

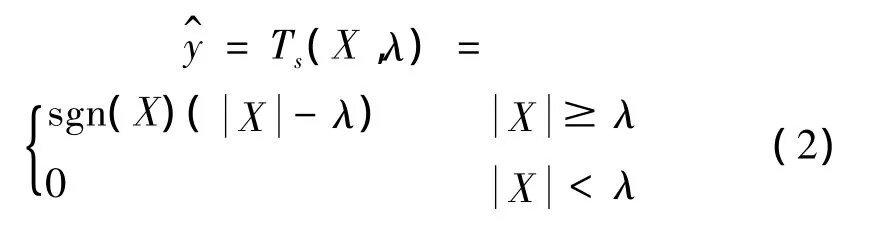
式中X為處理前的小波系數為處理后的小波系數，λ為閾值大小。從式(2)中可看出，幅值小于閾值λ的小波系數置為零，而高于該閾值的小波系數或完整保留、或作相應的“收縮”。最后利用處理過的小波系數進行逆小波變換，重構出新的有用信號。

1.2 基于經驗模態分解的小波閾值去噪

經驗模態分解方法有三大假設［7-8］:① 信號至少有一個極大值點和一個極小值點;② 特征時間尺度由極值點的時間推移定義;③ 如果整個信號只包含曲折點而不包括極值點，可以先微分一次或多次找到極值點，然后將所得到的分量進行積分以得到最后結果。這樣任何一個信號就可以被分解為有限個IMF(固有模態函數)之和，其中任何一個IMF都滿足以下條件:

(a)整個信號中，零點數和極值點數相等或至多相差1;(b)信號上任意一點，由局部極大值點確定的包絡線和由局部極小值點確定的包絡線的均值為零，即信號關于時間軸局部對稱。

經驗模態分解的具體步驟是:

(1)確定信號s(t)所有的極大值點和極小值點，然后將所有極大值點和所有極小值點分別用一條光滑的曲線連接起來，使兩條曲線間包含所有的信號。上下包絡線的平均值記為m1(t)，求出:

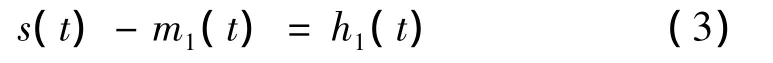
如果h1(t)是一個固有模態分量，那么h1(t)就是s(t)的第一個分量。

(2)一般情況下，h1(t)不滿足固有模態函數的條件，因此把h1(t)作為原始數據，重復步驟(1)，反復篩選k次，得到h1k(t)=h1(k-1)(t)-m1k(t)，使得h1k(t)變為一個IMF。記c1(t)=h1k(t)，則c1(t)為信號s(t)的第一個滿足固有模態函數條件的分量。

(3)c1(t)應該包含信號中最精細或者最短的分量，將c1(t)從s(t)中分離出來，得到:

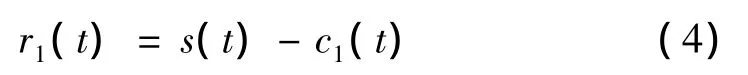
將r1(t)作為原始數據重復步驟(1)(2)，得到s(t)的第二個滿足固有模態函數條件的分量c2(t)，重復循環n次得到信號s(t)的n個固有模態分量。這樣就有:

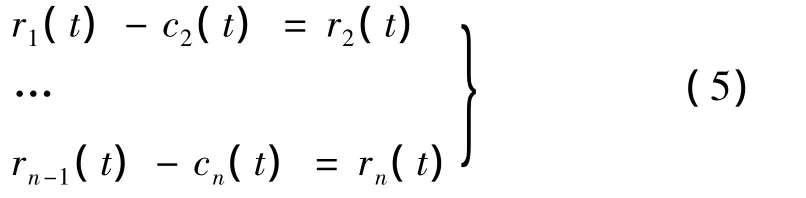
整個過程遇到如下任何一個準則即終止:① 當分量cn(t)或殘量rn(t)足夠小;② 當殘量rn(t)為一個單調函數不能再從中提取滿足固有模態分量時。這樣由式(4)和式(5)得到:

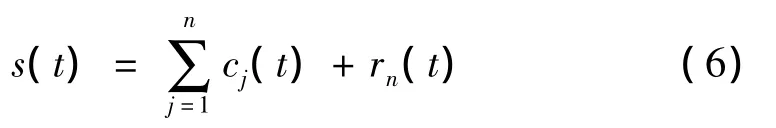
因此，可以把任何一個信號s(t)分解為n個固有模態分量和一個殘量rn(t)之和，分量c1(t)，c2(t)，…，cn(t)分別包含了信號從高到低不同頻率段的成分，且隨信號本身的變化而變化。通常，經驗模態分解方法分解出來的前幾個IMF分量集中了原信號中主要的信息。

由于直接小波閾值降噪方法的缺陷，本文將EMD與小波閾值降噪方法進行友好地結合進行消噪預處理。噪聲一般分布在信號的高頻部分，EMD通過篩選分解出的IMF分量恰好滿足從高頻到低頻的系列分布，如果將高頻IMF分量直接舍棄，重構原信號可達到降噪目的，但這樣會損失存在于高頻IMF分量中的有用信息。因此先對帶噪的高頻分量采用小波閾值降噪處理，獲得降噪后的數據，將其與不含噪聲的低頻IMF分量一起來重構原始信號，這樣以來，小波閾值降噪僅僅作用于高頻IMF分量，而不是直接作用于整個信號，這在很大程度上克服了小波閾值降噪的缺陷。

2 時頻分析理論

在分析非平穩信號時，時頻分析是一種很有效的方法，而短時傅里葉變換分布是其中最常用的時頻分布。對給定的非平穩信號s(t)，設h(t)是一個時間寬度很短的窗函數，它沿時間軸滑動，于是信號s(t)的短時傅里葉變換定義為:

式中，*表示復數共軛。實際上，正是窗函數h(t)的時移和頻移使短時傅里葉變換具有了局域特性，它既是時間的函數，又是頻率的函數。

實際上，S(t，w)是信號s(t)與窗函數h(t)的時移-頻移調制形式ht，w(τ)(基函數)的內積，

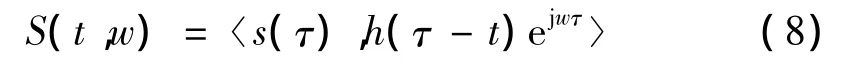
原則上，分析窗函數h(t)可以在平方可積空間內任意選擇。不過，在實際應用中，總是希望所選擇的窗函數是一個“窄的”時間函數，以使式(7)的積分僅受到s(t)及其附近值的影響。同樣，還希望h(t)的頻譜函數也是一個“窄的”函數。然而根據不確定原理，信號的時寬和帶寬不可能同時任意小。提出STFT的實際目的主要是了解信號的局域頻率特性，但窗函數的引入降低了局部的分辨力。對非平穩信號而言，其局部頻譜是時變的，過寬的窗函數會使相鄰的頻譜混淆，從而不能正確表現局部頻譜，即窗寬應與信號的局域平穩長度相適應［9-10］。

對式(7)兩邊取幅平方，則:

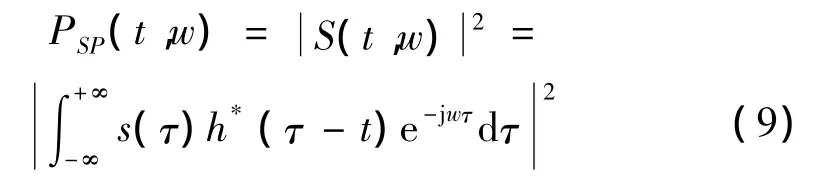
稱為S(t)的譜圖，或短時傅里葉譜，即原信號在t時刻的能量譜密度。顯然譜圖是恒正的，且是實的。

3 試驗裝置的建立與特征信號的獲取

齒輪系統試驗測試裝置如圖1所示。圖中由電動機驅動整個系統運轉，經過聯軸器后，將動力傳遞給減速器齒輪，經過減速器輸出后通過齒式聯軸器、轉矩轉速傳感器，將動力傳遞給磁粉加載器。試驗在齒輪上裝上加速度傳感器，并且傳感器安裝在齒輪故障的對稱位置附近。主動齒輪設置為故障齒輪，另外采用了傳輸環，通過它把隨齒輪一起轉動的加速度傳感器測得的信號無損的輸送出來。試驗時，通過控制柜觀察和控制轉矩與轉速的大小，以及通過磁粉加載器來對系統施加載荷。齒輪系統的運行狀態共分成四級轉速:300 r/min、900 r/min、1 200 r/min、1 500 r/min。主動輪上設置了六種故障，分別為齒根短裂紋故障、齒根長裂紋故障、分度圓短裂紋故障、分度圓長裂紋故障、齒面磨損故障和復合故障(齒根裂紋+齒面磨損故障)。在上述四種轉速下分別進行測試，采用了CRAS信號采集軟件系統進行信號采集、分析，運用上述的算法進行特征提取與診斷。

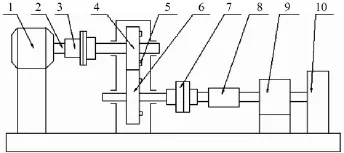
圖1 齒輪故障診斷測試試驗系統簡圖Fig.1 The testing equipment of fault gear system

4 齒輪故障識別與診斷

4.1 EMD小波閾值去噪處理

將EMD與小波閾值降噪結合起來進行消噪預處理。如圖2所示為300r/min裂紋信號EMD分解后的前6階IMF分量及其頻譜圖，從圖中可以看出，高頻分量IMF1的頻譜特征類似噪聲頻譜。如果將高頻IMF分量直接舍棄，重構原信號達到降噪目的，這樣會損失存在于高頻IMF分量中的有用信息。所以在此可先將對帶噪的高頻分量采用小波閾值降噪預處理，獲得降噪后的數據，將得到的數據再與不含噪聲的低頻IMF分量一起來重構原始信號，這樣小波閾值降噪僅僅作用于高頻IMF分量，而不是直接作用于整個信號，這在很大程度上改善了小波閾值降噪的缺陷。圖3(a)為300r/min裂紋信號經EMD分解后得到的高頻分量IMF1去噪后的結果，圖3(b)為重構后信號去噪后的結果。從圖中可看出，小波閾值去噪對高頻分量IMF1去噪的效果明顯，而從重構后的信號可以看出去噪后不僅保持了原有信號的特征，而且特征更加明顯，便于以后的分析處理。

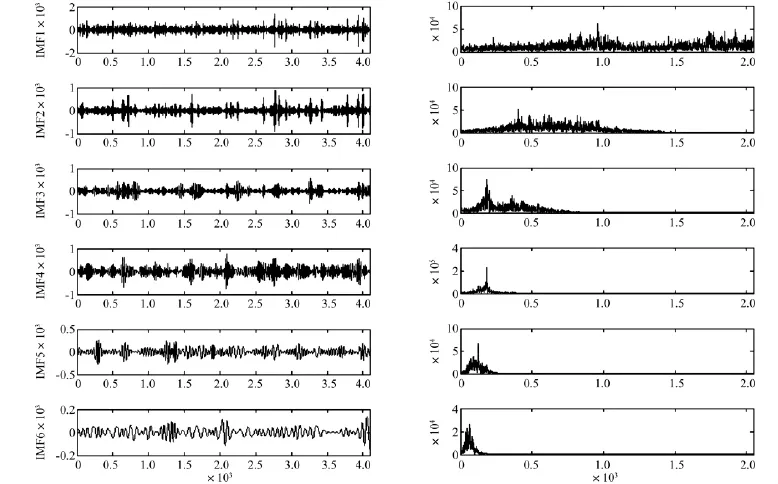
圖2 300 r/min狀態下裂紋信號EMD分解后的前6階IMF及其頻譜圖Fig.2 First 6-orders IMF and spectrum of EMD for cracked fault signal in 300r/min

由于隨機噪聲混雜在有用的特征信號中，經過EMD多層分解后出現了高低層區域頻段，而噪聲是處于高頻區域段的，這樣對測試數據采用工程上常用的方法進行評估其信噪比，設定一個閾值(一般為所有數據均方根的0.5倍)，分別對原始信號、小波閾值去噪后的信號以及結合EMD的小波閾值去噪的信號進行分析，將數據中高于或等于這個閾值的部分數據看成有用信號，而將數據中低于這個閾值的部分數據看成噪聲，這樣最終可估計出其信噪比，如表1所示。表1中給出了兩種轉速的運轉狀態下各種不同故障類型的信噪比模擬計算對比結果。從表1的對比結果可以看出，經過小波閾值去噪的信噪比要比原始信號的信噪比大，并且結合EMD的小波閾值去噪的信噪比要比直接采用小波閾值去噪的信噪比大很多。另外，以900 r/min系統運轉的齒根裂紋信號為例(如圖4)，并結合后面的時頻分析理論與頻率分析可知，說明了在時頻分析中基于EMD的小波閾值去噪相對于直接采用小波閾值去噪具有更加的優勢。從圖4(a)可以看出直接采用小波閾值去噪消去了一些有用信息，而圖4(b)顯示了經過基于EMD的小波閾值去噪，這部分有用信息得到了保留。

表1 各種情況下的信噪比Tab.1 The SNR for different fault in different running conditions

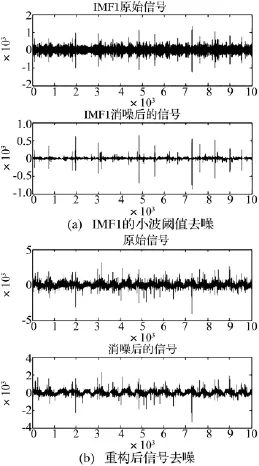
圖3 300 r/min裂紋信號的基于EMD的小波閾值去噪Fig.3 The result of wavelet de-noising by threshold using EMD for cracked fault signal in 300 r/min

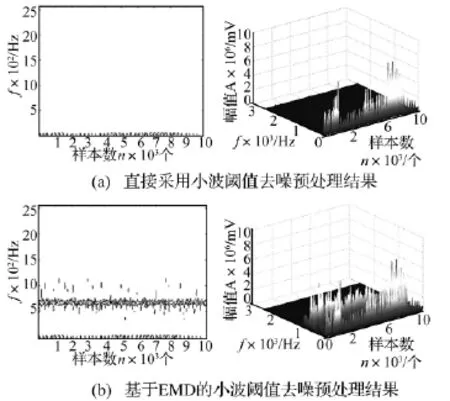
圖4 900 r/min齒根裂紋的信號短時傅里葉變換Fig.4 The result of Short Time Fourier Transform(STFT)for tooth root cracked signal in 900 r/min

4.2 時頻分析診斷與評價

首先通過對測試信號進行結合EMD的小波閾值去噪預處理，然后運用短時傅里葉變換對預處理過的信號進行分析處理，得出不同運轉狀態不同故障的有關圖譜，用于識別和診斷。在300 r/min狀態下，轉頻為5 Hz，齒輪的嚙合頻率為225 Hz。無故障情況的分析結果如圖5所示，可見無論從二維圖，還是三維圖，在0-10 Hz內有一個低頻(轉頻)存在，而且，230 Hz左右也存在一個能量很大的頻率(嚙合頻率)。同時，齒根裂紋分析結果如圖6所示，由于裂紋只發生在一個齒上，裂紋故障反映在轉頻上，因此，振動的能量主要集中在了轉頻上。分度圓裂紋分析結果如圖7所示，同理，低頻處的能量得到了加強，但由于裂紋位置的不同，分度圓裂紋信號在低頻的能量明顯比齒根裂紋信號的要大。齒面磨損分析結果如圖8所示，從圖中可見，能量布滿整個時頻平面，但是高頻得到了加強，這與齒根裂紋加強低頻的能量、齒面磨損加強高頻能量是吻合一致的。

在900 r/min狀態下，轉頻為15 Hz，齒輪的嚙合頻率為675 Hz。從圖4(b)、圖9、圖10中顯示可見，不論從二維圖，還是三維圖，都可以看出，只有670 Hz附近有很大的能量，這主要是齒輪的嚙合頻率，而在高速狀態下齒輪的嚙合效果下降，嚙合齒間沖擊增加［11］，反映在特征圖上就是嚙合頻率能量很強，而轉頻處的能量被淹沒了。齒根裂紋分析結果如圖4(b)所示，分度圓裂紋分析結果如圖9所示，從圖中可見，由于單齒裂紋故障反映在轉頻上，低頻的能量得到加強，另外還可看出分度圓裂紋信號在低頻的能量比齒根裂紋信號的要大，齒根裂紋信號的分布較為單一(分布范圍較小)，而分度圓裂紋信號的分布較為分散(分布范圍較大)，都有各自的特征。圖10顯示了齒面磨損信號的分析結果，可見能量布滿整個時頻平面，除了低頻處能量加強外，高頻處也得到了加強，這也是與齒根裂紋加強低頻的能量、齒面磨損除低頻加強外高頻能量也得到加強是一致的。值得注意的是，與300 r/min齒面磨損相比，高頻能量增加不大，而低頻能量明顯增強，這說明在高速狀態下，隨著磨損加劇，個別薄弱齒輪磨損故障有向其它故障形式發展的趨勢。

總之，同一轉速下，三種故障由于其能量分布的頻率及其幅值的不同，都有各自的特征，能夠得到有效的區分。不同轉速下，隨著轉速增加，能量在時頻圖上分布的頻率及其幅值都有些變化，并且都有增大的跡象，但依然能根據其能量分布特征區別出這三種故障。因此該方法能比較好的進行故障區分與診斷。

5 結論

通過將EMD與小波閾值降噪方法進行有效地結合，充分發揮二者的優點，使小波閾值降噪處理僅作用于高頻IMF分量，而不是直接作用于整個信號區域，這在很大程度上克服了直接采用小波閾值降噪方法的缺陷，提高了分析的精度，這樣更能突現出信號的故障特征。在消噪處理的基礎上通過與時頻分析方法的有機結合，能有效的識別不同種類的齒輪故障，如齒根裂紋，分度圓裂紋、齒面磨損等。該方法不僅適用于齒輪系統，而且可以推廣到其它故障識別與診斷領域。

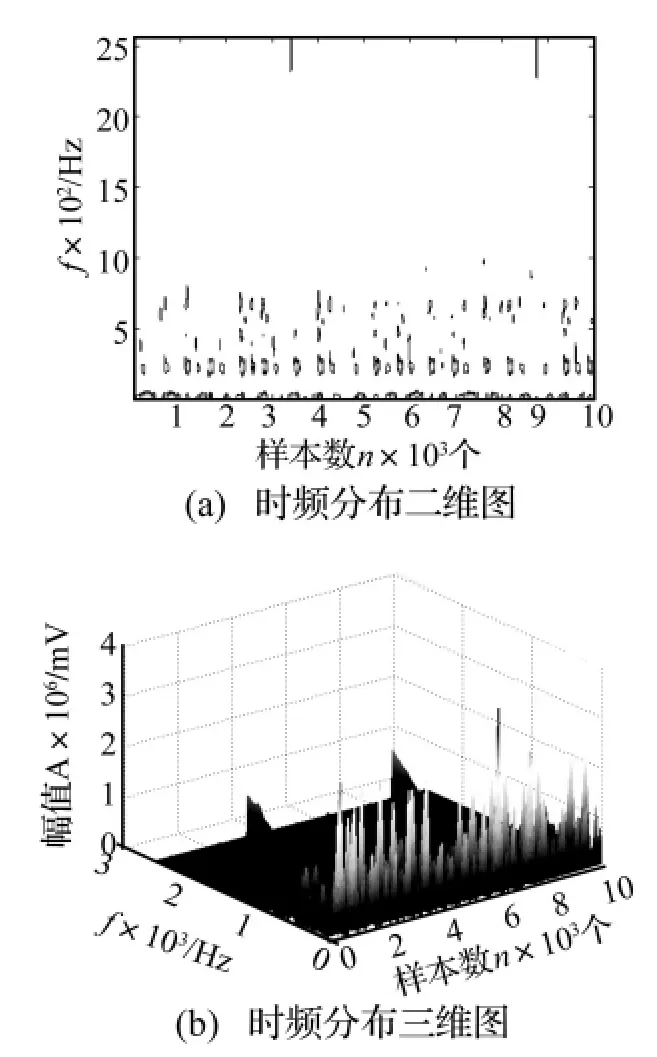
圖5 300 r/min狀態下無故障信號的時頻分析Fig.5 The result of Time-Frequency analysis for without fault signal in 300 r/min

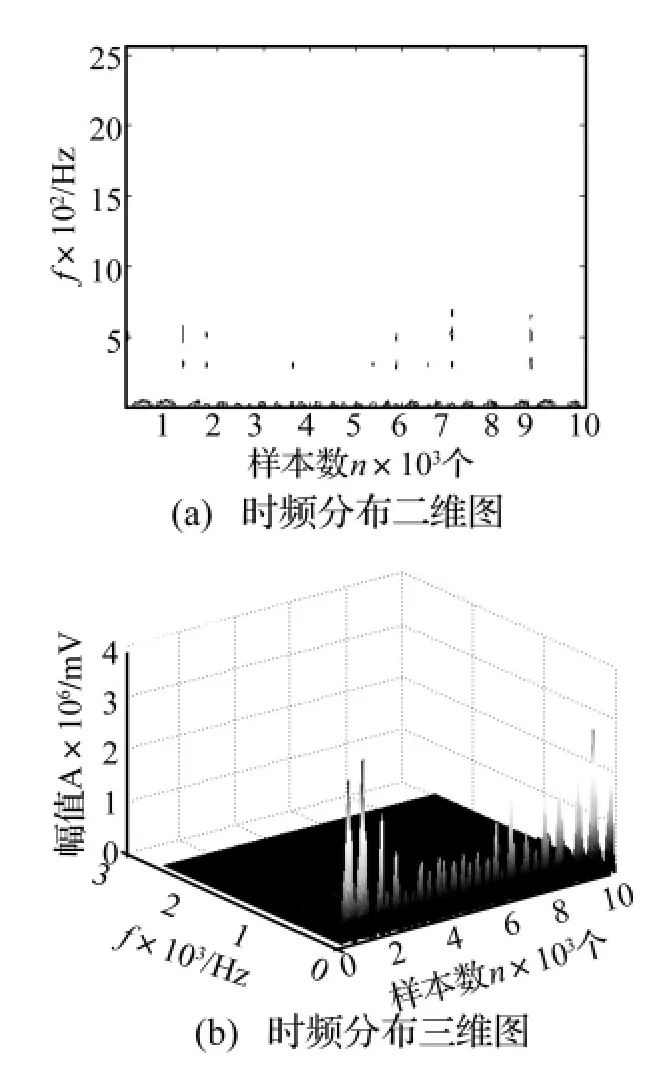
圖6 300 r/min狀態下齒根裂紋信號的時頻分析Fig.6 The result of Time-Frequency analysis for tooth root cracked signal in 300 r/min

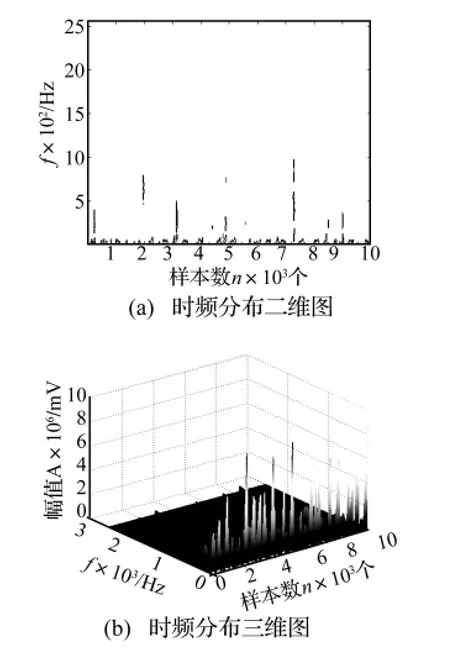
圖7 300 r/min狀態下分度圓裂紋信號的時頻分析Fig.7 The result of Time-Frequency analysis for pitch circle cracked signal in 300 r/min

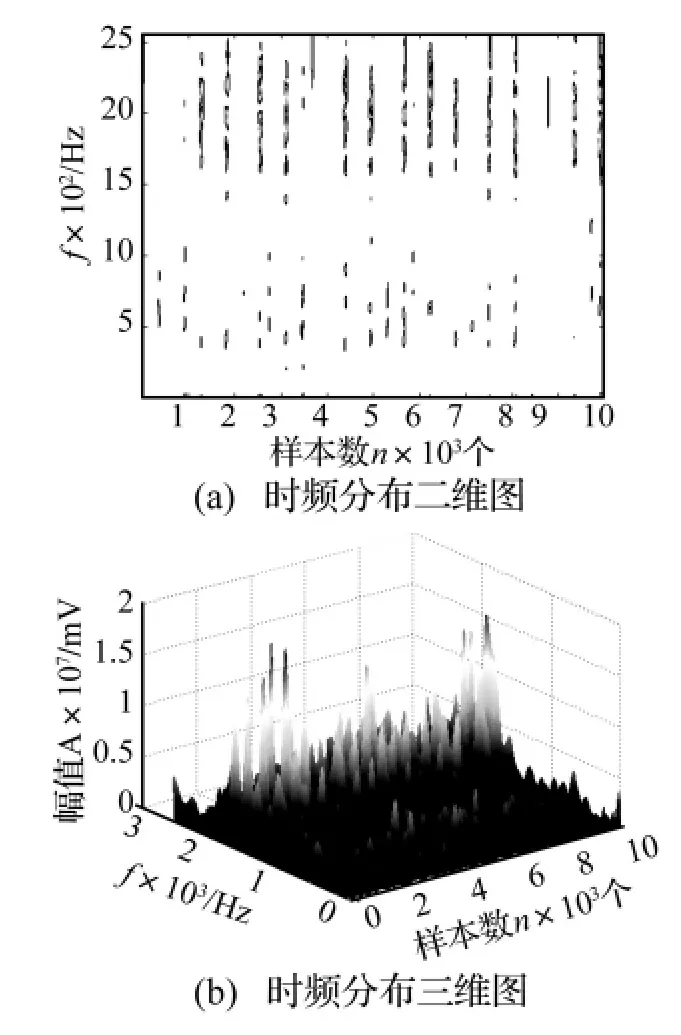
圖8 300 r/min狀態下齒面磨損信號的時頻分析Fig.8 The result of Time-Frequency analysis for tooth face abrasion signal in 300 r/min

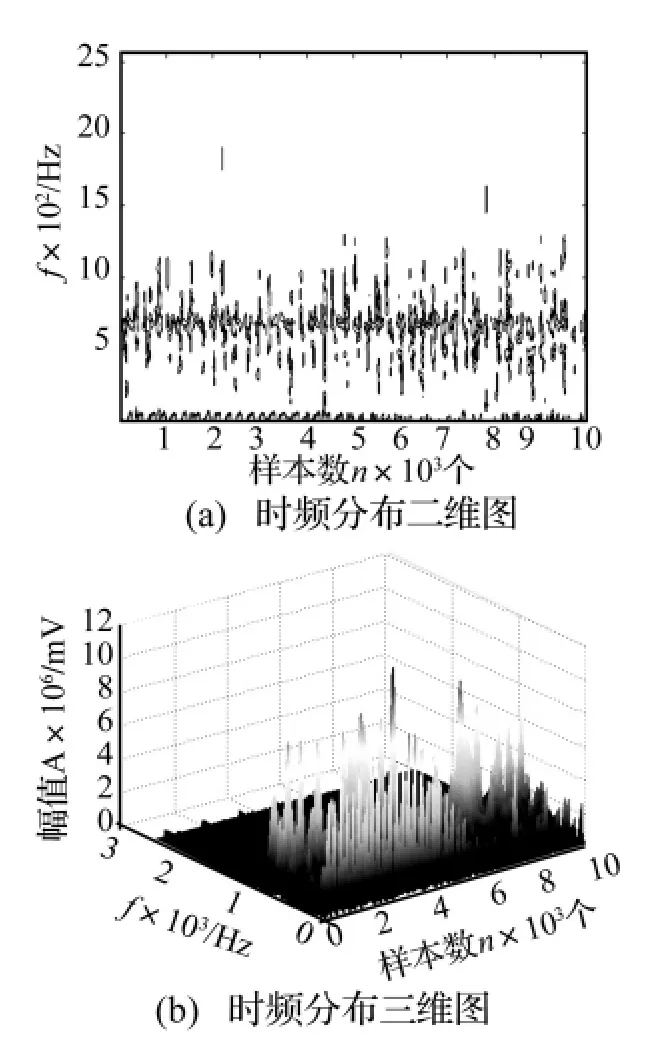
圖9 900 r/min狀態下分度圓裂紋信號的時頻分析Fig.9 The result of Time-Frequency analysis for pitch circle cracked signal in 900r/min

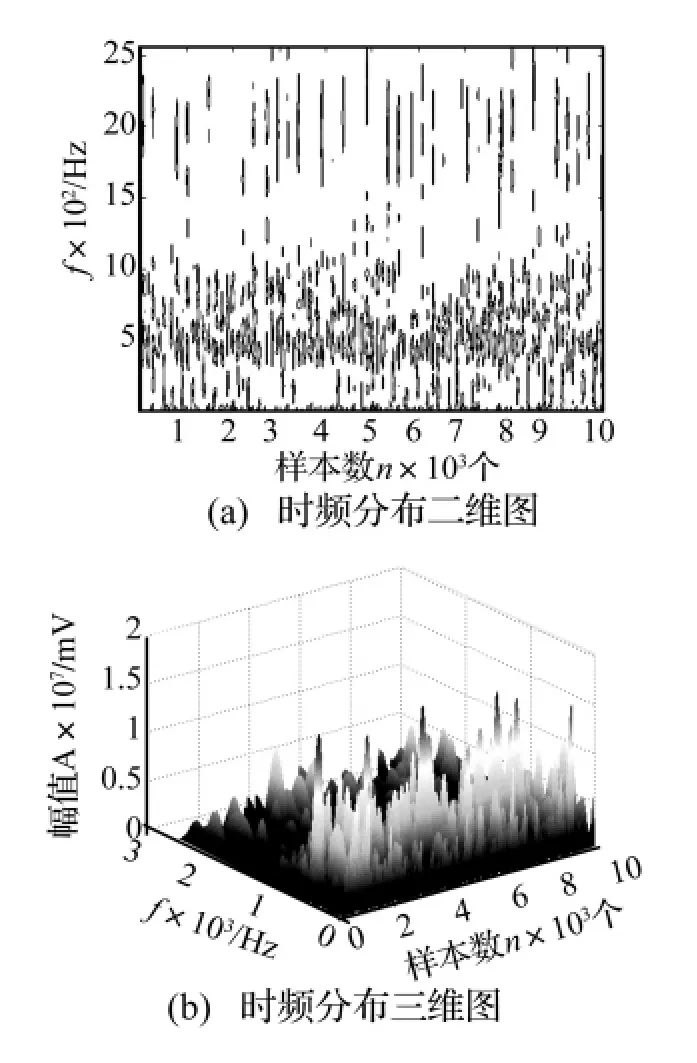
圖10 900 r/min狀態下齒面磨損信號的時頻分析Fig.10 The result of Time-Frequency analysis for tooth face abrasion signal in 900 r/min

［1］邵忍平，劉宏昱，徐永強，等.基于高階累積量的齒輪系統故障檢測與診斷［J］.機械工程學報，2008，44(6):161-168.

［2］周 丹.短時傅里葉變換和提升小波變換在脈象信號分析中的應用［D］.重慶:重慶大學，2008.

［3］Paliwal K K，Alsteris L D.On the usefulness of STFT phase spectrum in human listening tests［J］. Speech Communication，2005，45(2):153-170.

［4］Debbal S M，Bereksi R F.Time-frequency analysis of the first and the second heartbeat sounds［J］.Applied Mathematics and Computation，2007，184(2):1041-1052.

［5］ To A C，Moore J R，Glaser S D.Wavelet denoising techniques with applications to experimental geophysical data［J］.Signal Processing ，2009，89(2):144-160.

［6］李永龍.基于CI的智能診斷及其在機械傳動損傷檢測中的應用［D］.西安:西北工業大學，2010.

［7］鞠萍華，秦樹人，秦 毅，等.多分辨EMD方法與頻域平均在齒輪早期故障診斷中的研究［J］.振動與沖擊，2009，28(5):97-101.

［8］李振興，徐洪洲.基于經驗模態分解的小波閾值降噪方法研究［J］.計算機仿真，2009，26(9):325-328.

［9］ 秦樹人.工程信號處理［M］.北京:高等教育出版社，2008.

［10］ Belsak A，Flasker J.Detecting cracks in the tooth root of gears［J］，Engineering Failure Analysis，2007，14:1466-1475.

［11］ Chaari F，Fakhfakh T，Haddar M.Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness［J］.European Journal of Mechanics A-Solids，2009，28(3)，461-468.