基于Green函數的兩種STSF算法的比較

馬佳男，楊德森，時勝國，胡 博

(哈爾濱工程大學 水聲技術重點實驗室，哈爾濱 150001)

現有的基于Neumann邊界條件空間聲場變換的有限離散化算法主要采用了k-空間抽樣格林函數法對聲場進行重構，該算法直接對波數域下的格林函數進行抽樣，從而得到波數空間格林函數的離散陣列。該算法雖然簡單，工程上易于實現，但是由于Neumann邊界條件下k-空間振速-聲壓格林函數在輻射圓周上存在奇異性，這種奇異性會使得格林函數的幅值在輻射圓周上具有很大的躍變，從而影響重構精度。

1987年，Veronesi等人［1］首先提出實空間積分格林函數法，2004年，合肥大學的陳曉東［2］將該算法運用到了基于Dirichlet邊界條件下的聲壓場重構，獲得了很好的重構效果，并通過數值仿真證明該方法不僅適用于近場也同樣適用于遠場。隨著矢量水聽器的發展，可以通過測量質點振速來對聲場進行重構和預測［3-4］。由于介質質點振速方向與波達方向一致，所以振速提供了聲源方位的信息。在實際測量中更偏重于通過測量質點振速來重構聲場以獲得更好的重構精度和定位信息。

本文將實空間積分格林函數法運用到了Neumann邊界條件下基于法向質點振速測量的聲壓場重構中，推導獲得Neumann邊界條件下該有限離散化算法的計算參數，通過對其傅里葉變換后的角譜求逆得到聲壓-法向質點振速聲場重構時格林函數的角譜，并由數值仿真給出了該算法與k-空間抽樣格林函數法在聲場重構中基于不同重構參數的誤差分析，從而比較兩種格林函數法在聲場重構中的優劣。

1 Neumann邊界條件下的格林函數

理想流體介質中小振幅聲波傳播的波動方程［5］:

對于單頻聲波速度勢Φ=φe-jωt，ω為聲波的角頻率，φ是空間分布函數，它滿足Helmholtz方程:

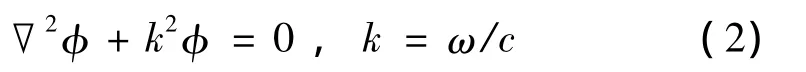
其中，c為聲速，k為聲波波數，故波數空間又稱為k-空間。通過Helmholtz方程，可以推導出Helmholtz公式。此公式用聲場邊界函數值表示聲場(穩態單頻波動聲場)的積分形式解。當點源都集中在某一封閉曲面s內時，Helmholtz公式表示為:

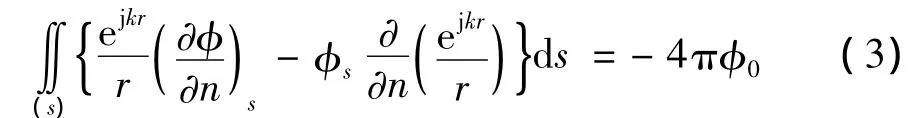
n為封閉曲面的外法線方向，φ0為Helmholtz方程的解析解。ejkr/r為所選的輔助函數，其中，r表示場點o到封閉曲面s的距離，此函數除在r=0點有奇點外，其它地方皆滿足假設條件和波動方程。

由式(3)可見，Helmholtz公式用φ和?φ/?n邊界值的面積分來確定聲場中任意一點的速度勢函數值，因此當已知邊界質點振速的分布和聲壓的分布值時，就可以用Helmholtz積分求出場中任意點的速度勢函數值。

格林函數表示一定邊界條件下點源的場，與邊界條件一一對應。單頻聲場中的格林函數滿足下面的方程［6］:

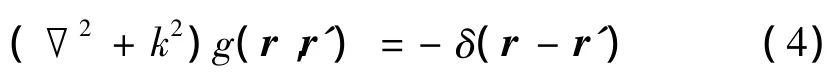
其中，r'代表聲源的位置，r代表場點的位置，δ函數表示點源，時間因子取 e-jωt，解得:

式(5)表示的是自由場中的格林函數，稱為格林函數的基本解。該式為具有1/r奇點形式的函數且滿足Helmholtz方程，可以成為式(3)的輔助函數。利用格林函數這種可選性可以選擇適當的格林函數形式來簡化Helmholtz公式。

Helmholtz方程與第二類邊界條件構成的定解問題叫做第二邊值問題或Neumann問題。對于式(3)，第二類邊界條件是指?φ/?n在區域邊界上為給定函數。相應地，該邊界條件下滿足式(5)和Neumann邊界條件的解稱為Neumann格林函數。

根據“虛源法”，平面邊界下格林函數的數學表達式為:

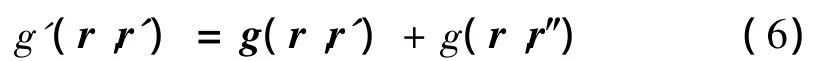
其中，r″表示虛源的位置。式(6)第二項對應著“虛源”，表示由平面邊界引起的反射波部分。在平面邊界絕對硬下，Helmholtz公式可以簡化成一項。由“虛源”和實際聲源的相位關系以及式(5)得到Neumann格林函數［7］:

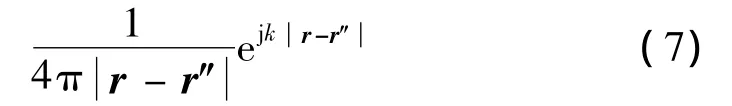
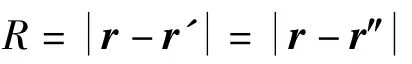
gN即為Neumann格林函數。由歐拉公式:

其中uz(x，y，z)，p(x，y，z)分別為空間點(x，y，z)處為法向質點振速、聲壓。

通過式(8)和式(9)可以得到Neumann邊界條件下，實空間域下法向質點振速-聲壓(簡稱為振速-聲壓)的格林函數，:

當?φ/?n=0時，對應為 Neumann邊界條件，此時對式(3)進行二維空間Fourier變換并利用歐拉公式，整理得到k-空間振速-聲壓的格林函數:

以及k-空間聲壓-法向質點振速的格林函數:

其中:

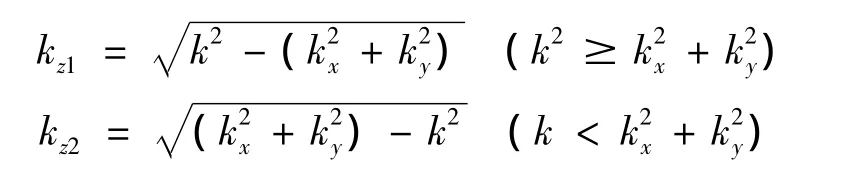
2 實空間積分格林函數法

本文應用的實空間積分格林函數法是對已經離散化的實空間格林函數各子塊的中點(x0，y0)處進行二元泰勒級數的展開，通過取不同階數的泰勒展開來近似連續光滑實空間格林函數在子塊上的積分值，即式(10)的積分值［8］。本文參考文獻［3］，修正了文獻［1］給出的計算參數，利用取泰勒展開式的前4階得到實空間積分格林函數的近似結果。

首先，令全息孔徑為Lx×Ly，將全息面離散為N×N矩陣，其中每個子塊的大小為 Δx×Δy，其中 Δx=Lx/N，Δy=Ly/N，于是有實空間格林函數的離散表達式:

其中，m1，m2分別代表x，y方向上離散格林函數的子塊序號，于是各子塊中心坐標x0=m1Δx，y0=m2Δy，dz為重建面與全息面間的距離，這里簡稱為重構距離。

對式(13)的各子塊中心做4階泰勒展開，通過整理得到的數學表達式為:

上式給出的系數ai，是通過泰勒四階展開得到的格林函數展開系數:

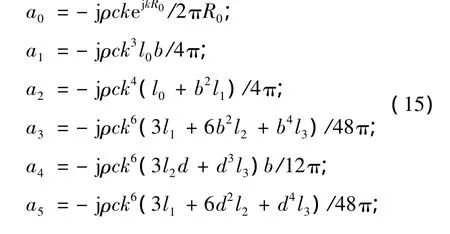
上式b=kx0，d=ky0。令a=kR0，

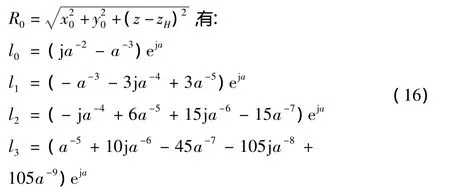
式(14)是非中心子塊4階泰勒展開的結果，當x0=0，y0=0且dz→0時R0→0，這時格林函數按照上式的計算方法具有奇異性，不能進行直接的近似，所以在計算中心子塊積分值時將該子塊分成兩部分，即圓形區域和四個角區域。

于是，帶入式(10)所得圓形區域的積分可用極坐標表示為:

然后，討論正方形中剩余的4個角域上的積分，因為格林函數的對稱性，所以這4個積分相同，只需求出其中一個即可，于是有:

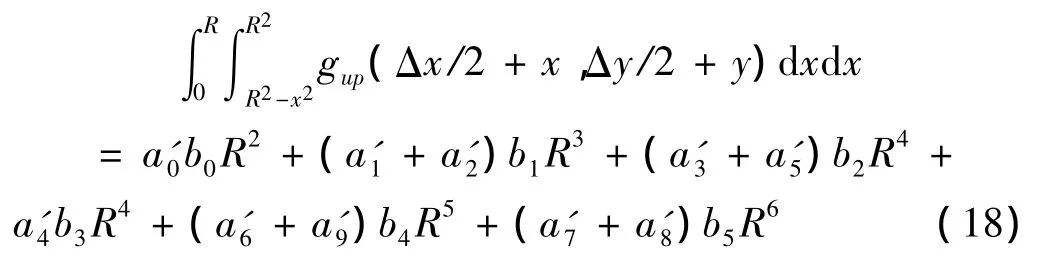
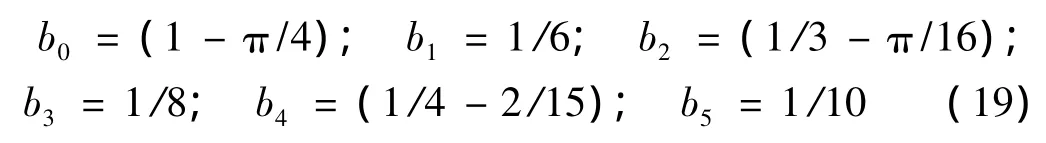
將中心子塊的格林函數與非中心子塊格林函數相加，就得到了基于法向質點振速測量Neumann邊界條件下的實空間積分格林函數。

令采樣點數N=64，測量孔徑為4 m×4 m，聲速c=1 500 m/s，對比在不同重構距離下，k-空間抽樣格林函數與實空間積分振速-聲壓格林函數的幅值分別在k空間和實空間域上的分布特點:

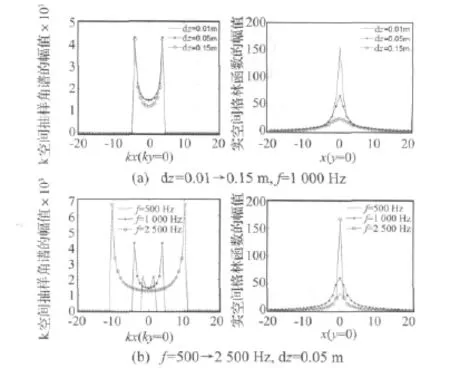
圖1 兩種算法下振速-聲壓格林函數幅值分布圖Fig.1 The amplitude distribution of the two algorithms in the vibration velocity reconstructing the sound pressure

由圖1可以看出:

(1)振速-聲壓實空間積分格林函數在頻率和全息孔徑不變的條件下，隨著重構距離的減小，其幅值變得尖銳，且孔徑中心與邊緣的幅值衰減急劇增加;而當重構距離保持不變時，該格林函數幅值隨著頻率的增加而變得陡峭;以上分布特點說明當重構距離小于0.05m或頻率增大時，由于實空間積分格林函數曲線的面積僅限于x=y=0附近很窄的范圍內，從而導致該區域下采樣點數較少，從而影響重構精度。

(2)k-空間抽樣格林函數在輻射圓周上有躍變，隨著重構距離的增大，輻射圓周上的躍變變得愈發尖銳;同時，聲源頻率的增加同樣可以加劇輻射圓周上的躍變。這種躍變會使重構面孔徑邊緣處的函數具有奇異性，增大重構誤差，所以由此可以推斷該算法下的格林函數對重構距離和聲源頻率比較敏感，在對聲場進行重構時會產生較大誤差。

3 數值仿真分析

3.1 振速－聲壓的聲場重構

下面利用實空間積分格林函數法和k-空間抽樣格林函數法分別進行振速-聲壓的聲場重構。取與圖1相同的仿真條件，f=1 000 Hz，zH為全息面與聲源間的距離。

圖2 兩種算法基于法向質點振速測量的聲壓場重構Fig.2 The two algorithms reconstructing the sound pressure field based on measuring normal particle vibration velocity

圖2給出的是兩種算法下，法向質點振速重構聲壓場的等高線圖。從圖中可以看出:

(1)基于實空間積分算法的聲壓場重構，雖邊緣有起伏，但該算法下得到的聲壓幅值具有良好的衰減特性。而當dz和zH增大后，起伏也隨之增大，由于NAH應用的條件之一是聲壓幅值在全息面邊緣上具有足夠大的衰減，因此誤差大的這些點對整個聲場的空間變換影響很小，而影響大的區域在孔徑中心，只要將該區域的幅值誤差控制在一定的范圍內，就能最終保證重構精度。

(2)k-空間抽樣格林函數法在孔徑邊緣不僅波動較大，且在dz、zH很小的情況下，“卷繞誤差”使孔徑邊緣產生了虛源;隨著dz和zH的增大，虛源強度增大從而影響對聲源特性的識別。即使利用漢寧窗和k域濾波，都不能抑制卷繞誤差對重構結果的影響。

從式(9)可以看到，當聲源頻率為聲速的整數倍時，k-空間格林函數的分子為零，存在奇異性，不能通過k-空間抽樣格林函數法對聲場進行重構。所以我們重點考察聲源頻率對實積分格林函數法和聲壓場重構精度的影響。令dz=0.01 m，zH=0.1 m。

由圖(3)可以看出，實積分格林函數在低頻條件下重構聲壓幅值具有較好的收斂性和衰減性;在高頻條件下，重構聲壓幅值衰減率減小，且孔徑邊緣有起伏，重構誤差增大。

圖3 不同聲源頻率下實積分格林函數法的重構聲壓場Fig.3 Using the real integral Green algorithm to reconstruct the sound field with different frequencies

3.2 聲壓－法向質點振速的聲場重構

將經過FFT變換得到實空間積分法向質點振速-聲壓格林函數的角譜求逆，就可以得到Neumann邊界條件下，聲壓-法向質點振速格林函數的角譜，通過該譜函數對法向質點振速進行聲場重構。

下面利用實空間積分格林函數法和k-空間抽樣格林函數法分別對基于聲壓測量的聲場進行聲壓-振速的聲場重構。取與圖2相同的仿真條件，令dz=0.02 m，zH=0.15 m。

圖4 兩種算法基于聲壓測量的法向質點振速場重構Fig.4 The two algorithms reconstructing normal particle vibration velocity field based on measuring the sound pressure

從圖4可以看出相對于聲壓的幅值分布，法向質點振速的幅值函數的收斂性更好，在孔徑中心較為尖銳。所以為了更好地比較兩種算法，圖4給出的是兩種算法的剖面圖。在k域濾波參數相同的條件下，實空間積分格林函數法孔徑邊緣波動較小，而k-空間抽樣格林函數法孔徑邊緣的波動較大。為了更直觀地對比兩種算法的優劣，利用下式計算重構聲場的累積誤差:

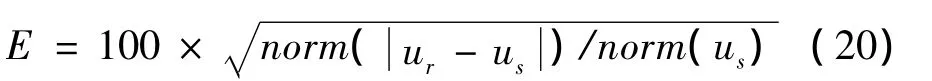
圖5分別給出了兩種算法下，不同的聲源頻率、重構距離、全息面距離重構聲場的幅值誤差變化曲線。其中:圖5(a)中zH=0.15 m，dz=0.02 m;圖5(b)中 dz保持0.02 m 不變;圖 5(c)中zH=0.15 m。

可以看出:① 相對于k-空間抽樣算法，實空間積分算法不僅可以得到較高的重構精度，而且各重構參數的累積誤差隨著參數的變化相對穩定，說明該算法具有較強的適用性;② 圖5(c)虛線表示當dz＞0.04 m時，k-空間抽樣算法對法向質點振速場重構失敗，因為孔徑邊緣的幅值出現的指數型增長已經無法對聲源做出精確的識別。雖然由實空間積分格林函數在dz＞0.05 m處得到的累積誤差很大，但是其誤差主要集中在孔徑中心，孔徑邊緣處的誤差很小，幾乎不影響對聲源特性的判斷。

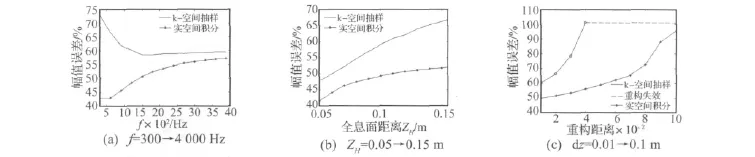
圖5 不同重構參數對重構精度的影響Fig.5 Different reconstruction parameters on the reconstruction accuracy

4 結論

通過數值仿真結果可以得出如下結論:

(1)當通過測量法向質點振速對聲壓場進行重構時，相對于k-空間抽樣法，實積分格林函數法有效地抑制了重構中常存在的“卷繞誤差”，且該算法對聲源頻率不如k-空間抽樣格林函數敏感，雖然在高頻條件下，孔徑邊緣有波動，但沒有出現較大的誤差，對識別聲源的影響較小。說明在基于空間聲場變換的全息重構中，由實空間積分得到的格林函數的角譜更理想并更好地改善了法向質點振速-聲壓k空間格林函數在輻射圓周上的奇異性。

(2)振速-聲壓法向質點振速進行聲場重構時，實空間積分格林函數法有效抑制了由于逆向重構產生的“吉布斯”效應，且各重構參數的累積誤差隨著參數的變化相對穩定，累積誤差相對較小。

(3)通過對比和分析，Neumann邊界條件下的實空間積分格林函數法相對于k-空間抽樣格林函數法具有更好的重建精度，更有效的識別聲源，而其應用特點也可為進一步的工程實踐提供參考。

［1］ Veronesi W A，Maynard J D.Nearfield acoustic holography(NAH)II.Holographic reconstruction algorithms and computer implementation［J］.J.Acoust.Soc.Am.，1987，81(5):1307-1322.

［2］陳曉東.近場平面聲全息的測量和重構誤差研究［D］.合肥:合肥工業大學，2004.

［3］張永斌，畢傳興，陳 劍，等.基于質點振速測量的近場聲全息技術［J］.農業機械學報，2007，38(9):112-116.

［4］ Jacobsen F，Liu Y.Near field acoustic holography with particle velocity transducers［J］.J.Acoust.Soc.Am.，2005，118(5):3139-3144.

［5］何祚鏞，趙玉芳.聲學理論基礎［M］.北京:國防工業出版社，1981.

［6］梁昆淼.數學物理方法［M］.北京:高等教育出版社，1995.

［7］ Veronesi W A，Maynard J D.Digital holographic reconstruction of source with arbitrarily shaped surfaces［J］.J.Acoust..Soc.Am.，1989，85(2):588-598.

［8］ Wu S F.Methods for reconstructing acoustic quantities based on acoustic pressure measurements［J］.J.Acoust.Soc.Am.，2008，124(5):2680-2697.