法向接觸剛度對裝配體振動模態影響的研究

艾延廷，翟 學，王 志，喬永利

(沈陽航空航天大學 遼寧省數字化工藝仿真與試驗技術重點實驗室，沈陽 110136)

在工程領域，結構分析的研究對象往往是由眾多零件、組件和部件經過裝配而形成的機械系統。工程結構裝配形式繁多，包括配合連接、螺栓連接、銷連接、焊接、膠結、嚙合連接等。在對裝配體進行模態仿真和動力學分析時，由于結合面處理的技術問題，不得不對分析模型進行簡化。如不考慮零件之間的連接配合關系，而是將裝配體中的各個零件直接合并為一個整體，認為裝配件之間是剛性連接。由于有預載荷的機械裝配體(如螺栓法蘭連接)的接觸表面存在接觸應力，不同的接觸應力和接觸面粗糙度，使接觸面間形成分布不均勻的法向接觸剛度，會對整個裝配體的振動模態產生影響。剛性連結假設不能正確反映裝配結構間的連接剛度和阻尼，其動力學特性計算結果往往與實際情況相差很大，無法實際應用。本文的研究起源于對航空發動機盤式拉桿轉子各輪盤之間以及盤軸間的連接剛度對發動機轉子的軸向和橫向振動模態影響的分析。該方面的研究主要方法有兩種，一是模態實驗［1］，二是對部件做集中參數處理后通過鍵合圖法［2-3］或有限元法［4-5］進行數值計算。隨著發動機轉子以及整機結構設計技術的發展，要求在設計初期即進行轉子和整機的有限元建模，進而通過仿真實現其動力學優化設計。文獻［1］提出的方法是對設計并加工出的實物模型進行實驗模態分析，因而無法在設計之初進行模態計算與分析;文獻［2-3］使用的鍵合圖法與輪盤等結構的有限元模型無法聯合使用。文獻［4］采用有限元法中的接觸單元進行接觸剛度分析與模態計算。在一個裝配體中，常常有多處采用螺栓聯接結構，如在某型航空發動機轉子兩級盤-盤聯接中有50余螺栓，如果對每個螺栓都進行有限元建模，則需要大量的計算機資源，造成大量的時間消耗，甚至計算機無法運行，因此，該方法的實際應用受到限制。文獻［5］通過對傳統的有限元方法進行改進，并編程計算，實現接觸面接觸剛度對轉子動力特性影響的研究與分析。本文試圖對帶有預緊力的螺栓聯接結構的接觸剛度進行有限元等效計算，以便為工程中的螺栓聯接有限元建模與仿真問題提供一個有效方法。

本文在靜態接觸分析的基礎上，依據接觸力學相關理論，根據接觸面的粗糙度參數確定出接觸剛度［6-7］;然后在有限元模型中加入實體層單元，通過改變實體層單元的彈性模量來等效接觸剛度;最后再通過有限元方法對裝配體進行模態分析。

1 接觸剛度理論

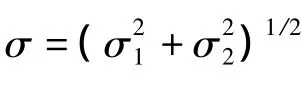
取表面的平均水平線為基準線，稱剛性表面到基準距離為間隔d，稱頂點到基準的距離為頂點高度zs。zs的平均值為，其概率密度函數為φ(zs)。如果在名義表面積A0中有N個頂點，則在間隔d處接觸的頂點數為:

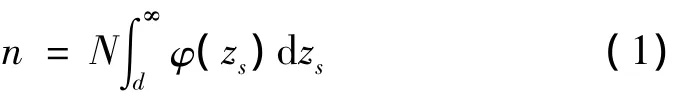
如果頂點高度超出了間隔，那么它將被壓縮δ=zs-d，并且將在半徑為a的小圓形區域中與平面構成接觸。因此，第i個頂點具有的接觸區域為:

壓縮該頂點所需要的力可寫成:

式中f(δ)和g(δ)與接觸表面的材料性質有關。如果變形完全是在彈性極限之內，由Hertz方程有:

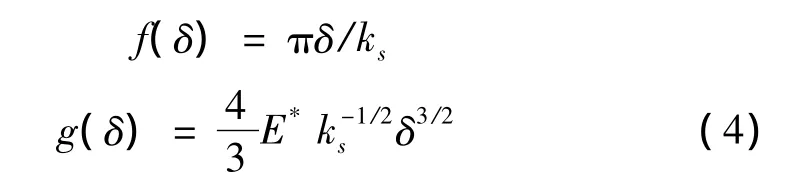
為了求出真實的總接觸面積A和總的名義應力=P/A0，必須對高度超出間隔的所有凹凸起伏求和。于是有:

將式(4)代入式(5)，并進行歸一化處理可得:

由式(6)可得接觸剛度kc:

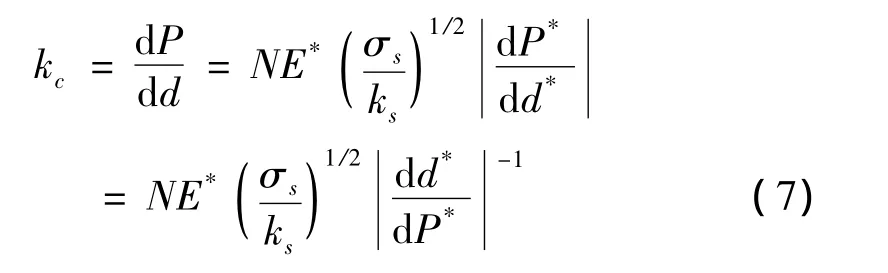
2 模型建立

2.1 接觸剛度計算

許多實際的表面，特別是未處理過的基表面，其高度分布服從Gauss分布。對于標準偏差為σ的Gauss分布，頂點高度的分布非常接近Gauss分布，其標準偏差σs≈σ，頂點的高度位于表面的平均水平之上0.5σ～1.5σ之間;頂點曲率與該表面的均方根曲率量級相同，即=σk;如果波狀表面是隨機的各向同性表面，采用趨近于零的抽樣間隔，則單位面積的頂點數為ηs=1.209，其中ηp為跡線單位長度上的峰點數，通過分析輪廓跡線中的峰點數確定。均值為zs，方差為σs的Gauss分布的概率密度函數為:

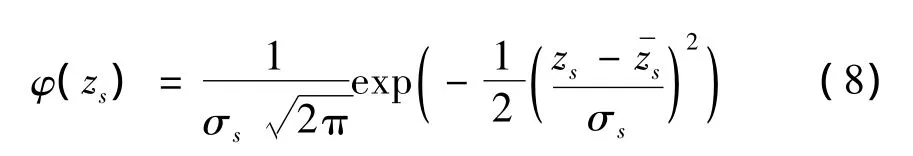
由式(6)和式(7)可得:

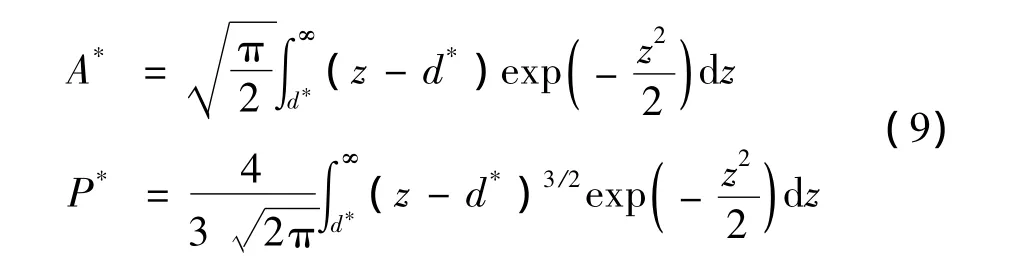
基于式(9)得到真實接觸面積和歸一化間隔隨無量綱載荷的變化關系如圖1所示。

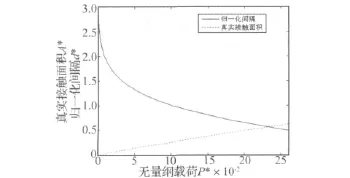
圖1 真實接觸面積和歸一化間隔隨無量綱載荷的變化Fig.1 The variation of real contact area and normal step as a function of dimensionless load

根據式(7)和圖1，可以確定接觸剛度。

上面接觸剛度理論是基于假設每一個凹凸的變形與其相鄰的凹凸無關。當實際接觸面積與名義接觸面積相比不再很小時，例如在歸一化間隔小于0.5的地方，誤差將加大。在另一端，如果歸一化間隔大約超過3.0時，則使用統計方法來研究接觸問題變得不精確。

2.2 有限元等效剛度建立

通用有限元計算軟件能夠對接觸問題進行靜力學分析，但是這些分析假定了接觸面連續，對于包含粗糙度的接觸面不能夠進行分析。本文利用通用有限元軟件計算出接觸表面的接觸壓力;然后使用這些接觸壓力數據和接觸表面的粗糙度以及接觸部件的材料屬性，根據接觸力學的知識計算出接觸表面每個單元的接觸剛度;然后使用層單元，將接觸剛度折算為層單元的彈性模量來修改模型。

折算的具體過程如圖2所示。當具有名義面積A0的接觸單元和下面的目標單元接觸時。該法向接觸剛度可等效為層單元的剛度，如圖2所示。建模時比較方便的做法是將原來靠在一起的接觸單元和目標單元移開一定距離h，可以取接觸時的最大間隔值。等效公式為:

通過調節單元的彈性模量E'就可以等效接觸剛度kc了。

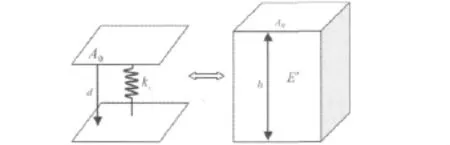
圖2 使用層單元來模擬接觸剛度Fig.2 Contact stiffness simulated with solid elements

由于不考慮切向接觸剛度，材料的密度和泊松比都可以看做為0。接觸面用層單元模擬，接觸面的剛度用層單元彈性模量等效，層單元的厚度為h，層單元兩端與原來實體的連結采用Nastran軟件中的多點約束技術完成。

3 算例

3.1 接觸剛度計算

本文研究的物理模型長l=10 mm，寬b=10 mm，截面面積A=100 mm2，高h=50 mm。材料參數為:彈性模量E=2.1e11 Pa，泊松比 μ =0.3，密度 ρ=7 850 kg/m3。接觸面取在立方體的中間位置。立方體的下端面支撐在剛性水平面上，立方體的上端面施加壓強108 Pa。

中間接觸面的間隔即層單元的厚度h取1 mm。文獻［4，7］使用靜態實驗和模態實驗，并通過參數識別對類似結構的法向和切向接觸剛度進行了測量。

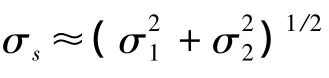
3.2 基于解析解的模型固有頻率計算

接觸面間的接觸剛度可以通過接觸面間的接觸參數的實驗測量及其分布特征分析按上述公式計算。而接觸剛度一旦確定，即可按層單元法和多點約束技術進行有限元分析與計算。計算的準確性，一般采用實驗的方法對最終的模態分析結果進行驗證，實際包含對接觸剛度計算的準確性和有限元模型的準確性兩方面的驗證。本文假設接觸剛度計算是準確的，只進行有限元模型的正確性驗證。研究兩個長立方體，其中間接觸，接觸剛度用彈性系數為kn的彈簧模擬，研究其縱向振動問題，建立圖3所示力學模型。

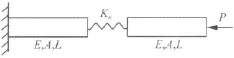
圖3 計算的力學模型Fig.3 Mechanical model for calculation

根據有關知識，可以推導出:

或:

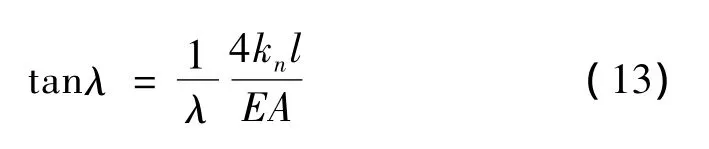
由式(13)，可以求出各階固有頻率的解析解。

3.3 基于有限元等效的振動模態計算

本文只分析結構在豎直方向的振動，所有節點水平方向約束。圖4中的h取為1 mm。由式(10)計算出等效實體單元的彈性模量為E'=1.04×1010N/m2，這比上下立方體的材料的彈性模量要小，所以其固有頻率比由上下立方體所構成的整體部件要低。表1列出了考慮法向接觸剛度的等效模型解、整體有限元模型解與固有頻率的解析解對比，可以看出，有限元等效模型解與解析解非常接近，而不考慮接觸問題的整體模型解較有限元模型解誤差大。

圖5給出了二者前3階振型的對比，不同的顏色代表不同的位移量，如在第一階振型圖中，顏色從藍到紅，對應振動位移從0到最大值1。由圖5可以看出，等效模型與整體模型二者在振型上也存在差異。

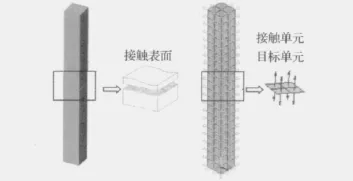
圖4 物理模型(左)、有限元接觸模型(右)Fig.4 Physical model(left)，element contact model(right)

表1 考慮法向接觸剛度的等效模型、整體有限元模型與固有頻率解析解對比(Hz)Tab.1 Contrast of the frequencies for the equivalent model considering contact stiffness，the solid model and theoretical solution(Hz)

圖5 等效模型(右)同整體模型(左)的前3階模態振型對比Fig.5 Comparisons of the first three vibration models for the equivalent model(right)and solid model(left)

4 結論

本文探討了在接觸面間添加一層單元，通過改變實體單元彈性模量來建立考慮法向接觸剛度對裝配體振動模態影響的有限元模型。研究表明，不考慮法向接觸剛度的有限元整體模型解較解析解誤差很大，一般超過10%以上，且頻率越低差異越大;而考慮接觸剛度的有限元等效模型解與固有頻率解析解差異很小，即只要接觸剛度計算準確，本文提出的方法就能得到理想的計算結果，且計算簡單、實用。另外，考慮與不考慮接觸剛度，其各階模態振型也存在一定差異，這主要是接觸剛度單元的存在引起的。本文分析中假設了通過預載所形成的法向接觸剛度在振動中一直保持不變，事實上，由于在振動中接觸面間的接觸間隔一直在改變，所以接觸剛度也會跟著改變，這屬于非線性振動模態范疇，下一步將要進行深入研究。本文的研究，有助于分析像發動機盤式拉桿轉子這種連接剛度對系統振動模態影響較大的情況。

［1］施麗銘，張艷春.拉桿式模型轉子固有頻率的實驗與計算研究［J］.振動與沖擊，2008，27(S):47-49.

［2］王艾倫，駱 舟.拉桿轉子軸向振動的動力學模型［J］.中國機械工程，2009，20(13):1524-1527.

［3］章圣聰，王艾倫.盤式拉桿轉子的振動特性研究［J］.振動與沖擊，2009，28(4):117-120.

［4］ Zheng Y，Rong Y，Hou Z.A finite element analysis for stiffness of fixture units［J］.Journal of Manufacturing Science and Engineering，2005，127:429-432.

［5］高 銳，袁 奇，高 進.燃氣輪機拉桿轉子有限元模型研究及臨界轉速計算［J］.熱能動力工程，2009，24(3):305-308.

［6］饒柱石，夏松波.粗糙平面接觸剛度的研究［J］.機械強度，1994，16(2):71-75.

［7］約翰遜K J.接觸力學［M］.北京:高等教育出版社，1992.

［8］饒柱石.欄桿組合式特種轉子動力學特性及其接觸剛度的研究［D］.哈爾濱:哈爾濱工業大學，1992.

［9］Greenwood J A，Tripp J H.The contact of two nominally flat rough surface［J］.Pro.IMechE，1970，185:102-108.